69

Лекция 8

Расчет пропускной способности многозвенных схем методом вероятностных графов

1.Способы построения вероятностного графа

Метод вероятностных графов основывается на представлении коммутационной схемы в виде графа, конфигурация которого зависит от структуры схемы и режима искания, в котором используется схема. Вероятностный граф представляет собой картину всевозможных путей между заданным входом схемы и заданным выходом. При этом рассматривается не сама схема, а ее модель, в которой коммутаторы заменяются вершинами графа, а соединительные пути между коммутаторами – дугами графа.

Вероятностный граф может принадлежать к классу параллельно-последовательных графов или к классу непараллельно-последовательных графов.

Дальнейшая процедура метода вероятностных графов заключается в том, чтобы записать функцию потерь при установлении соединений в рассматриваемом графе между его входными и выходными полюсами, аргументом которой являются вероятности занятия отдельных дуг графа w_i . Для определения вероятности занятия дуг обычно используют значения средней интенсивности нагрузки, обслуженной каждой линией.

Рассмотрим построение коммутационных графов отдельных схем, работающих в различных режимах.

Д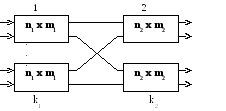вухзвенная схема

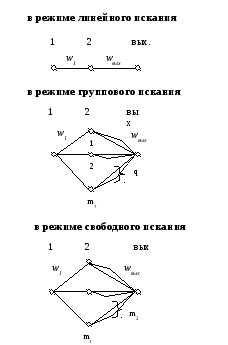
Трехзвенная схема

Как уже говорилось, вероятностный граф может быть двух типов: параллельно-последовательный и непараллельно-последовательный. Все графы, которые мы нарисовали, кроме последнего, параллельно-последовательные, а последний граф – непараллельно-последовательный.

Расчет вероятности потерь в параллельно-последовательном графе

Метод вероятностных графов основан на двух предположениях: независимость занятия всех последовательно включенных линий и независимости состояния всех линий, входящих в граф. Это предполагает большие размеры коммутаторов и большую вероятность блокировки для всех пучков линий.

Запись функции потерь для параллельно-последовательного графа сводится к умножению и суммированию вероятностей. При этом в случае параллельного включения нескольких дуг, образующих общую ветвь, для получения вероятности занятости всей ветви вычисляется произведение вероятностей занятия отдельных дуг.

Е

w₁

w_m

w₂

i

j

сли ветвь образуется последовательным включением дуг, то вероятность занятости всей ветви определится как дополнительная вероятность к вероятности свободности всей ветви, а вероятность свободности всей ветви, в свою очередь, определится как произведение вероятностей свободности отдельных последовательно включенных дуг.

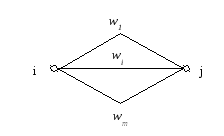
w₁ , w₂, …w_m – вероятности занятости дуг;

(1-w₁) , (1-w₂), …(1-w_m) –вероятности свободности дуг;

(1-w₁) (1-w₂)…(1-w_m) –вероятность свободности всей ветви;

-вероятность потерь. (2)

Вероятность потерь для параллельно-последовательного графа, состоящего из α параллельно включенных одинаковых ветвей, каждая из которых состоит из m дуг, запишется в виде:

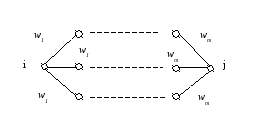
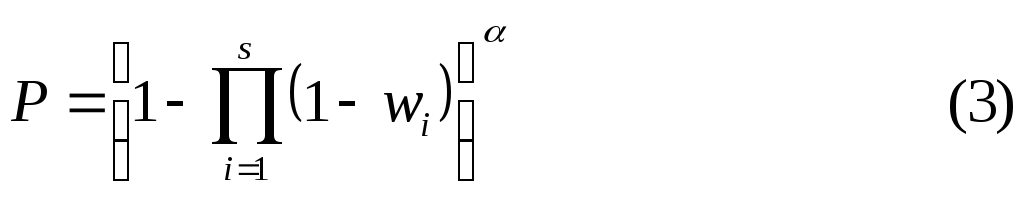
Выражения (1),(2),(3) являются основой для расчета любого параллельно последовательного графа.

Рассмотрим получение выражений для расчета потерь для составленных ранее графов.

Двухзвенная схема в режиме линейного искания

Звено А Звено В

а_вх

q=1

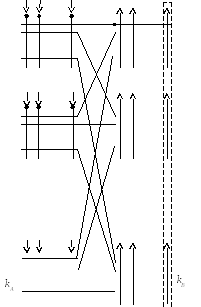n_A

1 1

m_A

2 2

- вероятность занятия промежуточной линии между звеньями А и В;

- вероятность занятия выхода.

Двухзвенная схема в режиме группового искания

Двухзвенная схема в режиме свободного искания

В справочной литературе предлагаются формулы для расчета потерь методом вероятностных графов для некоторых коммутационных схем, работающих в различных режимах искания.

Контрольные вопросы

1. Поясните сущность метода вероятностных графов для расчета пропускной способности многозвенных схем.

2. Что представляют собой вершины и дуги вероятностного графа многозвенной схемы?

3. От чего зависит вид вероятностного графа многозвенной схемы?

4. В чем заключается процедура расчета потерь по методу вероятностных графов после составления схемы графа?

5. Постройте вероятностный граф двухзвенной схемы в режиме группового искания.

6. Постройте вероятностный граф двухзвенной схемы в режиме свободного искания.

7. Постройте вероятностный граф трехзвенной схемы в режиме линейного искания.

8. Что является аргументом функции потерь при использовании метода вероятностных графов?

9. Запишите выражение функции потерь для случая параллельного включения нескольких дуг, образующих общую ветвь.

10. Запишите выражение функции потерь для случая последовательного включения нескольких дуг, образующих общую ветвь.

11. Запишите вероятность потерь для параллельно-последовательного графа, состоящего их α параллельно включенных одинаковых ветвей, каждая из которых состоит из m последовательно включенных дуг.

12. Запишите выражение вероятности потерь для двухзвенной схемы в режиме группового искания.

13. Запишите выражение вероятности потерь для двухзвенной схемы в режиме свободного искания.