Глава 4
.rtf
4.ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
-
Отделение корней. Пусть дано уравнение
|
f(x) = 0 , |
(1) |
где функция f (x) определена и непрерывна в некотором конечном или бесконечном интервале a < x < b.
Всякое значение , обращающее f (x) в 0, т.е. такое, что f () = 0, будем называть корнем уравнения (1) или нулем функции f (x).
Будем полагать, что уравнение (1) имеет только изолированные корни, т.е. у всякого корня существует окрестность, не содержащая других корней.
П р и м е р. Отделить корни уравнения
f(x) x3 - 6x + 2 = 0.
Р е ш е н и е. Функция определена всюду. Составим таблицу значений функции:
|
x |
- |
-3 |
-1 |
0 |
1 |
3 |
|
|
f(x) |
- |
-7 |
7 |
2 |
-3 |
11 |
|
Итак, уравнение имеет три вещественных корня в интервалах (-3;-1), (0;1), (1;3). Заметим, что если существует непрерывная производная f (x), и корни уравнения f (x) = 0 легко вычисляются, то проще найти знаки f (x) в точках нулей f (x) и в граничных точках x = a, x = b.
П р и м е р. Отделить корни уравнения
f(x) x 4 - 4x - 1 = 0.
Р е ш е н и е. Здесь f (x) = 4x 3 - 4. Следовательно, f (x) = 0 при x = 1. Имеем
|
x |
- |
1 |
|
|
f(x) |
|
-4 |
|
Таким образом, существуют два вещественных корня на промежутках (-; 1) и (1; ).
П р и м е р. Определить число вещественных корней уравнения
f(x) e x + x = 0.
Р е ш е н и е. Поскольку f (x) = e x + 1 и f (-) = -, f () = , то уравнение имеет только один вещественный корень.
-
Метод половинного деления. Пусть f(x) непрерывна на [a; b] и f(a)·f(b) < 0.
Имеем
уравнение f(x) = 0. Для нахождения корня
рассмотрим значение
.
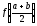Если
,
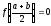то
является
корнем уравнения. В противном случае
выберем ту из половин
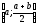или
,
в которой знаки f(x) противоположны на
концах. Получим отрезок [a1;
b1].
Продолжая процесс, получим бесконечную
последовательность вложенных отрезков
[a1;
b1],
…, [an;
b n],
таких, что f(a)·f(b) < 0 для любого
натурального n.
Очевидно, длина n-го отрезка
|
|
(2) |
Левые концы отрезков образуют монотонно неубывающую ограниченную последовательность a1, …, an , … Правые концы, соответственно, представляют монотонно невозрастающую ограниченную последовательность b1, …, b n , …
Тогда в силу (2) существует общий предел последовательностей an и b n при n .
Перейдем к пределу при n в неравенстве f(a)·f(b) < 0. В силу непрерывности f(x) получим [ f() ]2 0, следовательно, f() = 0, таким образом, - корень уравнения.
П р и м е р. Уточнить корень уравнения
f(x) x 4 + 2x3 - x - 1 = 0
на отрезке [0; 1] методом половинного деления.
Решение. Имеем a = 0, b = 1, f(a) = -1 < 0, f(b) = 1 > 0.
При первом делении отрезка получим
f (0.5) = - 19/16 < 0, т.е. [a1; b1] = [0.5; 1].
Таким образом, уточненный корень принадлежит интервалу (0.5; 1).
-
Метод хорд (пропорциональных частей). Пусть f(x) непрерывна на [a; b] и f(a)·f(b) < 0. Пусть также на [a;b] существует вторая производная f (x), причем знак f (x) остается постоянным на всем отрезке [a; b].
Положим для определенности f(a) < 0, f(b) > 0. Разделим отрезок [a; b] в отношении - f(a) : f(b). Геометрически это означает, что мы заменяем кривую f(x) на отрезке [a; b] хордой, проведенной через точки f(a), f(b). Такая хорда как раз и разбивает отрезок [a; b] в выбранном отношении. Точку разбиения внутри отрезка обозначим х1. Тогда получим
Продолжая процесс, применим тот же прием к тому из отрезков [a;х1] или [х1; b], на концах которого значения функции противоположны по знаку, и т.д.
Обобщим: для нахождения корня уравнения f(x) = 0 методом хорд необходимо:
-
Определить знаки f(a), f(b).
-
Определить знак f (x) на отрезке [a; b].
Далее, неподвижным будет тот конец отрезка, где знаки f (x) и f (x) совпадают.
Последовательные приближения корня уравнения располагаются по ту сторону от корня, где знаки f (x) и f (x) противоположны.
Таким образом, если неподвижный конец отрезка лежит в точке х=с, то х0 – противоположный конец отрезка. Далее последовательные приближения корня уравнения находим по формуле
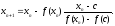
П р и м е р. Методом хорд уточнить корень уравнения
f(x) x3 – 0.2x2 – 0.2x – 1.2 = 0,
принадлежащий отрезку [1; 1.5 ].
Р е ш е н и е. Определим значения функции в концах отрезка:
f (1) = - 0.6 < 0, f (1.5) = 1.425 > 0.
Производная f (x) = 3x2 – 0.4x – 0.2 > 0 всюду на отрезке. Следовательно, внутри отрезка лежит ровно один корень уравнения.
Далее, f (x) = 6x – 0.4 > 0 также на всем отрезке. Следовательно, неподвижным концом отрезка будет х = 1.5, а в качестве начального приближения возьмем х0 = 1. Тогда, вычисляя последовательно, получим
х1 1.15, х2 1.19 и т. д.
(Заметим, что точным корнем уравнения на данном отрезке является х = 1.2.)
-
Метод Ньютона (метод касательных). Пусть корень уравнения f (x) = 0 отделен на отрезке [a; b], причем первая и вторая производные f (x) и f (x) непрерывны и сохраняют определенные знаки при a x b.
Пусть мы нашли некоторое n-е приближение корня
x n , x n [a;b].
Тогда мы можем уточнить его по методу Ньютона следующим образом.
Выберем в качестве начального приближения х0 тот конец отрезка, где знаки f (x) и f (x) совпадают.
Далее последовательные приближения корня уравнения находим по формуле
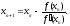
П р и м е р. Методом хорд уточнить корень уравнения
f(x) x 4 – 3x2 + 75x – 10000 = 0,
принадлежащий отрезку [-11; -10 ].
Р е ш е н и е. Определим значения функции в концах отрезка:
f (-11) = 3453 > 0, f (-10) = -1050 < 0.
Производная f (x) = 4x 3 – 6x + 75 < 0 всюду на отрезке. Следовательно, внутри отрезка лежит ровно один корень уравнения.
Далее, f (x) = 12x 2 – 6 > 0 также на всем отрезке. Таким образом, в качестве начального приближения выбираем х0 = -11. Тогда, вычисляя последовательно, получим
х1 -10.3, х2 -10.27 и т. д.
-
Метод итераций (метод последовательных приближений). Данное уравнение
|
f(x) = 0, |
(3) |
можно записать в виде равенства
x = (x),
выбирая различными способами функцию (x).
Для метода итераций выгодно такое представление (x), при котором выполнено неравенство
(x) q < 1.
Рассмотрим довольно общий прием приведения уравнения к требуемому в методе итераций виду.
Пусть искомый корень уравнения лежит на отрезке [a; b], причем
0 < m 1 f (x) M 1
при a x b.
(Замечание. Если производная f (x) отрицательна, то вместо уравнения f (x) = 0 будем рассматривать уравнение - f (x) = 0.)
В частности, за m1 можно взять наименьшее значение производной f (x) на отрезке [a; b], которое должно быть положительным, а за M 1 - наибольшее значение f (x) на отрезке [a; b]. Заменим уравнение (3) эквивалентным ему уравнением
x = x - f (x) ( > 0 ).
Можно положить (х) = x - f (x).
Подберем параметр таким образом, чтобы в данной окрестности [a; b] корня было выполнено неравенство
0 (x) = 1 - f (x) q < 1.
Отсюда получаем
0 1 - M 1 1 - m 1 q.
Следовательно, можно выбрать
= 1 / M 1 и q = 1 - m 1 / M 1 < 1.
П р и м е р. Найти наибольший положительный корень уравнения
x 3 + x = 1000
с точностью до четвертого знака.
Р е ш е н и е. Грубой прикидкой получаем приближенное значение корня х0 = 10, причем, очевидно, < х0.
Данное уравнение можно переписать в виде
x = (1000 – x ) 1/ 3.
Тогда, положив
(х) = (1000 – x ) 1/ 3,
будем иметь
. (х) -1 / 3 (1000 – x ) 2 / 3.
Отсюда
(x) 1/ 3 (990 ) 2 / 3 1 / 300 = q.
Вычисляем последовательные приближения с одним запасным знаком по формулам
y n = 1000 – х n ;
х n+1 = (y n ) 1/ 3 (n = 0, 1, 2, … ).
Найденные значения поместим в таблицу.
|
n |
х n |
y n |
|
0 |
10 |
990 |
|
1 |
9,96655 |
990.03345 |
|
2 |
9,96666 |
990.03334 |
|
3 |
9,96667 |
|
Поскольку 1 – q 1, то с точностью до четвертого знака можно положить = 9.9667.
ЗАДАЧИ
В задачах 1 – 27 определить число корней уравнения; отделить корни.
|
1. |
f(x) 2x3 - 6x + 3 = 0 |
2. |
f(x) x3 - 9x + 7 = 0 |
|
3. |
f(x) 8x3 - 6x + 1= 0 |
4. |
f(x) 6x3 - 4x + 1= 0 |
|
5. |
f(x) 3x3 - 6x2 + 2 = 0 |
6. |
f(x) 14x3 - 21x2 + 2 = 0 |
|
7. |
f(x) x3 + 3x2 - 3 = 0 |
8. |
f(x) 8x3 + 10x2 - 1 = 0 |
|
9. |
f(x) 2x3 - 6x + 1 = 0 |
10. |
f(x) x3 - 9x + 4 = 0 |
|
11. |
f(x) 20x3 - 15x + 2 = 0 |
12. |
f(x) 15x3 - 10x + 2 = 0 |
|
13. |
f(x) 2x3 - 4x2 + 1 = 0 |
14. |
f(x) 12x3 - 18x2 + 5 = 0 |
|
15. |
f(x) x3 + 3x2 - 1 = 0 |
16. |
f(x) 12x3 + 15x2 - 1 = 0 |
|
17. |
f(x) 9x3 - 9x2 + 1 = 0 |
18. |
f(x) x3 + 9x2 - 6 = 0 |
|
19. |
f(x) 3x3 + 6x2 - 2 = 0 |
20. |
f(x) 21x3 - 7x + 1 = 0 |
|
21. |
f(x) 2x3 - 8x + 5 = 0 |
22. |
f(x) - x3 + 15x - 12 = 0 |
|
23. |
f(x) - x3 + x – 0.25 = 0 |
24. |
f(x) 4x3 - 6x2 - 24x + 3 = 0 |
|
25. |
f(x) - 8x3 + 26x2 - 20x + 3 = 0 |
26. |
f(x) - 2x3 - 3x2 + 72x + 3 = 0 |
|
27. |
f(x) 5/3x3 - x2 - 3x + 2 = 0 |
|
|
В задачах 28 – 54 определить число корней; методом половинного деления найти корни уравнения с точностью до пятого знака.
|
28. |
f(x) 6x3 - 9x2 + 2.5 = 0 |
29. |
f(x) 0.5x3 + 1.5x2 – 0.5 = 0 |
|
30. |
f(x) 6x3 + 7.5x2 – 0.5 = 0 |
31. |
f(x) 4.5x3 – 4.5x2 + 0.5 = 0 |
|
32. |
f(x) 0.5x3 + 4.5x2 - 3 = 0 |
33. |
f(x) 1.5x3 + 3x2 - 1 = 0 |
|
34. |
f(x) 10.5x3 - 3.5x + 0.5 = 0 |
35. |
f(x) x3 - 4x + 2.5 = 0 |
|
36. |
f(x) - 0.5x3 + 7.5x - 6 = 0 |
37. |
f(x) - x3 + x – 0.25 = 0 |
|
38. |
f(x) 2x3 - 3x2 - 12x + 1.5 = 0 |
39. |
f(x) -4x3 + 13x2 - 10x + 1.5 = 0 |
|
40. |
f(x) - x3 – 1.5x2 + 36x + 1.5= 0 |
41. |
f(x) 5/6x3 – 0.5x2 – 1.5x + 1= 0 |
|
42. |
f(x) x3 - 3x + 1.5 = 0 |
43. |
f(x) 0.5x3 – 4.5x + 3.5 = 0 |
|
44. |
f(x) 4x3 - 3x + 0.5= 0 |
45. |
f(x) 3x3 - 2x + 0.5= 0 |
|
46. |
f(x) 1.5x3 - 3x2 + 1 = 0 |
47. |
f(x) 7x3 – 10.5x2 + 1 = 0 |
|
48. |
f(x) 0.5x3 + 1.5x2 – 1.5 = 0 |
49. |
f(x) 4x3 + 5x2 – 0.5 = 0 |
|
50. |
f(x) x3 - 3x + 0.5 = 0 |
51. |
f(x) 0.5x3 - 4.5x + 2 = 0 |
|
52. |
f(x) 10x3 - 7.5x + 1 = 0 |
53. |
f(x) 7.5x3 - 5x + 1 = 0 |
|
54. |
f(x) x3 - 2x2 + 0.5 = 0 |
|
|
В задачах 55 – 87 решить уравнения методом Ньютона; найти корни с точностью до третьего знака.
|
55. |
f(x) x3 - 5x + 1 = 0 |
56. |
f(x) x3 - 9x2 + 20x - 11 = 0 |
|
57. |
f(x) x3 - 3x2 - 3x + 11 = 0 |
58. |
f(x) x5 + 5x + 1 = 0 |
|
59. |
f(x) sin x + x - 1 = 0 |
60. |
f(x) x2 – 10 lg x – 3 = 0 |
|
61. |
f(x) 2x3 - 6x + 3 = 0 |
62. |
f(x) x3 - 9x + 7 = 0 |
|
63. |
f(x) 8x3 - 6x + 1= 0 |
64. |
f(x) 6x3 - 4x + 1= 0 |
|
65. |
f(x) 3x3 - 6x2 + 2 = 0 |
66. |
f(x) 14x3 - 21x2 + 2 = 0 |
|
67. |
f(x) x3 + 3x2 - 3 = 0 |
68. |
f(x) 8x3 + 10x2 - 1 = 0 |
|
69. |
f(x) 2x3 - 6x + 1 = 0 |
70. |
f(x) x3 - 9x + 4 = 0 |
|
71. |
f(x) 20x3 - 15x + 2 = 0 |
72. |
f(x) 15x3 - 10x + 2 = 0 |
|
73. |
f(x) 2x3 - 4x2 + 1 = 0 |
74. |
f(x) 12x3 - 18x2 + 5 = 0 |
|
75. |
f(x) x3 + 3x2 - 1 = 0 |
76. |
f(x) 12x3 + 15x2 - 1 = 0 |
|
77. |
f(x) 9x3 - 9x2 + 1 = 0 |
78. |
f(x) x3 + 9x2 - 6 = 0 |
|
79. |
f(x) 3x3 + 6x2 - 2 = 0 |
80. |
f(x) 21x3 - 7x + 1 = 0 |
|
81. |
f(x) 2x3 - 8x + 5 = 0 |
82. |
f(x) - x3 + 15x - 12 = 0 |
|
83. |
f(x) - x3 + x – 0.25 = 0 |
84. |
f(x) 4x3 - 6x2 - 24x + 3 = 0 |
|
85. |
f(x) - 8x3 + 26x2 - 20x + 3 = 0 |
86. |
f(x) - 2x3 - 3x2 + 72x + 3 = 0 |
|
87. |
f(x) 5/3x3 - x2 - 3x + 2 = 0 |
|
|
В задачах 88 – 114 найти корни уравнения методом хорд с точностью до пятого знака.
|
88. |
f(x) 4.5x3 + 9x2 - 1 = 0 |
89. |
f(x) 31.5x3 - 10.5x + 1.5 = 0 |
|
90. |
f(x) 3x3 - 12x + 7.5 = 0 |
91. |
f(x) - 1.5x3 + 22.5x - 18 = 0 |
|
92. |
f(x) - 1.5x3 + 1.5x – 0.375 = 0 |
93. |
f(x) 6x3 - 9x2 - 36x + 4.5 = 0 |
|
94. |
f(x) -12x3 + 39x2 - 30x +4.5=0 |
95. |
f(x) - 3x3 – 4.5x2+108x+4.5=0 |
|
96. |
f(x) 2.5x3 – 1.5x2 – 4.5x + 3=0 |
97. |
f(x) 3x3 - 9x + 4.5 = 0 |
|
98. |
f(x) 1.5x3 – 13.5x + 10.5 = 0 |
99. |
f(x) 12x3 - 9x + 1.5= 0 |
|
100. |
f(x) 9x3 - 6x + 1.5= 0 |
101. |
f(x) 4.5x3 - 9x2 + 3 = 0 |
|
102. |
f(x) 21x3 – 31.5x2 + 3 = 0 |
103. |
f(x) 1.5x3 + 4.5x2 – 4.5 = 0 |
|
104. |
f(x) 12x3 + 15x2 – 1.5 = 0 |
105. |
f(x) 3x3 - 9x + 1.5 = 0 |
|
106. |
f(x) 1.5x3 - 13.5x + 6 = 0 |
107. |
f(x) 30x3 - 22.5x + 3 = 0 |
|
108. |
f(x) 22.5x3 - 15x + 3 = 0 |
109. |
f(x) 3x3 - 6x2 + 1.5 = 0 |
|
110. |
f(x) 18x3 - 27x2 + 7.5 = 0 |
111. |
f(x) 1.5x3 + 4.5x2 – 1.5 = 0 |
|
112. |
f(x) 18x3 + 22.5x2 – 1.5 = 0 |
113. |
f(x) 13.5x3 – 13.5x2 + 1.5 = 0 |
|
114. |
f(x) 1.5x3 + 13.5x2 - 9 = 0 |
|
|
В задачах 115 – 162 решить уравнения методом итераций; найти значения корней с точностью до третьего знака.
|
115. |
f(x) x – (x + 1) - 2 = 0 |
116. |
f(x) x – (x + 1) 3 = 0 |
|
117. |
f(x) x–((x - 1)/(x + 1)) 1/ 3 -4=0 |
118. |
f(x) x – 2 x- 1/4 = 0 |
|
119. |
f(x) x – (5 - x) 1/ 3 = 0 |
120. |
f(x) x + tg x – 4 = 0 |
|
121. |
f(x) x 2 – sin x = 0 |
122. |
f(x) x 3 – sin x = 0 |
|
123. |
f(x) x – arcsin ((x + 1) / 4) =0 |
124. |
f(x) x - cos x = 0 |
|
125. |
f(x) x – (cos x) - 1 = 0 |
126. |
f(x) x – 1 – 0.1 sin x = 0 |
|
127. |
f(x) x ( lg (x + 2) 1/2 = 0 |
128. |
f(x) x 2 – ln (x + 1) = 0 |
|
129. |
f(x) x 2 + ln x - 4 = 0 |
130. |
f(x) x + ln x - 2 = 0 |
|
131. |
f(x) x 2 – e x - 2 = 0 |
132. |
f(x) 0.1x - lg x = 0 |
|
133. |
f(x) tg x - lg x = 0 |
134. |
f(x) x – 0.1e - x = 0 |
|
135. |
f(x) 2x3 - 6x + 3 = 0 |
136. |
f(x) x3 - 9x + 7 = 0 |
|
137. |
f(x) 8x3 - 6x + 1= 0 |
138. |
f(x) 6x3 - 4x + 1= 0 |
|
139. |
f(x) 3x3 - 6x2 + 2 = 0 |
140. |
f(x) 14x3 - 21x2 + 2 = 0 |
|
141. |
f(x) x3 + 3x2 - 3 = 0 |
142. |
f(x) 8x3 + 10x2 - 1 = 0 |
|
143. |
f(x) 2x3 - 6x + 1 = 0 |
144. |
f(x) x3 - 9x + 4 = 0 |
|
145. |
f(x) 20x3 - 15x + 2 = 0 |
146. |
f(x) 15x3 - 10x + 2 = 0 |
|
147. |
f(x) 2x3 - 4x2 + 1 = 0 |
148. |
f(x) 12x3 - 18x2 + 5 = 0 |
|
149. |
f(x) x3 + 3x2 - 1 = 0 |
150. |
f(x) 12x3 + 15x2 - 1 = 0 |
|
151. |
f(x) 9x3 - 9x2 + 1 = 0 |
152. |
f(x) x3 + 9x2 - 6 = 0 |
|
153. |
f(x) 3x3 + 6x2 - 2 = 0 |
154. |
f(x) 21x3 - 7x + 1 = 0 |
|
155. |
f(x) 2x3 - 8x + 5 = 0 |
156. |
f(x) - x3 + 15x - 12 = 0 |
|
157. |
f(x) - x3 + x – 0.25 = 0 |
158. |
f(x) 4x3 - 6x2 - 24x + 3 = 0 |
|
159. |
f(x) - 8x3 + 26x2 - 20x + 3 = 0 |
160. |
f(x) - 2x3 - 3x2 + 72x + 3 = 0 |
|
161. |
f(x) 5/3x3 - x2 - 3x + 2 = 0 |
162. |
f(x) 10x – 1 – cos x = 0 |