
Глава 8
.rtf8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Задача Коши для системы обыкновенных дифференциальных уравнений формулируется следующим образом:
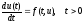 (1)
(1)
 (2)
(2)
где обозначено:
 -
вектор неизвестных;
-
вектор неизвестных;
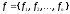 -
вектор правых частей уравнений.
-
вектор правых частей уравнений.
В задаче Коши по известному значению решения в точке t=0 необходимо найти решение при других t. Обычно в качестве аргумента t выступает время.
Для
нахождения приближенного решения задачи
(1),
(2)
наиболее часто используют метод
построения разностных схем, аппроксимирующих
данное дифференциальное уравнение. В
простых случаях используется равномерная
сетка по переменной t
с шагом h.
Будем обозначать
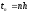 дискретные
значения аргумента,
дискретные
значения аргумента,
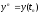 -
приближенное решение в узлах сетки.
-
приближенное решение в узлах сетки.
Метод
сходится в точке
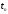 ,
если
,
если
 при
при
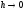 .
Метод имеет p-й
порядок точности, если
.
Метод имеет p-й
порядок точности, если
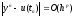 при
при
 .
.
Различают
явные и неявные методы. В явных методах
значение
 выражается явно через значения решения
в одной или нескольких предыдущих
точках, в неявных методах
выражается явно через значения решения
в одной или нескольких предыдущих
точках, в неявных методах
 определяется из неявного уравнения,
связывающего несколько соседних
значений.
определяется из неявного уравнения,
связывающего несколько соседних
значений.
-
Приближенное решение задачи Коши на основе разложения в ряд Тейлора. Предполагая, что решение u(t) и функция f(t, u) гладкие функции своих аргументов, разложим решение в ряд Тейлора в точке t = tn

Производные u выражаются через значение u и производные правой части с использованием уравнения (1). Например,

Ограничиваясь
несколькими первыми членами разложения
и заменяя
 приближенным значением
приближенным значением
 ,
получим рекуррентные формулы для
вычисления приближенного решения.
Например, ограничиваясь одним членом,
получим классический метод Эйлера
первого порядка
,
получим рекуррентные формулы для
вычисления приближенного решения.
Например, ограничиваясь одним членом,
получим классический метод Эйлера
первого порядка
 (3)
(3)
-
Методы Рунге-Кутта. Разностные схемы Рунге-Кутта строятся на основе метода “предиктор-корректор”, которую мы поясним на примере метода второго порядка. На первом шаге (предсказание) вычисляется предварительное значение приращения методом Эйлера. На следующем этапе (коррекция) приращение уточняется, при этом значение правой части уравнения вычисляется в средней точке шага, полученного на первом этапе. Итоговая схема выглядит так:
 (4)
(4)
Общая схема Рунге-Кутта использует большее количество промежуточных точек и имеет вид:
 (5)
(5)
Величины
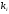 -
это оценки правой части, взятые в
различных промежуточных точках,
-
это оценки правой части, взятые в
различных промежуточных точках,
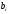 -
весовые коэффициенты, в сумме дающие
единицу. Выбор параметров
-
весовые коэффициенты, в сумме дающие
единицу. Выбор параметров
 определяет
вариант метода Рунге-Кутта. Если
определяет
вариант метода Рунге-Кутта. Если
 при
при ,
то имеем явный метод. Если
,
то имеем явный метод. Если
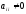 ,
то
,
то
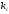 определяется
из неявного уравнения.
определяется
из неявного уравнения.
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка
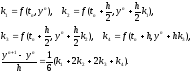 (6)
(6)
-
Методы Адамса. В методах Рунге-Кутта в вычислениях участвуют значения решения только в двух соседних узлах, что соответствует одному шагу по переменной t. В многошаговых методах используются уравнения, связывающие несколько соседних значений. Линейный m-шаговый метод записывается в виде
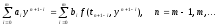 (7)
(7)
Вариант
численного метода определяется заданием
коэффициентов
 .
Для начала расчетов необходимо задать
m
начальных значений
.
Для начала расчетов необходимо задать
m
начальных значений
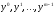 .
.
Различные варианты многошаговых методов (методы Адамса) могут быть получены на основе использования квадратурных формул для оценки интеграла в правой части равенства

Применяя
к подынтегральной функции интерполяционную
формулу по значениям
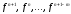 ,
получим неявный метод Адамса в форме
,
получим неявный метод Адамса в форме
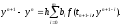 (8)
(8)
Для
получения явных многошаговых методов
можно использовать процедуру экстраполяции
подынтегральной функции по уже вычисленным
значениям
 ,
т.е.
,
т.е.
 (9)
(9)
Примерами явного и неявного методов Адамса являются, соответственно
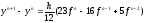 (10)
(10)
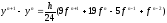 (11)
(11)
-
Устойчивость разностных схем. Исследование устойчивости используемых разностных схем при решении задачи Коши проводится чаще всего на модельном одномерном уравнении
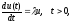 (12)
(12)
где
- комплексное число. Применение
конкретных численных методов к этому
уравнению дает линейную систему для
значений приближенного решения,
устойчивость которой оценивается по
корням характеристического уравнения.
Областью устойчивости называют множество
всех точек комплексной плоскости
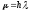 ,
для которых линейная система устойчива.
,
для которых линейная система устойчива.
Метод
называется A-устойчивым,
если область его устойчивости содержит
полуплоскость
 .
.
ЗАДАЧИ
-
Постройте метод приближенного решения задачи Коши
(1) - (2), используя разложение в ряд Тейлора и учитывая члены до второго порядка включительно.
2. Постройте метод приближенного решения задачи Коши
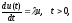
используя разложение в ряд Тейлора и учитывая члены до n-го порядка включительно.
3. Постройте метод приближенного решения задачи Коши

используя разложение в ряд Тейлора и учитывая члены до третьего порядка включительно.
4.
Постройте явный метод Рунге-Кутта
второго порядка при условии
 .
.
5. Получите условия устойчивости метода Эйлера первого порядка.
6. Получите условия устойчивости явного метода Рунге-Кутта второго порядка.
7. Получите условия устойчивости явного метода Рунге-Кутта четвертого порядка.
8. Постройте трехслойный метод решения задачи Коши, используя квадратурную формулу Симпсона для оценки интеграла.
9. Аппроксимируют ли задачу Коши следующие разностные схемы (хотя бы с первым порядком аппроксимации):
а)
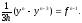
б)

в)

10. Для задачи

с точным решением u=t рассматривается схема

Каков порядок аппроксимации данной схемы, если
а)
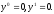
б)
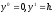
ОТВЕТЫ И РЕШЕНИЯ
1.
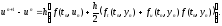
2.

3.

4. В силу общего представления (5) в рассматриваемом случае имеем

Оценим погрешность аппроксимации
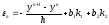 .
.
Разлагая это выражение в ряд Тейлора и приравнивая к нулю коэффициенты в разложении до второго порядка включительно, получим условия на коэффициенты метода второго порядка:

5.
Для
модельного уравнения с правой частью
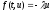
имеем

Метод
устойчив, если выполнено
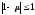 ,
т.е. область устойчивости представляет
собой окружность на комплексной плоскости
радиуса 1 с центром в точке –1.
,
т.е. область устойчивости представляет
собой окружность на комплексной плоскости
радиуса 1 с центром в точке –1.
6.
Для
модельного уравнения с правой частью

имеем
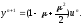
Метод
устойчив, если выполнено
 .
Для вещественных
область
устойчивости - отрезок от 0 до ½.
.
Для вещественных
область
устойчивости - отрезок от 0 до ½.
7.
Для
модельного уравнения с правой частью

имеем

Метод
устойчив, если выполнено
 .
Для вещественных
это
неравенство справедливо на отрезке от
0 до приблизительно 2.78.
.
Для вещественных
это
неравенство справедливо на отрезке от
0 до приблизительно 2.78.
8.
Интегрирование
уравнения (1) от
 до
до
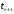 дает
дает
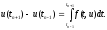
Используя
формулу Симпсона для правой части и
заменяя
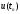 приближенным значением, получим метод
приближенным значением, получим метод
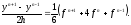
9. По формуле Тейлора имеем
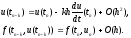
Подставляя
эти выражения, соответственно, в левые
и правые части разностных схем, получаем
условия, при которых равенства соблюдаются
при любых значениях
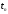 .
Проверка соблюдения этих условий для
приведенных примеров дает результат:
.
Проверка соблюдения этих условий для
приведенных примеров дает результат:
а) да; б) нет; в) да.
10. а) первый; б) второй.
