1.Проверка независимости

по предпочтению

2.Выбор вида ФЦ

3.Построение частных ФЦ

4.Нахождение шкалирующих

коэффициентов

5.Проверка согласованности

Рис.9

4.2 Функция полезности

Сразу обозначим область нашего дальнейшего анализа: это задача принятия решения (ЗПР) в условиях риска (в отличие от ФЦ, которая является ЗПР в условиях определенности). Более конкретно, мы переходим к рассмотрению следующей ЗПР:

Имеется совокупность альтернатив (действий) - a^,a, ... и совокупность исходов: x₁, .... x_n, причём исходы перенумерованы так, что x₁  x₂x₃ ... x_n, где  - символ бинарного отношения «хуже».

Если бы каждое действие приводило ко вполне определенному последствию (исходу), то проблема выбора наилучшего действия при наличии данной ранжировки исходов не стояла бы. Однако в наших условиях каждому действию а соответствует лишь определённое распределение вероятностей на множество исходов. Какое действие выбрать? Т.н. «классическая теория полезности», разработанная фон Нейманом и Моргенштерном, предлагает следующий путь:

Допустим, i ЛПР оценивает как эквивалентные 2 такие альтернативные возможности:

1.Получить x_i наверняка (т.е. с вероятностью 1).

2.Получить x_N (лучший исход) с вероятностью _i и x_i (худший) с вероятностью 1-_i,

т.е. мы каким то образом, на основе анализа систем предпочтений ЛПР подобрали такие значения _i. Если ЛПР действует разумно и последовательно (говорят, что его поведение является согласованным), то, очевидно _n=1, _i=0 и, кроме того,

₁  ₂  _n

Таким образом каждому исходу x_i поставлена в соответствие некоторая числовая оценка _i, называемая его полезностью.

Сравним теперь 2 альтернативы (действия) a и а, порождающие вероятности P_i и P_i соответственно на множестве исходов {x_i}. Подсчитаем величины:

и ,

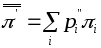которые естественно называть оценками ожидаемой полезности в случае выбора каждой из альтернатив. ТП утверждает, что следует выбрать ту альтернативу, у которой ожидаемая полезность - больше. Обоснование таково. Действия а^ эквивалентны представлению ЛПР шансов зах_n и шансов заx₁. Аналогично для а^.

Заметим также, что если преобразовать _i в u_i при помощи положительного линейного преобразования

u_i = a + b_i, b>0,

то

,

т.е. оценка u_i будет точно так же упорядочивать альтернативы по ожидаемой полезности. Если же сделать произвольное монотонное преобразование, то упорядочение нарушится, стало быть, полезность, в отличие от ценности, - есть качественный показатель и измеряется в шкале интервалов.

Теперь мы в состоянии дать определение ФП: это такая функция u(x), что u(x)=полезность x, x.

Важнейшими в теории полезности являются понятия монотонности, лотереи, детерминированного эквивалента.

Одномерная ФП монотонно возрастающая, если x₁>x₂  u(x₁) u(x₂).

Под лотереей в ТП понимается ситуация, в которой исход x₁ возможен с вероятностью p₁, x₂-p₂ и т.д.

Детерминированным эквивалентом лотереи называется величина такая, что ЛПР безразлично в выборе между участием в лотерее и получениемнаверняка. Заметим, что лотереи с двумя исходами уже были предметом нашего анализа.

Ожидаемый выигрыш в лотерее: .

Ожидаемая полезность лотереи: .

Определение.

ЛПР не склонен к риску, если предпочитает получить наверняка ожидаемый выигрыш в любой не вырождённой лотерее участию в этой лотерее:

. (4.1)

Теорема [2, с.149]. Принимающий решение не склонен к риску тогда и только тогда, когда его функция полезности вогнута.

Доказательство.

Необходимость.

Из (4.1) имеем: (для лотереи x₁-p, x₂-(1-p)).

u[px₁ + (1-p)x₂] > p(x₁) + (1-p)u(x₂), для 0<p<1,

что есть определение строгой вогнутости Иллюстрация этого положения представлена на рис.10.

u

Рис.10

Достаточность. (Доказательство справедливо при конечном числе исходов).

Рассмотрим произвольную лотерею х_i p_i, i = , где m - число исходов.

Тогда в силу вогнутости u()

,

что эквивалентно (4.1). (Условие х гарантируется выбором p_i).

Следствие. ЛПР, который предпочитает получение наверняка ожидаемого выигрыша любой лотереи 50-50 <х₁,х₂> участию в самой лотерее, не склонен к риску.

Определение. Две функции полезности u₁ и u₂ стратегически эквивалентны (u₁u₂) тогда и только тогда, когда они одинаково упорядочивают по предпочтительности любые две лотереи. Мы уже видели (когда формировали вывод о том, что полезность есть количественная характеристика и измеряется в шкале интервалов), что если u₁ = a+bu₂, то u₁u₂. Центральное значение в ТП имеет тот факт, что верно и обратное.

Теорема. [2., с.145]. Если u₁u₂ то a,b: u₁(х) = a + bu₂(x), x.

Доказательство

Пусть х[x^,x^*], причём х<x^*,,x^> (т.е. x^*- с вероятностью , x^- с вероятностью 1-). Эквивалентность установлена ЛПР. Отсюда:

u_i(x) = u_i (x^*) + (1-)u_i (x^), i = . (4.2)

Положим в этом равенстве i=2, и решим полученное уравнение относительно :

.

Подставив теперь полученное значение  в уравнение (4.2) при i=1:

и окончательно имеем

,

что и требовалось доказать.

Мы уже ответили на вопрос о целях построения ФП и её единственности. (по аналогии с тем, как это было сделано нами для ФЦ). Теперь обсудим, какими же свойствами должно обладать отношение предпочтений ЛПР, чтобы ФП существовала. Совокупность этих условий обычно называется аксиомами теории полезности. Они по-разному формируются различными авторами. В любом случае речь идёт о положениях, которые не могут быть доказаны математически внутри ТП, но могут быть в ряде случаев (возможно - косвенно) проверены экспериментально. Сформулируем эти аксиомы, следуя классической работе Льюса и Райфы [4].

Аксиома 1 Отношение предпочтения ЛПР (нестрогого) на множестве альтернатив полно.

Аксиома 2 (о приведении составных лотерей). Любая составная лотерея равноценна простой лотерее, имеющей исходы х₁,х₂, ... ,х_n, вероятность которых вычисляется согласно обычным правилам теории вероятности:

если L⁽ⁱ⁾ = (px₁, px₂, ....., px_n), i = [1,s],

то

(q₁L⁽¹⁾, q₂L⁽²⁾, ... , q_sL^(s))  (p₁x₁, p₂x₂, ... , p_nx_n), где

p_i= q₁p_i⁽¹⁾ + q₂p_i⁽²⁾ + ... + q_sp_i^(s).

Аксиома 3 (аксиома непрерывности).

Всякий исход х_i равноценен лотерее [(1-_i)x₁, _ix_n] (т.е.  соответствующее значение _i).

Аксиома 4 (аксиома эквивалентности). В любой лотерее входящий в неё с положительной вероятностью исход x_i можно заменить на эквивалентную ему лотерею [(1-_i)x₁, _ix_n].

Аксиома 5 (аксиома транзитивности). Отношение предпочтения на множестве альтернатив транзитивно.

Аксиома 6 (аксиома монотонности).

[px₁, (1-p)x_n] [px_1, (1-p^)x_n]  p^p.

В этих предположениях справедлива следующая теорема:

Если отношение нестрогого предпочтения ЛПР удовлетворяет аксиомам 1-6, то  числа u_i для исходов x_i: для двух лотерей L⁽¹⁾ L⁽²⁾ соотношение средних значений p_i⁽¹⁾u_i и p_i⁽²⁾u_i отражает предпочтительность лотерей.

Интересной модификацией рассмотренных нами соотношений является ситуация, в которой ЛПР обладает некоторым начальным уровнем (благосостояния) [8]. Обозначим его w₀. Введение этого параметра в анализ совершенно естественно: жизнь не начинается с нуля при принятии очередного решения и следует ожидать, что величина может повлиять на поведение ЛПР. Рассмотрим этот вопрос более подробно.

Напомним, что детерминированный эквивалент лотереи х^* мы определили соотношением:

.

Теперь это соотношение примет у нас такой вид:

.

Заметим, что w=w₀+x - это величина (важно, что не оценка!) благосостояния ЛПР после реализации лотереи, т.е. следствие этой лотереи. Поэтому и w^* целесообразно представить в виде:

w^*=w₀+p_a.

Что же такое p_a? Участие в лотерее для ЛПР эквивалентно получению w^* наверняка. w₀ у ЛПР уже есть (т.е. тоже наверняка!). Иначе говоря, возможность участия в лотерее увеличивает благосостояние ЛПР на p_a. Теперь ясно, что, если ЛПР будет предложено продать своё право на участие в лотерее, то минимальная цена, за которую ЛПР согласен это сделать, равна как раз p_a. Т.е. p_a - продажная цена лотереи. (отсюда и обозначение p_a = asking price).

Рассмотрим теперь противоположную ситуацию. Пусть ЛПР предлагают не продать, а купить право на участие в лотерее. Какую максимальную цену он будет готов заплатить? У нас уже есть схема получения ответа на этот вопрос. Результат покупки лотереи (разумеется, случайный) для ЛПР имеет вид:

w₀+x-p_b, (p_b - цена покупки=«bid price» лотереи).

Ожидаемая полезность этого результата должна быть как минимум не хуже (не меньше) полезности первоначального состояния w₀.

Получим:

.

Теперь поставим вопрос: как соотносится между собой р_a и р_b? Заметим, что при w₀=0 мы получим такие соотношения:

Как видно, даже в этом, казалось бы, простейшем случае не вполне ясно соотношение р_a и р_b, т.е. выполняется ли интуитивно привлекательное предположение о том, что

р_a>р_b.

Ответ на поставленный вопрос требует введения ряда новых понятий, к которым мы и переходим. Сейчас же лишь отметим, что возможно р_a<0. Это означает, что ЛПР готов доплачивать за то, чтобы не участвовать в лотерее (по смыслу такое поведение ЛПР эквивалентно страхованию). Если р_b<0, то величина р_b есть компенсация ЛПР за принимаемый на себя риск.

Для решения вопроса о соотношении p_a и p_b нам понадобится еще одно понятие, впервые появившееся в знаменитых работах К.Эрроу и Дж.Пратта 64-65 годов. Повторим их рассуждения. Исходным пунктом возьмем уже знакомое нам уравнение для определения эквивалента и цены продажи:

.

Попробуем решить это уравнение относительно p_a в общем виде, но приближенно, заменив выражение в левой и правой частях их аппроксимациями - разложениями в ряд Тейлора.

, где

=E(x) - (эта величина предполагается известной).

Для аппроксимации подынтегрального выражения в правой части воспользуемся разложением в ряд Тейлора до второго порядка. Целесообразность такой несимметричной трактовки левой и правой частей определяется тем, что отдельные значения х будут заметно больше отклоняться от , чем p_a от . Имеем:

• Подставим это выражение под интеграл в правой части. Учтем, что при этом:

Уравнение наше примет такой вид:

,

отсюда

или, вспомнив, что p_a- =  ( - премия за риск)

.

Выражение в квадратных скобках называется степенью абсолютной несклонности к риску (A_a). Отметим, что, если ЛПР нейтрален по отношению к риску (т.е. u - линейна), то A_a=0. A_a не меняется при произвольном линейном преобразовании функции полезности.

Теперь мы в состоянии доказать следующую теорему о соотношении p_a и p_b.

Теорема о p_a и p_b [8].

Если абсолютная несклонность к риску есть убывающая функция своего аргумента, то либо 0<p_b<p_a, либо 0>p_b>p_a.

Если абсолютная несклонность к риску есть возрастающая функция, то либо 0<p_a<p_b, либо 0>p_a>p_b.

Если абсолютная несклонность к риску = const, то p_a=p_b.

Доказательство:

1). Докажем, если p_а>0  p_b>0. Из определений p_a и p_b имеем:

При этом, с учетом того, что p_a и p_b являются неявными функциями от начального уровня благосостояния и лотереи, мы можем записать

Если p_а>0, то из возрастания функции полезности по своему аргументу следует

, а отсюда

.

Поскольку p_b зависит от распределения х и для всех х при вычислении математического ожидания в правой части принимает одно и то же значение, то последнее неравенство возможно только при p_b>0.

Лотерею в правой части уравнения (*) можно рассматривать как лотерею х для ЛПР с начальным уровнем благосостояния w₀-p_b(w₀,x). Запишем для нее уравнение для определения цены продажи.

.

Отсюда

.

Сопоставим и , в предположении, что . Как мы уже знаем, при этом , т.е. есть продажная цена лотереи х при начальном уровне благосостояния меньшем чем w₀. Если абсолютная несклонность к риску убывает, то

,

и таким образом

.

Другие части теоремы доказываются аналогично.

С концепцией компенсации за риск связано важнейшее для рассматриваемой нами теории понятие премии за риск. Формально определение таково. Премия за риск  есть:

 = E(x)-р_a,

т.е. разница между математическим ожиданием исхода и процентной ценой лотереи.

Справедлива следующая теорема о премии за риск.

Если функция полезности ЛПР монотонно возрастает и выпукла вверх (вниз), то премия за риск даже этого ЛПР в любой лотерее положительна (отрицательна).

Доказательство этой теоремы основывается на т.н. лемме Енсена, которую мы приведём здесь без доказательства (далее E[] - символ оператора математического ожидания):

Если y есть случайная переменная и f(y)- строго выпуклая вверх функция, то

Е[f(y)]<f(E[y]).

Если же f(y) выпукла вниз, знак неравенства меняется на противоположный, т.е. Е[f(y)]>f[E(y)].

Итак, пусть функция полезности ЛПР u() монотонно возрастает и выпукла вверх. Тогда из неравенства Енсена получим:

[u(w₀+x)]<u(E[w₀+x]) = u(w₀+E[x]).

Но для детерминированного эквивалента w^*

u(w^*)=E[u(w₀+x)],

отсюда

u(w*)<u(w₀+E[x]).

Поскольку u() монотонно возрастает, последнее возможно только при условии, что

w^*<w₀+E[x],

т.е. w^*-w⁰<E[x].

w^*=w⁰-p_a,

p_a<E[x],

т.е. >0.

Изучим теперь вопрос о том, чем определяется вид (или тип) функции полезности. Изложение будем вести на примере двухфакторных функций полезности. Обобщение на случай большого числа факторов очевидно.

Пусть 2 фактора y⁰yy^* и z⁰zz^*. Найдём для лотереи 50-50 вида (y₁,z⁰),(y₂,z⁰) детерминированный эквивалент вида (,z⁰). Если при этом не зависит отz⁰ (а зависит только от y₁ и y₂), то говорят, что у не зависит по полезности от z.

Иначе говоря, условные функции полезности u (,z⁰) и u(,z) стратегически эквивалентны. Из доказанной нами теоремы следует, что

u(y, z) = g(z) + h(z)u(y,z⁰). (4.3)

Это соотношение является ключевым для доказательства следующего положения о виде ФП:

Теорема [2., c.225]. Если Y и Z взаимонезависимы по полезности, то ФП от двух аргументовY и Z является полилинейной, т.е. может быть представлена в виде

u(y, z) = u(y,z⁰) + ku(y,z⁰)u(y⁰,z)

или

u(y, z) = k_yu_y(y) + k_zu_z(z) + k_yzu_y(y)u₂(z),

где

1) u(y⁰,z⁰)=0, u(y^*, z^*) =1.

2) u_y(y⁰)=0, u_y(y^*)=1.

u(z⁰)=0, u_z(z*)=1.

3) k_y+k_z+k_yz=1.

Доказательство.

Из (4.3) при y=y⁰ получим: u(y⁰,z)=g(z)+h(z) u(y⁰,z⁰) т.е. u(y⁰,z)=g(z)

Поскольку g(z) и h(z) параметрически зависят от Z⁰ и НЕ зависят от у, то полученное выражение для g(z) можно использовать для вычисления u(y¹,z), где y¹y⁰:

u(y¹,z)= u(y⁰,z)+h(z)u(y¹,z⁰).

Отсюда получим

.

Подставляя теперь выражение для g(z) и h(z) в (4.3), получим:

.

Аналогично может быть получено симметричное выражение (исходя теперь из предположения, что Z не зависит по полезности от Y)

.

Используем последнее уравнение для вычисления u(y¹,z), входящего в предшествующее, и подставим его туда:

т.е. мы получим первое из требуемых представлений u(y,z) Введём теперь функции u_y() и u_z() в соответствии со следующими условиями:

и определим

.

Получим второе требуемое представление для u(y,z). Доказательство (3)-го условия теоремы получается прямой подставкой в только что полученное представление для u(z,y) значений y=y^* и z=z^*.