IV. Построение объединенной модели авторегрессии – скользящего среднего (арисс) rem: см. Приложение4 Для исследования арисс – модели рассмотрим частные случаи.

1. Модель авторегрессии (АР – модель порядка р) с основным уравнением:

y_t = a₁* y_t-1 + a₂ * y_t-2 + … + a_р * yt_-p + _t,

или можно воспользоваться введением оператора сдвига В

(В) y_t = _t,

где (В) = 1 – а₁В – а₂В² - … - а_рВ^р.

2. Модель скользящего среднего, или СС-модель, порядка q, основное уравнение которой имеет вид:

у_t = _t – b₁*_t-1 – b₂*_t-2 – … - b_q*_t-q

где _t – случайная величина, имеющая нормальное распределение, М(_t) = 0, D(_t) = . Поскольку _t не меняется со временем и не вносит дополнительной информации в описание процесса, она носит название белого шума.

Определим оператор скользящего среднего:

(В) = 1 – b₁В – b₂В² - … - b_qВ^q, тогда СС - модель можно записать в виде:

у_t =(В)*_t, где параметры b₁, b₂, … ,b_q и должны быть оценены на основе выборочных наблюдений ( min).

3. Смешанная модель авторегрессии и скользящего среднего (АРСС – модель).

Применяется в описании стационарного процесса авторегрессии для представления остатка в виде скользящего среднего:

(В) y_t =(В) _t.

В модели используется (p+q+2) параметров: р параметров авторегрессии, q параметров скользящего среднего, среднее значение показателя y_t и дисперсия ”белого шума”_t.

4. Объединенная (интегрированная) модель авторегрессии и скользящего среднего (АРИСС – модель).

Данная модель формируется за счет включения в АРСС – модель оператора взятия конечных разностей показателя y_t . Общая формула АРИСС – модели имеет вид:

(В)(1-В)^d y_t =(В) _t, где d – порядок разности.

АРИСС – модель имеет порядок (p,d,q).

Таким образом, АРИСС – модель может рассматриваться в следующих в частных случаях:

при (р,0,q) – смешанная модель;

при (р,0,0) – модель авторегрессии;

при (0,0,d) – модель скользящего среднего.

Определим порядок авторегрессионной составляющей.

Для начала определим порядок d оператора перехода к конечным разностям.

Рассчитаем выражение и определимd, при котором оно будет минимальным.

Проведенные расчеты для d = 0,1,…,8 показали, что минимальное значение выражение принимает при d = 1.

d	Sz
0	17.505
1	2.327
2	4.376
3	8.238
4	15.593
5	29.928
6	58.12
7	113.851
8	223.021

Определим параметры авторегрессии а₁, а₂, … а_р по методу Юла – Уокера.

Параметры определяются из решения системы:

Откуда получаем, что для авторегрессии первого порядка

а₁ = r₁,

для авторегрессии второго порядка

Далее следует рассмотреть процесс скользящего среднего и определить его параметры.

Для случая q = 1модель имеет вид

y_t = (1 – b₁B)_t , выражая величину_t черезy_t , получим

_t = (1 – b₁B) y_t = y_t + b₁ y_t-1 + b₂ y_t-2 + …

Таким образом, значение y_t в модели скользящего среднего зависит от бесконечного ряда своих лаговых значений:

y_t = =_t - b₁ y_t-1 - b₂ y_t-2 - …

Данный ряд сходится при |b₁| < 1. В этом случае модель скользящего среднего называется обратимой. Условие обратимости не зависит от условия стационарности рядаy_t .

В общем случае если у_t =(В)*_t, то условие обратимости состоит в возможности восстановления значений_t по значениям у_t.

Для вычисления автокорреляционной функции СС рассмотрим его ковариацию:

_k = E[у_tу_t-k] = E[(_t – b₁*_t-1 – b₂*_t-2 – … - b_q*_t-q)(_t-k – b₁*_t-k-1 – b₂*_t-k-2 – … - b_q*_t-k-q)].

Учитывая, что E[_t_t-k] = 0, приk  0, получаем дисперсию процесса, равную

_о = (1 + b₁² + b₂² + … + b_q²)_t².

Автоковариация k-того порядка выражается формулой

_k =

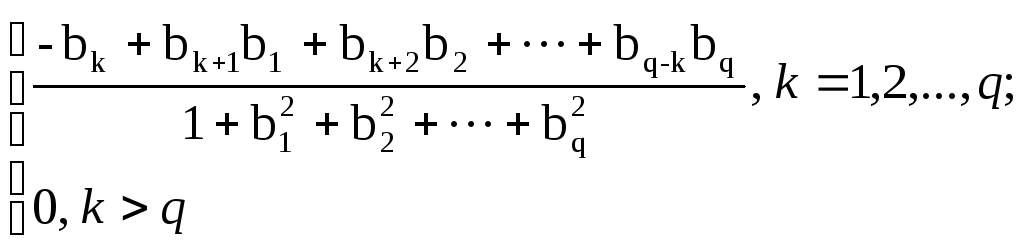
Снова рассмотрим процесс СС первого порядкаy_t = (1 – b₁B)_t, условие обратимости –1< b₁ < 1, дисперсия процесса_о = (1 + b₁²)_t² .

Значение автокорреляционной функции 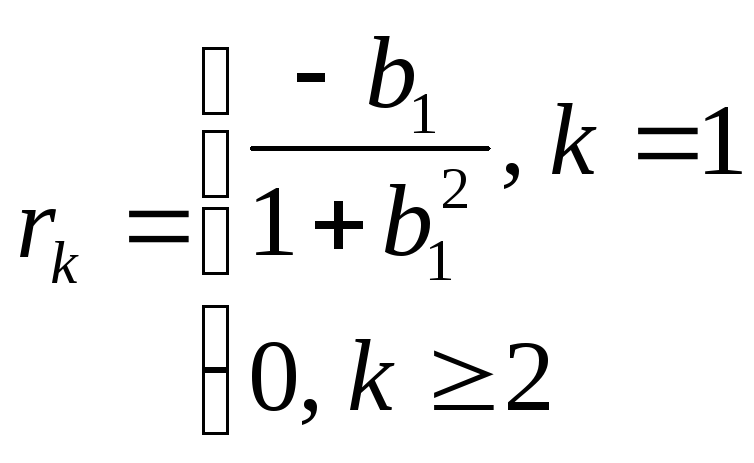, откудаb₁ может быть получен как результат решения квадратного уравнения (корень, для которого выполняется условие обратимости)

Аналогично, для процесса СС 2-го порядка можно получить следующие автокорреляционные функции и из них вычислить значения параметров, удовлетворяющих условиям обратимости b₁ + b₂ >1, b₂ - b₁ < 1, -1 < b₂ < 1:

.

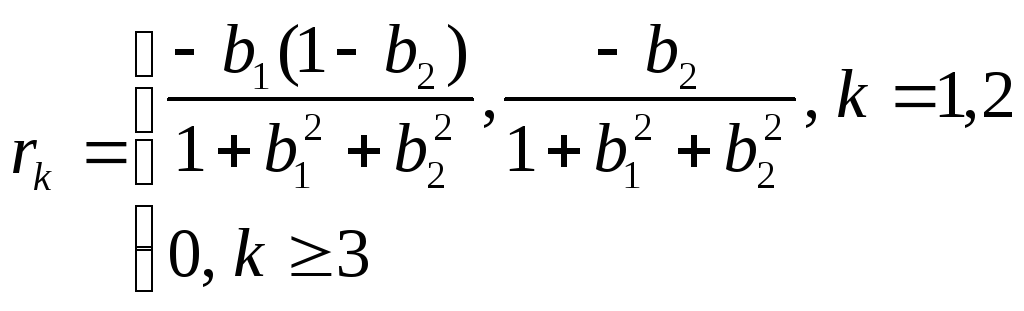Проанализируем возможные АРИСС (p,1,q) модели с целью выбора оптимальных параметровp иq, а затем проверим прогностические способности выбранных моделей с целью выбора лучшей для построения дальнейшего прогноза.

Значения коэффициентов АРИСС(р,1,d)

параметры	значения	sa	tкр	t(0.05,29-p-q-2-1)
AR(1) уt среднее константа t strd	-0.84 2.0 3.69 1.5	0.14 0.16	-6.09 12.7	2.06
AR(1) AR(2) уt среднее константа t strd	-1.28 -0.58 2.01 5.75 1.32	0.185 0.19 0.09	-6.86 -3.05 22.08	2.06
AR(1) AR(2) AR(3) уt среднее константа t strd	-1.37 -0.82 -0.22 2.01 6.86 1.32	0.21 0.31 0.22 0.08	-6.51 -2.64 -0.98 25.85	2.07
AR(1) AR(2) AR(3) AR(4) уt среднее константа t strd	-1.48 -1.3 -1.08 -0.68 2.0 11.09 1.099	0.17 0.28 0.28 0.18 0.04	-8.5 -4.6 -3.8 -3.8 49.4	2.07
AR(1) AR(2) AR(3) AR(4) AR(5) уt среднее константа t strd	-1.63 -1.52 -1.38 -1.08 -0.32 2.01 13.92 1.098	0.22 0.35 0.37 0.34 0.22 0.03	-7.33 -4.33 -3.75 -3.17 -1.44 61.13	2.08
AR(1) МА(1) уt среднее константа t strd	-0.7 0.89 2.02 3.43 1.10	0.17 0.08 0.02	-4.13 10.83 86.7	2.06
AR(1) AR(2) МА(1) уt среднее константа t strd	-0.92 -0.34 0.89 2.02 4.57 1.07	0.21 0.21 0.05 0.02	-4.38 -1.62 17.4 127.5	2.07
AR(1) AR(2) AR(3) AR(4) МА(1) уt среднее константа t strd	-1.1 -0.71 -0.72 -0.57 0.87 2.02 8.28 0.94	0.19 0.25 0.25 0.18 0.35 0.01	-5.76 -2.8 -2.9 -3.23 24.68 239.6	2.08
AR(1) МА(1) МА(2) уt среднее константа t strd	-0.44 1.71 -0.74 2.02 2.92 0.93	0.2 0.03 0.03 0.006	-2.2 56.3 -26.5 350.3	2.07
AR(1) AR(2) AR(3) AR(4) МА(1) МА(2) уt среднее константа t strd	-0.63 -0.22 -0.5 0.5 1.57 -0.62 2.02 5.75 0.92	0.23 0.19 0.22 0.23 0.2 0.17 0.005	-2.74 -1.12 -2.32 -2.18 8 -3.68 417	2.09
AR(1) МА(1) МА(2) МА(3) уt среднее константа t strd	-0.74 1.33 -0.07 -0.3 2.02 3.51 0.95	0.32 0.32 0.65 0.33 0.007	-2.27 4.12 -0.11 -0.89 310.5	2.07

На основе приведенных расчетов выберем по критерию минимума стандартизированной дисперсии «белого шума» _t strdтри модели: АРИСС(1,1,1), АРИСС(1,1,2) и АРИСС(4,1,1), и проведем для них оценку прогностических способностей с целью выбора лучшей для построения прогноза на 31 период.

Вид модели	КТейла	t strd
АРИСС(1,1,1)	0.019	1.10
АРИСС(1,1,2)	0.023	0.93
АРИСС(4,1,1)	0.021	0.94

Таким образом, учитывая специфику АРИСС-модели выберем для построения прогноза АРИСС(4,1,1).

Перестроив модель по 30 данным получим следующие параметры:

параметры	значения	sa	tкр	t(0.05,29-p-q-2-1)
AR(1) AR(2) AR(3) AR(4) МА(1) уt среднее константа t strd	-1.03 -0.77 -0.73 -0.48 0.88 2.017 8.1 0.95	0.19 0.26 0.27 0.18 0.08 0.008	-5.5 -2.94 -2.76 -2.63 11.48 241.1	2.07

Построение прогноза по АРИСС – модели.

Прогнозирование осуществляется с помощью формулы АРИСС-модели (в общем виде):

(В)(1-В)^d y_t =(В)_t.

Предсказываемый уровень выражается в виде:

y^*_t+l = a₁y_t+l-1 + a₂y_t+l-2 + … + a_py_t+l-p +_t+l – b₁_t+l-1 - … - b_q_t+l-q.

С другой стороны, для предсказания y_t+l может быть использована бесконечная линейная комбинация _t:

y^*_t+l = ’_l_t + ’_{l +1}_t-1 +’_{l +2}_t-2 + …

Дисперсия ошибки прогноза:

Е[y_t+1-y^_t+1]² = (1+²₁+…+²_l-1)²_t + {_l+j-^_l+j}²²_t.

Минимум достигается только при _l+j = ^_l+j.

Будущее значение y_t+1 = е_t+l + y^*_t+l , причем fhdjgj Е(е_t+l) = 0 (предсказанное значение y^*_t+l является несмещенной оценкой y_t+1),

а D(е_t+l) =(1+²₁+…+²_l-1)²_t.

При известных коэффициентах АРИСС-модели величины _j могут быть получены путем приравнивания коэффициентов с одинаковыми степенями В (из характеристических уравнений):

₁ = a₁ – b₁

₂ = a₁₁ + a₂ – b₂

_…

_j = a₁_j-1 + … +a_p+1_j-p-d – b_j,

где ₀ = 1, _j = 0 для j < 0иb_j =0 для j>q.

Если j>max{p-d-1,q}, то_j удовлетворяет уравнению вида

_j = a₁_j-1 + … +a_p+1_j-p-d и определяется с помощью рекурсивных формул.

Задавая уровни значимости можно определить и интервальные границы прогноза:

y_t+l = y^_t+l u_a/2{1+}^1/2²_t, гдеu_a/2 – квантиль нормального распределения.