4. Комплексное представление сигналов

При изучении гармонических сигналов широко пользуются символическим методом, заменяя действительный сигнал комплексной функцией.

Величину называют сопряженным сигналом. Два сигналаисвязаны между собой линейными интегральными преобразованиями, называемымипреобразованиями Гильберта.

Если определяется таким образом, то комплексный сигнал называют аналитическим сигналом (гильбертовский сигнал).

Все сказанное можно распространить и на случайные процессы. Ансамбль комплексных функций действительной переменной t, представляет собой комплексный случайный процесс.

Математическое ожидание комплексного случайного процесса

.

Дисперсия

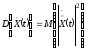
Здесь - центрированный процесс.

Функция корреляции комплексного процесса определяется следующим образом:

,

где * означает комплексно-сопряженную величину.

В дальнейшем будем говорить только об аналитических комплексных случайных процессах, в которых .

Представим аналитический случайный сигнал в экспоненциальной форме:

,

где

- действительный неотрицательный случайный процесс, называемый огибающей сигнала X(t); - фаза сигнала.

Введем величину Ф(t)= 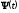- - мгновенная начальная фаза.

Действительный сигнал и сопряженный с ним можно представить в квазигармонической форме.

5. Теорема Котельникова

Функцию x(t) с финитным спектром можно точно восстановить по ее отсчетам , взятым через интервалы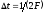, где F - верхняя частота спектра функции.

Это осуществляется с помощью ряда

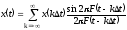. (1)

В соответствии с этой теоремой, функцию x(t), заданную на непрерывной оси времени, можно представить с помощью последовательности , заданной на дискретных точках.

Функции

(2)

образуют ортогональный базис в пространстве сигналов с финитным энергетическим спектром, т.е. таких, для которых

G(f)=0 при |f|>F. (3)

Функции 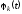называют функциями отсчета. Функцииотличаются друг от друга только сдвигами по времени на интервалы, кратные. Т.е. при t=n, где n-любое целое число, все функции отсчета, кроме, равны нулю, а=1.

Эту теорему можно обобщить и на случайные процессы.

Строгая формулировка теоремы Котельникова такова :

Для случайного процесса X(t) с энергетическим спектром , удовлетворяющим условию (3), ряд,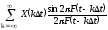

где 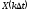- случайные отсчеты процесса X(t), взятые через интервалы, сходится к процессу X(t).

Основное значение этой теоремы заключается в том, что она позволяет в многих случаях заменить изучение случайного процесса X(t), заданного на непрерывной оси времени, изучением случайной последовательности .

Равенство (3) остается справедливым, если вместо верхней частоты спектра F взять любую частоту . Следовательно, ряд Котельникова можно записать и для.

Чтобы избавиться от F в формуле для ряда Котельникова, запишем

.

Представление непрерывного сигнала x(t) с помощью дискретных отсчетов называетсядискретизацией.

Котельников доказал также аналогичную теорему для полосовых сигналов, т.е. таких, спектр которых заключен между частотами

и , т.е.при |f|<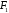и при |f|>.

В соответствии с этой теоремой такая функция может быть однозначно восстановлена по ее отсчетам , взятым через интервалы времени.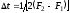

На практике часто приходится встречаться с сигналами, энергия которых почти полностью сосредоточена на интервале времени от дои в полосе частот от -F до F. Из теории преобразований Фурье известно, что финитный (во времени) сигнал не может иметь финитный спектр. Однако слово “почти” оправдывает рассмотрение таких сигналов и позволяет представлять их не бесконечным рядом Котельникова, а конечной суммой.

Будем полагать, что вся энергия сигнала x(t) содержится в полосе частот |f|<F, а все отсчеты за пределами интервала (,) равны нулю.

. (4)

Величину B=2FT называют базой сигнала.

Вопросы.

1) Случайная последовательность представляет собой цепь Маркова. Зависит лиот? Зависит лиот?

2) X(t) и Y(t) - два независимых стационарных процесса с ФК. Чему равны ФК процессов Z(t)=X(t)+Y(t), U(t)=X(t)-Y(t) и ?

3) При тех же условиях выразите спектральные плотности процессов Z(t), U(t) и V(t) через спектральные плотности ипроцессов X(t) и Y(t).

4) Докажите, что функции попарно ортогональны, т.е. при nk.

5) Чему равен интервал 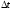в ряде Котельникова для сообщения телеметрической системы, в котором максимальная частота F=10Гц? Для телевизионного сообщения с F=6Mгц?

6) Чему равна база сигнала, соответствующего одному телевизионному кадру, который длится 1/25 c, если ширина его спектра 6Мгц?