Общая_Теория_Связи_Лекции / lex_8

4

Лекция № 8 по курсу

“Теория электрической связи”

ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ

1. Дискретные сигналы

Дискретные сигналы начали использовать ещё в 40-х годах при создании РТС с импульсной модуляцией. Этот вид модуляции отличается тем, что в качестве несущего колебания вместо гармонического сигнала служит периодическая последовательность коротких импульсов.

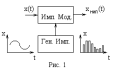
На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, соответствующую отсчетному значению аналогового сигнала. Сигнал х_МИП(t) на выходе из модулированной импульсной последовательности

Математическую модель идеальной МИП можно получить следующим образом. Рассмотрим формулу динамического представления сигнала:

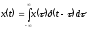
Поскольку МИП определена лишь в точках t_k = k (k = 0,1,2,...), интегрирование следует заменить по индексу k. Роль дифференциала d будет играть интервал дискретизации . Тогда математическая модель МИП, образованной бесконечно короткими импульсами:

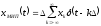, (1)

где - выборочные значения аналогового сигнала.

Исследуем сигнал в виде МИП. Если дискретизирующая последовательность имеет вид

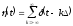, то сигнал вида МИП (2)

Спектр преобразования двух сигналов ~ свёртке их спектральных плотностей. Тогда

(3)

Для того, чтобы найти спектральную плотность дискретизирующей последовательности, разложим функцию (t) в ряд Фурье:

Коэффициенты этого ряда : .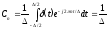

Тогда

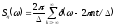(4).

Т.е. спектр дискретизирующей последовательности состоит из бесконечной совокупности дельта импульсов.

Подставив (4) в (3), находим:

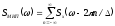(5)

Т.е. спектр сигнала, полученного в результате идеальной дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа “копий” спектра исходного аналогового сигнала.

2. Дискретное преобразование Фурье

Воспользуемся моделью в виде последовательности дельта импульсов и сопоставим исходному колебанию x(t) его дискретное МИП - преобразование.

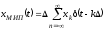
С коэффициентами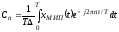

Подставляя выражение для х_МИП и вводя безразмерную переменную = t/, получим:

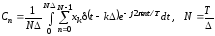
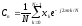(6)

Формула (6) определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ).

Свойства ДПФ.

1. ДПФ есть линейное преобразование.

2. Коэффициент С₀ (постоянная составляющая) является средним значением всех отсчетов

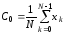
3. Если отсчетные значения x_k - вещественные числа, тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряженные пары. .

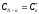Предположим, что коэффициенты С_n, образующие ДПФ, заданы для того, чтобы вычислить отсчетные значения, используют обратное дискретное преобразование Фурье:

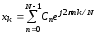(7)

3. Теория z - преобразований.

Пусть {x_k} = {x₀,x₁,x₂,...} - числовая последовательность, содержащая отсчетные значения некоторого сигнала. Поставим ей в однозначное соответствие сумму ряда по отрицательным степеням комплексной переменной z:

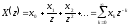(8)

Эта сумма называется z - преобразованием последовательности {x_k} использование z - преобразования позволяет изучать дискретные сигналы методами математического анализа непрерывных функций.

На основании формулы (8) можно непосредственно найти z - преобразование дискретных сигналов с конечным числом отсчетов. Так, простейшему дискретному сигналу с единственным отсчетом {x_k} = {1,0,0,...} соответствует X(z) = 1. Если же, например, {x_k} = {1,1,1,0,0,0,...}, то

.

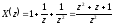Полагая, что отсчеты {x_k} есть значения непрерывной функции x(t) в точках t = k, любому сигналу x(t) можно сопоставить его z - преобразование при выбранном шаге дискретизации:

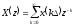(9)

Например, если x(t) = exp(t), то соответствующее z - преобразование:

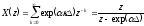
Если в формуле (9) положить z = exp(jw), то выражение

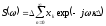(10)

будет преобразованием Фурье.

Свойства z - преобразования.

1. Линейность. Если {x_k} и {y_k} - дискретные сигналы, причем известны соответствующие z - преобразования X(z) и Y(z), то сигналу {u_k} = {x_k + y_k} будет отвечать преобразование U(z) = X(z) + Y(z) при любых постоянных и .

2. z - преобразование смещенного сигнала. Рассмотрим дискретный сигнал {y_k}, получающийся из дискретного сигнала {x_k} путем сдвига на одну позицию в сторону запаздыванья, т.е. когда y_k = x_k-1 (11)

Таким образом, символ z^-1 служит оператором единичной задержки (на один интервал дискретизации)

3. z - преобразование свертки. Пусть x(t) и y(t) - непрерывные сигналы, для которых определена свертка:

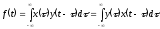
Применительно к дискретным сигналам принято вводить дискретную свертку {f_k}

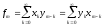, m = 0,.1,2,... (12)

Вычислим z - преобразование дискретной свертки:

Итак, свертке двух дискретных сигналов отвечает произведение z - преобразований.