2. Пространство сигналов

Рассмотрим два сигнала, заданных на интервале времени (0,Т) и имеющих вид , где, k - постоянное число,- может принимать любые неотрицательные значения, а- любые значения на интервале (0,). Эти сигналы представляют собой синусоиды одной и той же частоты, но с разными амплитудами и начальным фазами. Будем изображать каждый из этих сигналов вектором на плоскости с прямоугольными координатами XY, и имеющим длинуи направленный под углом относительно оси X.

Расстоянием между векторами будем называть расстояние d между их концами. Как известно из тригонометрии, .

Здесь 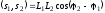- скалярное произведение векторови. Т.о., с увеличением скалярного произведения векторов расстояние между ними уменьшается.

Скалярное произведение совпадает с интегралом от произведения сигналов:

Помеха, добавляющая к сигналу, смещает конец соответствующего ему вектора. Поэтому, чем меньше расстояние между двумя векторами, тем вероятнее, что помеха приведет к невозможности уверенно отличать один сигнал от другого, что является причиной ошибочного приема переданного сигнала.

Если же рассматриваются более сложные ансамбли сигналов, то используются пространства более высоких порядков (4-х, 3-х мерные). Поэтому для изучения теории передачи сигналов необходимо иметь общее представление об основах функционального анализа.

В функциональном анализе множество любых элементов x,y,... называется линейным пространством, если оно удовлетворяет следующим условиям:

1. Для любых двух элементов x и y однозначно определен третий элемент x+y, называемый их суммой и также входящий в данное пространство, причем x+y= y+x; x+(y+z)=(x+y)+z.

2. В линейном пространстве существует нулевой элемент, обозначенный 0, такой, что x+0=x для всех х.

3. Для каждого элемента х линейного пространства существует противоположный ему элемент (-х), такой, что х+(-х)=0.

4. Любой элемент пространства можно умножить на любое число из некоторого множества {}, которое называется множеством скаляров,

.

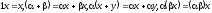Нормой вектора х называется неотрицательное число, обозначаемое и равное арифметическому значению.

Расстоянием между векторами x и y называют норму разности этих векторов:

Неравенство Коши-Буняковского-Шварца

.

Длина стороны треугольника меньше суммы длин двух других сторон (соотношение треугольника).

Если (x,y)=0, то и элементы пространства x и y называютсяортогональными.

Подмножество векторов называется ортогональной системой, еслипри kn.

В любом n-мерном пространстве можно построить полный ортогональный базис, т.е. систему из n ортогональных векторов.

Ортогональный базис, удовлетворяющий условию

называется ортонормированным.

Ортогональный базис в линейном пространстве определяет некоторую систему декартовых координат. Каждый вектор можно представить проекциями на эти координатные оси. Такое представление является разложением вектора по данному ортогональному базису.

Пусть - полный ортогональный базис, а x - некоторый вектор в данном пространстве. Зададим числаследующим образом:

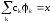и построим ряд. Равенство называется разложением вектора x по базису.

Данный ряд называют обобщенным рядом Фурье, а число - коэффициентами Фурье по данному базису.

В том случае если базис ортонормированный, т.е.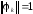. Умножив скалярно обе части равенства на вектор x, найдем

.

Равенство называетсяравенством Парсеваля.