Математические модели сообщений, сигналов и помех

1. Классификация сигналов

Определимся с понятием сигнал. Сигнал (от лат. “signum”) - физический процесс, несущий сообщение о каком-либо событии, состояния объекта, либо передающий команды управления и т.п. Т.е. сигнал - это материальный носитель сообщения. Чаще всего сигнал принято представлять в виде некоторых функций времени. Любой сигнал принято представлять в виде какой-либо модели. Простейшая модель сигнала: функция sin, cos. Зная математические модели сигналов, можно сравнивать эти сигналы между собой, устанавливать их тождество и различие, проводить классификацию. Сигналы можно классифицировать как одномерные и многомерные. Примером одномерного сигнала является напряжение на зажимах какой-либо цепи. Примером многомерного сигнала, например, система напряжений на зажимах многополюсника.

Другой принцип классификации радиотехнических сигналов основан на возможности или невозможности точного предсказания их мгновенных значений в любые моменты времени. Если математическая модель сигнала позволяет осуществить такое предсказание, то сигнал называется детерминированным. Однако, детерминированных сигналов не существует. Взаимодействие системы с окружающими ее физическими объектами, наличие хаотических тепловых флуктуаций - все это заставляет рассматривать реальные сигналы как случайные функции времени. Случайные сигналы проявляют себя как помехи, препятствующие извлечению информации из принятого колебания, но очень часто, когда уровень помех значительно меньше уровня полезного сигнала с известной формой, более простая детерминированная модель оказывается вполне адекватной.

Еще один класс сигналов представляют собой импульсы, т.е. колебания, существующие лишь в пределах конечного отрезка времени. При этом различают видеоимпульсы и радиоимпульсы.

Если 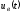- видеоимпульс, то соответствующий ему радиоимпульс

,

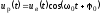где - частота,- начальная фаза. При этом функцияназываетсяогибающей радиоимпульса, а функция - егозаполнением.

Следующий класс радиотехнических сигналов - это дискретные сигналы. Простейшая модель дискретного сигнала - это счетное множество точек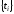на оси времени, в каждой из которых определено отсчетное значение сигнала.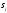

Как правило, шаг дискретизации для каждого сигнала постоянен. Одно из преимуществ дискретных сигналов по сравнению с аналоговыми - отсутствие необходимости воспроизводить сигнал непрерывно во все моменты времени. За счет этого появляется возможность по одной и той же радиолинии передавать сообщения от разных источников, организуя многоканальную связь с разделением по времени.

При решении некоторых задач в радиотехнике, например вычисление отклика физической системы на известное входное воздействие, требуются специфические формы представления сигналов. Для этого реальный сигнал приближенно представляется суммой некоторых элементарных сигналов. Наиболее распространены два способа динамического представления: в виде набора ступенчатых функций; в виде набора прямоугольных импульсов, примыкающих друг к другу.

Пусть дан сигнал, математическая модель которого задается системой равенства

Такая функция описывает процесс перехода некоторого физического объекта из “нулевого” в “единичное” состояние. Переход совершается по линейному закону за время . Если параметрустремить к нулю, то в пределе переход из одного состояния в другое будет совершаться мгновенно. Математическая модель предельного сигнала носит названиефункции включения или функции Хевисайда

.

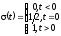С помощью функции включения можно описать любую функцию произвольного вида. При этом формула динамического представления произвольного сигнала посредством функций Хевисайда имеет вид

.

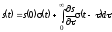Рассмотрим прямоугольный импульс, заданный в виде двух функций включения.

Площадь этого импульса при любом значении параметра (кси) равна 1. Если величинастремится к нулю, то импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предельное значение такой функции при 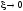(кси) стремящейся к нулю называетсядельта-функция, или функция Дирака

.

Будучи равной нулю всюду, за исключением точки , дельта функция тем не менее обладает единичным интегралом

.

Обратимся к рисунку, на котором сигнал представлен в виде совокупности прямоугольных импульсов. Если - значение сигнала на-ом отсчете, то элементарный импульс с номеромможно представить в виде

.

При динамическом представлении исходный сигнал 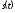должен рассматриваться как сумма таких элементарных импульсов

.

В этой сумме при любом дискретном значении отличным от нуля будет только одно слагаемое с номером, для которогои данную сумму можно представить в виде

.

При получим искомую формулу динамического представления сигнала

.

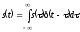Т.е. если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен -импульс. Принято говорить, что в этом состоитфильтрующее свойство дельта-функции.