Включение rlcцепи.

L

U(t)R

C

Уравнение: или

Решение:

Установившийся режим нулевой: i_уст = 0, поэтому:

Результат аналогичен полученному ранее, за исключением знака. В этом случае:

Напряжение на индуктивности:

Напряжение на активном сопротивлении:

Напряжение на ёмкости:

i , U U_C

i_L

t

i , U

U

i_L t

Пусть

Как и ранее

Для нахождения постоянных интегрирования составим два уравнения:

Из этих уравнений модно получить постоянные интегрирования A₁иA₂:

Выражение для тока в случае комплексных корней будет иметь вид:

Детальный анализ достаточно сложен. Например, если w=w`w₀, т.е.<<w₀и=/ 2. Данные соотношения справедливы для случая, когда контур с малым затуханием включается на напряжение с частотой, равной собственной частоте. Тогда:

i

t

Ток изменяется по синусоидальному закону с амплитудой, возрастающей по экспоненте. Если частоты w иw` близки друг к другу, то

В первые периоды близко к 1. Тогда

- это биения колебаний.

Операторный метод рассчета.

При решении задач классическим методом необходимо решать уравнения . Можно свести задачу к решению алгебраических уравнений

1. Если f(t) удовлетворяет условию Дирихле (на любом конченом интервале она должна быть непрерывна или иметь конечное число разрывов первого рода, а также конечное число максимумов и минимумов).

2. Если f(t)=0 при t<0

f(t)=f(t) при t>=0, то можно ввести понятие

F(p)=где p=+js

Интеграл имеет конечное значение, если f(t) растет быстрее, чем т.е.

гдеи М - конечные числа

т.е.

Обозначение: F(p)=f(t) или F(p)=L{f(t)}

Обратное преобразование Лапласа:

f(t)=

Существует преобразование по Карсону:

(p)=p [f(t)dt] = pF (p)

0

Достоинство данного преобразования - одинаковая размерность оригинала и изображения. В случае преобразования по Лапласу размерность изображения равна размерности оригинала, умноженной на размерность времени. Достоинством преобразования по Лапласу является его сходство с преобразованием Фурье, используемым для частотного анализа цепей.

Свойства преобразования по Лапласу:

1. f(t) = F(p), то Af(t) =AF(p)

2. f1(t) = F1(p) и f2(t) = F2(p), то

f1(t) + f2(t) = F1(p)+F2(p)

3. f(t) = A , то: F(p) = A/p

F(p) =[Adt] = - = [1- ]=A/p

вращающийся единичный вектор

4. f(t) = F(p), то f’(t) = pF(p) -f(0), или в общем случае:

[f’(t) dt] = f(t)-

--------- ===

U dV

- [-pf(t) dt] = -f(0) + pF(p)

при tрастет быстрее, чем f(t):

f(t)0 при t

f(t) = p [F(p) -]

Если f(0) = f’(0) = ...= f (0) , то f(t) = p F(p)

5. f(t) = F(p), то [f(t) dt ] = F(p)/p

[{[f(t) dt] }=

==== --------------

dV U

! стремится к

= - [f(t) dt]+ ! нулю при

! t

+ [f(t) dt] =

Операции интегрирования и дифференцирования заменяются в области изображений алгебраическими операциями с их изображениями.

Например

1. = L; если i(t) = I(p), то

= (p) = pLI(p) - Li(0)

2. Uc = (1/C) [ i dt] + Uc(0)

Uc(t) = Uc(p) = I (p) /pC + Uc(0)/p

6. Изображение экспоненциальной функции.

f(t) = , то F(p) = 1/(p-a)

F(p) = [dt ] =[ dt] = -=

Так как Re{p} =>a, т.е. f(t) возрастает медленнее, чем .

Если at =j(t +), то

==/[p-j]

7. f(t) = sin(t), то F(p) = /(+)

sin(t) ===/(+)

Существуют таблицы прямого и обратного преобразования Лапласа и Карсона.

Вернемся к примеру:

(R1+R3)I1 +pL1I1 -L1i1(0) + pL3I1 - L3i1(0)+

R3I2 + pL2I2 - L2i2(0) = E1

R3I1 + pL3I1 - L3i1(0) + (R2+R3)I2 + pL3I2 -

- L3i2(0) + I2/pC +Uc(0) = E2

Решая системы уравнений, получаем I1= F1(p) и I2 = F2(p).

После чего переходим к оригиналу. Необходимо отметить, что при составлении уравнения в операторной форме учитываются начальные условия.

ЗАКОНЫ КИРХГОФА И ОМА В ОПЕРАТОРНОЙ ФОРМЕ.

Для узла: [i(t) ] = 0 [I(p)] =0

Для контура: [U(t)] =[e(t)]

[U(p)] =[e(p)]

Необходимо точно выдерживать правило знаков, т.е. задаваться положительными направлениями токов.

Рассмотрим в качестве примера RLC цепь:

Uk(t) = R(i) + Uc(0) + [i(t) dt] + L

Применяя преобразование Лапласа получим:

Uk(p) = RI(p) + pLI(p) - Li(0) + I(p)/(pC) + !Uc

-----------------U1(p) + Uc(0)/p !

Uk(p) + Li(0) - Uc(0)/p = [R+ pL + 1/(pC)]I(p)

Операторная форма записи закона Ома, используемая для расчета переходных процессов:

Z(p) - операторное ( обобщенное) сопротивление.

При нулевых начальных условиях I(p) = Uk(p)/Z(p).

При нулевых начальных условиях расчет переходных про цессов операторным методом совпадает с расчетом установившихся прцессов комплексным методом, кроме отыскания оригинала.

При ненулевых начальных условиях при переходе в область изображений каждый элемент заменяется в соответствии:

Элементы, запасающие энергию, превращаются в активные.

При последовательном соединении двухполюсников:

E (p) + L i (0) - Uc (0) /p = I(p) Z (p)

При нулевых E(p) = I(p)Z(p)

начальных условиях

При последовательном соединении операторные сопротивления складываются.

Если рассматривать два пассивных двухполюсника, включенных параллельно:

U(p) = I1(p)Z1(p) - L1i1(0) + Uc1(0)/p

U(p) = I2(p)Z2(p) - L2i1(0) + Uc2(0)/p

I(p) = [U(p) +L1i1(0) - Uc1(0)/p]/Z1(p) + [U(p) + L2i2(0) - Uc2(0)/p]/Z2(p)

При ненулевых начальных условиях ток нельзя представить в виде произведения U(p) на Y(p), имеющей смысл операторной прводимости.

Только при нулевых начальных условиях можно записать:

I(p) = U(p)[1/Z1(p) + 1/Z2(p) ] = U(p)[Y1(p) + Y2(p)]

Можно ввести понятие операторной проводимости:

Y(p) = 1/Z(p)

РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ.

1. Включение RL на постоянное напряжение.

E(t) = const ; E(p) = E/p

I(p)=]

2. Включение RC на постоянное напряжение.

=

3. Включение RLС цепи на постоянное напряжение при нулевых начальных условиях.

а) можно записать диф. уравнение, затем преобразовать по Лапласу;

б) можно записать из закона Ома в операторной форме.

Введем обозначения:

R/2L = ; 1/=;=

можно по

Получим: таблицам

Оригинал: i(t) = sin(t)

Если имеем функцию не от p, а от (p+ ) - сдвиг функции, то оригинал умножается на.

ПЕРЕХОД ОТ ИЗОБРАЖЕНИЯ К ОРИГИНАЛУ.

f(t) = [F(p)dp] - можно и так.

Существуют таблицы. Для расширения возможности пользования таблицами рассмотрим несколько функций.

1. Единичная функция Хевисайда (для записи момента коммутации)

0 при t<0

i(t) =

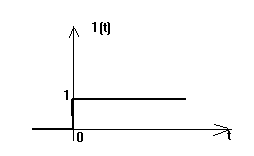
1 при t>=0

Включение постоянного напряжения в момент времени t=0 записывается как U1(t), напряжения произвольной формы - U(t)1(t).

Если коммутация происходит при t1>0, то U(t)1(t-t1).

2. ТЕОРЕМА ЗАПАЗДЫВАНИЯ (СМЕЩЕНИЯ).

Дано f(t) =F(p)

Найти изображение 1(t-t1)f(t-t1),

т.е. функции, совпадающей с исходной

по форме, но сдвинутой по времени на t1.

Введем обозначения:

[f(t - t1)dt] == t - t1; dt = d

t = t1 +

= [f()d] =[f() d] = F(p)

Изображение исходной функции, смещенной во времени на t1, равно изображению исходной функции, умноженной на .

Обратная задача. Дано: f(t) = F(p). Требуется найти f1(t) = F(p+a), т.е. смещение изображения на а в общем случае комплексное.

f1(t) = f(t) = F(p+a)

Пример. На RL цепочку подается импульс. Требуется определить ток i(t).

Импульс можно представить как

U1(t) - U1(t-t1), т.е. сумма напряжений

разного знака и одинаковой величины,

сддвинутых на время tи.

Изображение такого напряжения:

=U . 222

Для первого слагаемого Для второго слагаемого

0 t<0 0 t<tи

t>0 t>tи

[1 -] [1- ]

Следовательно: i(t) = i1(t) - i2(t)

t<0: 0

0<t<tи : [1 -]

t<tи:{[1 -]1(t) - [1 -]1(t-tи)}

ТЕОРЕМА РАЗЛОЖЕНИЯ.

Пусть имеем изображение, заданное дробно - рациональной функцией, причем степень полинома числителя меньше степени полинома знаменателя:

F(p) = G(p)/H(p), где G(p) и H(p) - полиномы с действительными коэффициентами.

Допустим, что уравнение H(p)=0 не имеет кратных корней и корней, равных корням G(p) = 0. При этих условиях F(p) можно разложить на простые дроби:

n - степень полинома знаменателя H(p), p(i) - корни уравнения H(p) = 0.

Умножим обе части уравнения на (p - pk)

ppk

По правилу Лапиталя неопределенность раскрывается как отношение производной числителя к производной знаменателя.

Значит и F(p) =

Поскольку Ak/(p-pk) = Ak, то

f(t) =

Частный случай 1. р1 = 0 . В схеме ддействует постоянная ЭДС или ток и первый член представляет собой установившееся значение.

F(p) = f(t) = +

G(0)/H’(p) - установившийся ток или напряжение.

Частный случай 2. H(p) =0 имеет пару чисто мнимых корней p1 = j;

p2 = -j.

Комплексные корни обязательно должны образовывать комплексно - сопряженные пары, поскольку коэффициенты характеристического уравнения - действительные числа.

F(p) = f(t) = + +

Первые два члена разложения представляют установившееся значение на переменном токе (если есть источники синусоидальных сигналов).

Частный случай 3. Корень уравнения H(p) = 0 имеет кратность q. В этом случае дробно - рациональную функцию можно разложить:

(p - p1) H1(p) (p-p1) (p-p1)

Оригинал имеет вид:

Полезно помнить важные свойства функций f(t) при t0 и t:

f(0+) = lim pF(p); f() = lim pF(p)

pp0

ПОРЯДОК РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ.

Могут быть использованы все методы расчета на постоянном токе. Существуют два пути:

I.

1. Составляем диф. уравнения.

2. Применяем пряямое преобразование Лапласа и находим решение в области изображений в виде: F(p) = G(p)/H(p).

3. Полином знаменателя разлагается на два сомножителя:

H(p) = N(p)H1(p), где :

N(p) = 0 - корни определяют установившийсяя прцесс;

H1(p) = 0 - совпадает с характеристическим уравнением, составленным для решения задачи ил. методом. Оно определяет свободную

составляющую переходного процесса.

4. Находим оригинал полученного изображения.

II.

1. Заменяем исходную электрическую схему операторной схемой замещения ( с учетом ненулевых начальных условий для элементов, способных накапливать энергию).

2. Для операторной схемы замещения составляют уравнения по законам Кирхгофа или с использованием всех известных методов. По сути дела это соответствует расчету цепей на постоянном токе.

3. Находим изображение искомой функции:

F(p) = G(p)/H(p).

4. Далее последовательность определения f(t) аналогична изложенной ранее.