Решение задачи с помощью явной разностной схемы

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. Явная конечно-разностная схема для данной задачи получается, если использовать шаблон I рассмотренный в “Теоретические сведения”.

2.1 Аппроксимация дифференциального уравнения

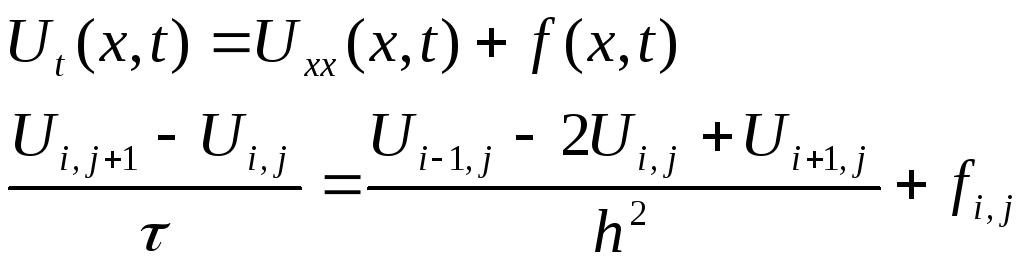
Значение температуры на j+1 слое явно вырежется через значение температуры на j слое по формуле:

2.2 Аппроксимация начального условия.

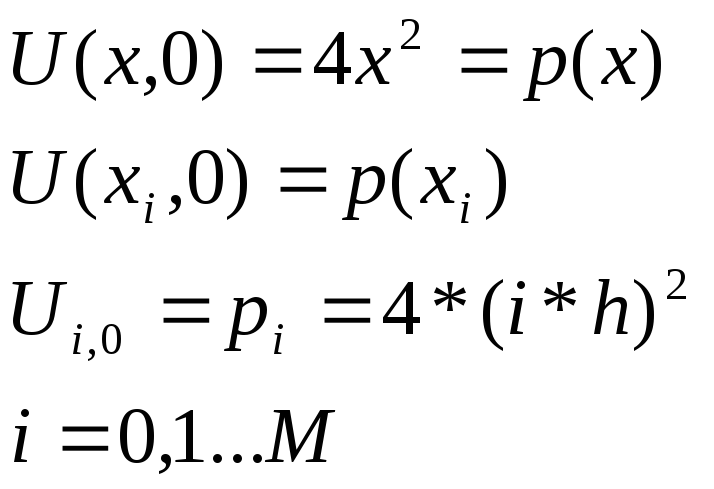
2.3 Аппроксимация 1-го граничного условия.

Для аппроксимации граничного условия второго рода разложим в ряд Тейлора функцию в окрестности точки (0,t):

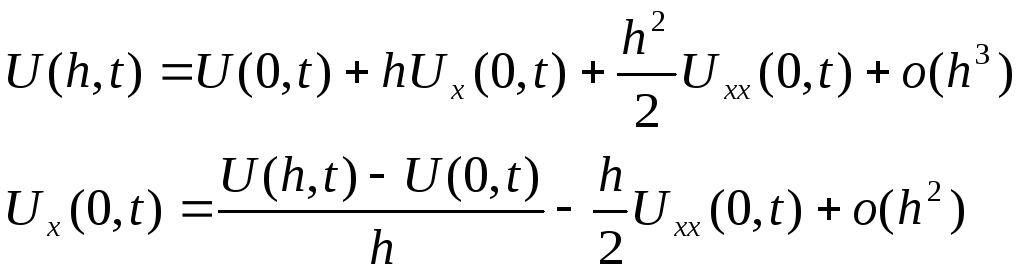
Подставим сюда из уравнения теплопроводности и выразим производнуюв точке:

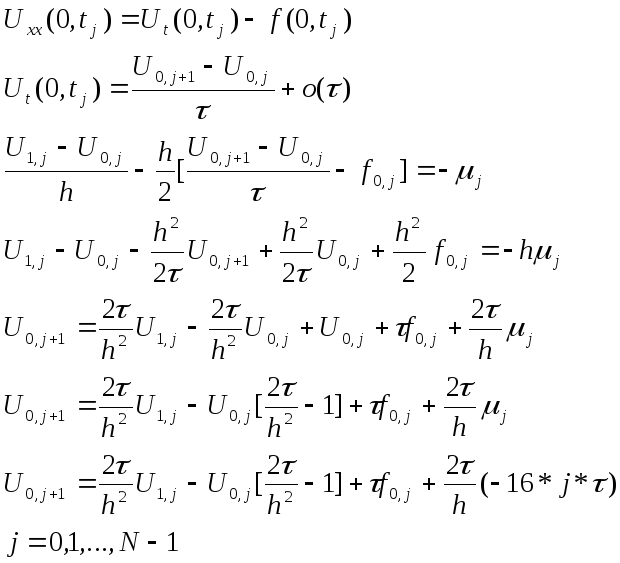
2.4 Аппроксимация 2-го граничного условия.

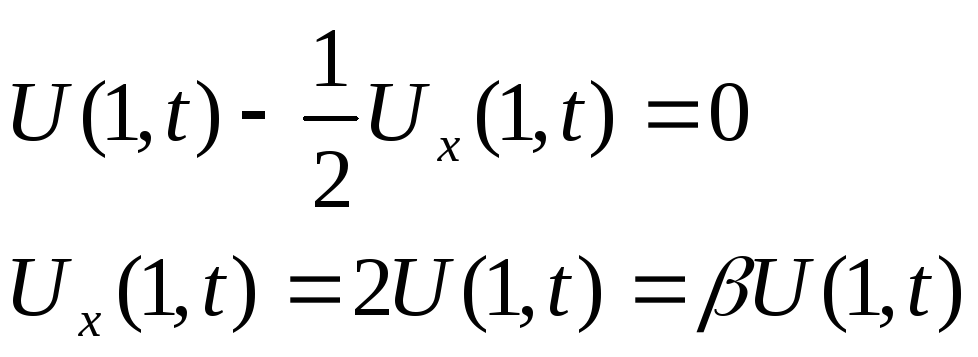
Для аппроксимации граничного условия третьего рода разложим в ряд Тейлора функцию в окрестности точки (1,t):

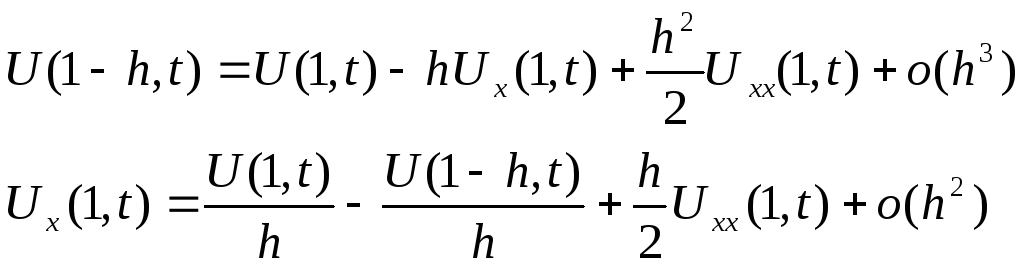
Подставим сюда из уравнения теплопроводности и выразим производнуюв точке:

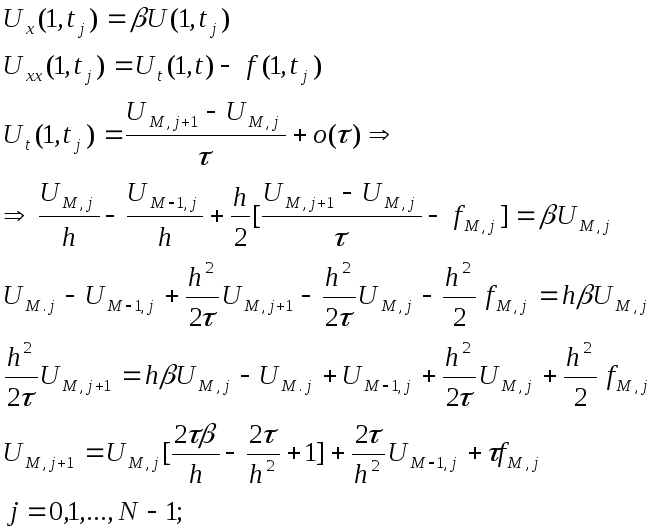
Порядок аппроксимации данной разностной схемы

Практическая реализация данного метода возможна лишь при таких соотношениях между шагами сетки ипри которых выполняется условие устойчивости решения к ошибкам округления и неточностям в начальных данных. Это условие имеет вид. Текст функции, вычисляющий матрицу решения размерностьюприведён в приложении.

Решение задачи с помощью неявной разностной схемы

Рассмотрим снова нашу краевую задачу. Для аппроксимации уравнения используем шаблон IIописанный в “Теоретические сведенья”. Уравнение аппроксимируется следующими уравнениями:

3.1 Аппроксимация дифференциального уравнения

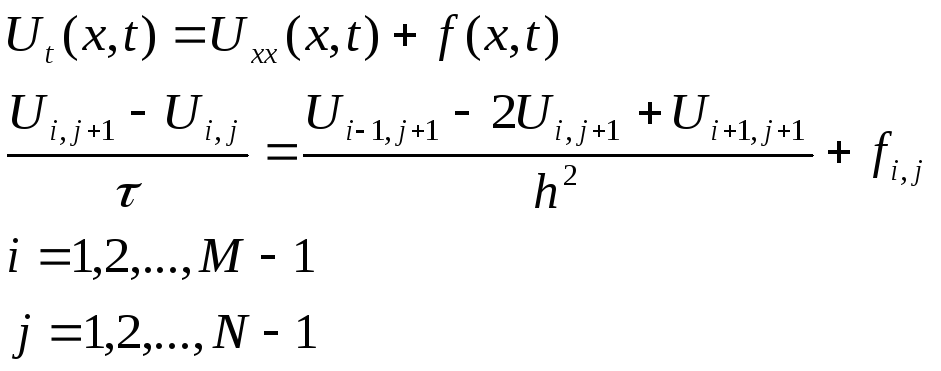
Перепишем полученное выражение в виде удобном для применения метода прогонки:

3.2 Аппроксимация начального условия

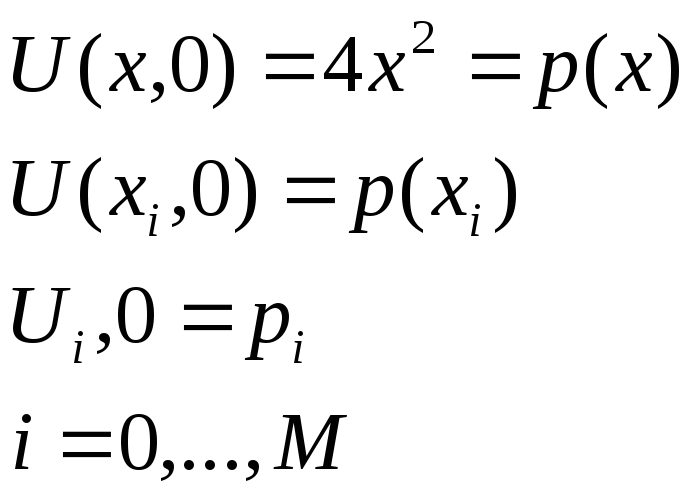
3.3 Аппроксимация 1-ого граничного условия

Для аппроксимации граничного условия второго рода разложим в ряд Тейлора функцию в окрестности точки (0,t):

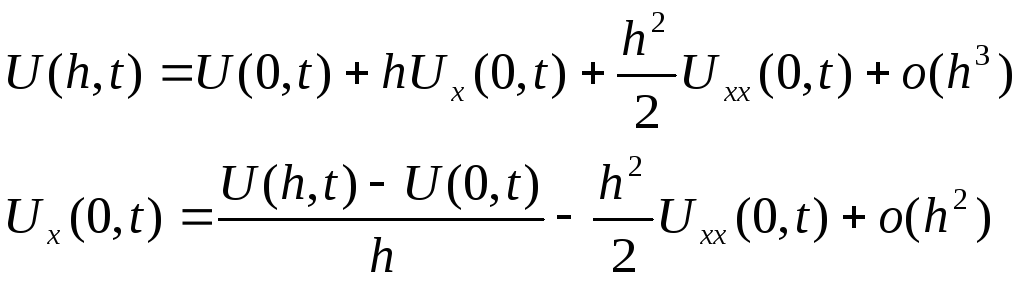
Подставим в полученное выражение из уравнения теплопроводности и выразим при

Производную заменим левой разностной производной:

3.4 Аппроксимация 2-го граничного условия

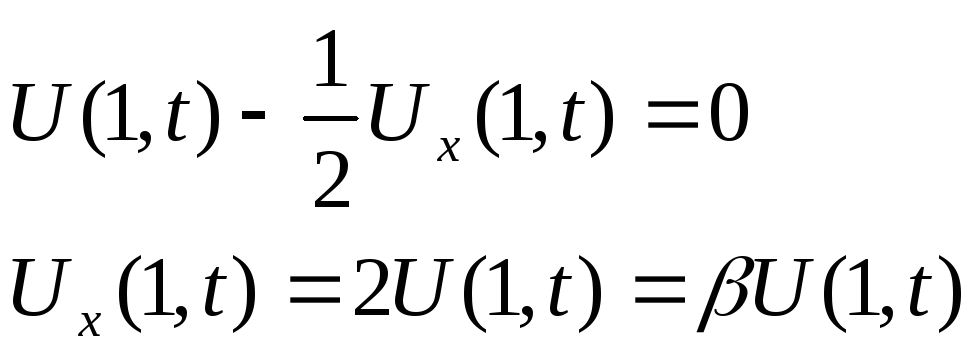
Для аппроксимации граничного условия третьего рода разложим в ряд Тейлора функцию в окрестности точки (1,t):

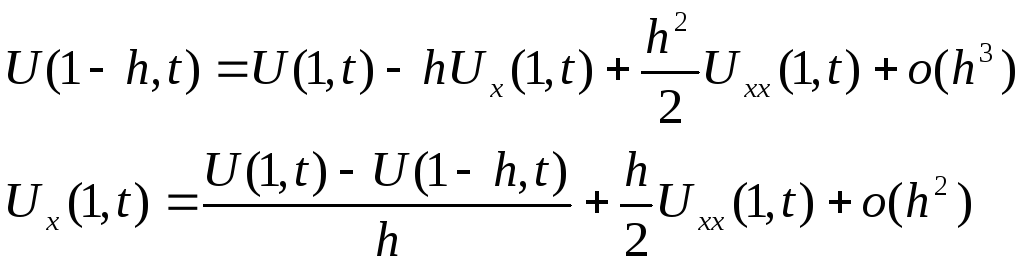
Подставим в полученное выражение из уравнения теплопроводности и выразим при

Производную заменим левой разностной производной:

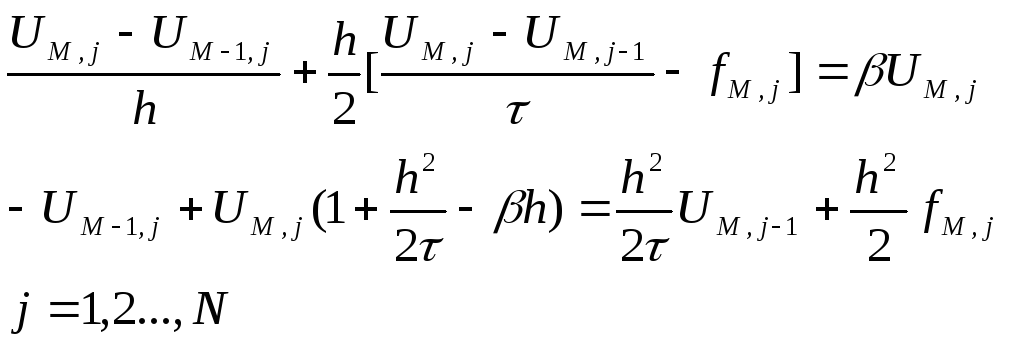
Порядок аппроксимации данной разностной схемы

3.5 Метод прогонки:

Перепишем получившееся равенства в систему, удобную для применения метода прогонки:

(*)

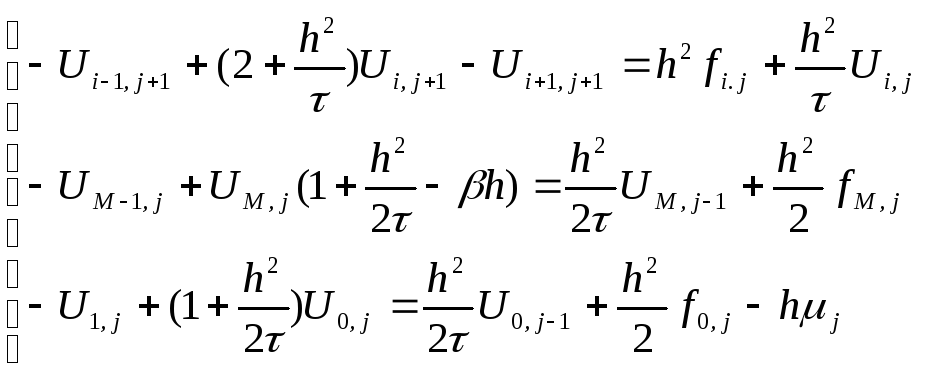Прогоночные коэффициенты:

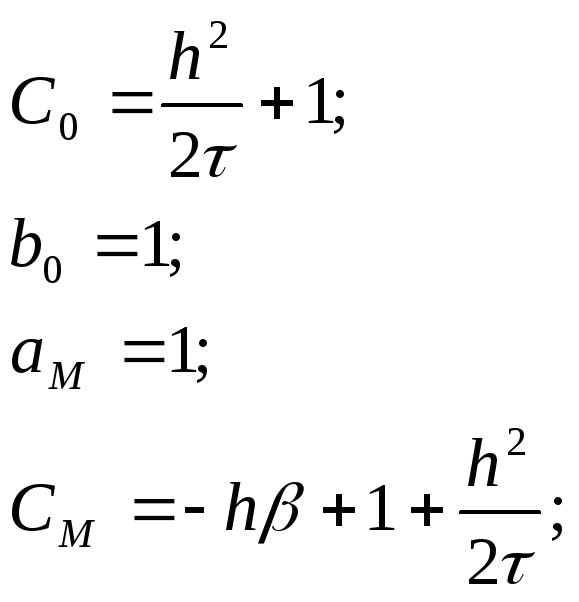
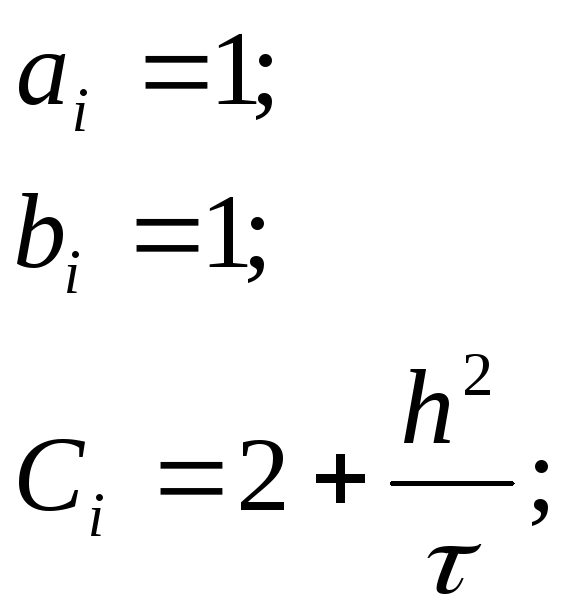
<<Теорема: Пусть коэффициенты системы (*) удовлетворяют следующим условиям:

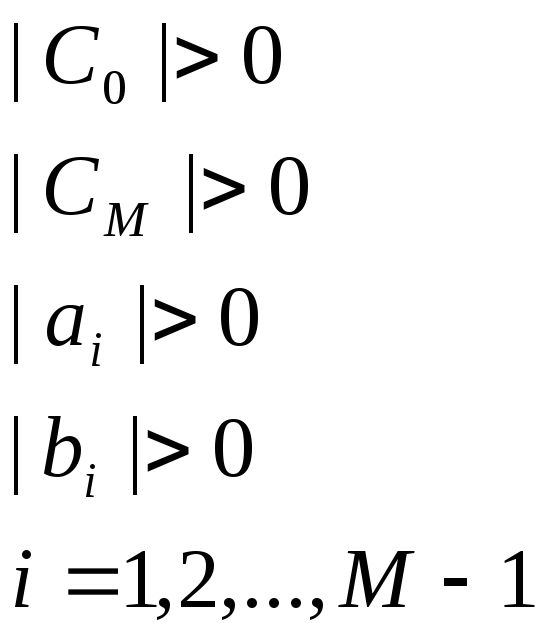
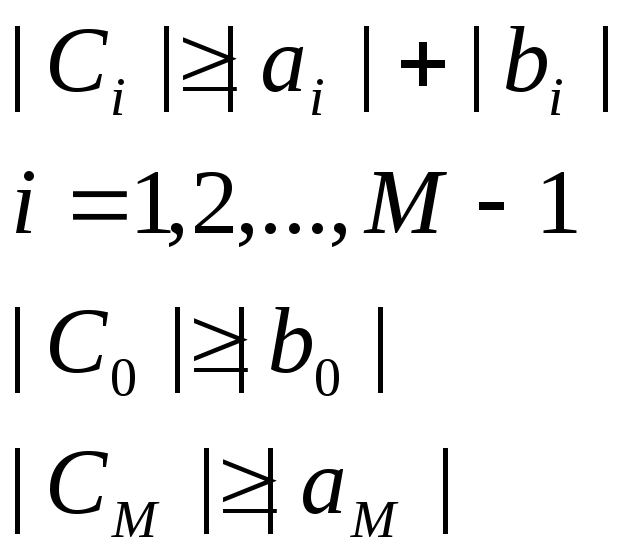
Причем хотя бы одно из данных неравенств является строгим. Тогда для метода прогонки реализующего неявную разностную схему, имеют место неравенства

гарантирующие корректность и устойчивость метода прогонки.>>

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ:

Таблицы результатов:

При M = 100, N = 20000, т.е. при h = 1/100, t = 1/20000 получены следующие результаты:

X = 0;0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1;

T = 0;0.1;0.2;0.3;0.4;0.5;0.6;0.7;0.8;0.9;1;

1. Явная разностная схема:

U(x,t)

0 0.3922 0.4308 0.3191 0.1833 0.1233 0.2409 0.6642 1.5742 3.2396 6.0679

0.0400 0.5637 0.7513 0.7962 0.8224 0.9292 1.2191 1.8223 2.9230 4.7957 7.8563

0.1600 0.7696 1.0874 1.2848 1.4794 1.7692 2.2590 3.0847 4.4413 6.6199 10.0625

0.3600 1.0246 1.4597 1.8105 2.1848 2.6785 3.4007 4.4976 6.1823 8.7748 12.7619

0.6400 1.3413 1.8884 2.3997 2.9706 3.6949 4.6885 6.1132 8.2084 11.3365 16.0496

1.0000 1.7310 2.3940 3.0802 3.8708 4.8592 6.1712 7.9901 10.5917 14.3956 20.0431

1.4400 2.2047 2.9979 3.8813 4.9226 6.2165 7.9033 10.1953 13.4158 18.0599 24.8852

1.9600 2.7746 3.7233 4.8352 6.1664 7.8165 9.9460 12.8048 16.7781 22.4571 30.7481

2.5600 3.4548 4.5962 5.9776 7.6472 9.7147 12.3681 15.9060 20.7918 27.7383 37.8396

3.2400 4.2633 5.6465 7.3485 9.4154 11.9738 15.2483 19.5995 25.5893 34.0829 46.4088

4.0000 5.2231 6.9090 8.9934 11.5279 14.6646 18.6762 24.0018 31.3260 41.7040 56.7558

1.2Неявная разностная схема:

U(x,t)

0 0.3922 0.4308 0.3191 0.1834 0.1235 0.2412 0.6647 1.5749 3.2409 6.0699

0.0400 0.5637 0.7513 0.7963 0.8225 0.9293 1.2194 1.8228 2.9238 4.7970 7.8583

0.1600 0.7696 1.0874 1.2848 1.4795 1.7694 2.2593 3.0852 4.4421 6.6212 10.0646

0.3600 1.0246 1.4597 1.8105 2.1849 2.6787 3.4010 4.4982 6.1833 8.7763 12.7642

0.6400 1.3413 1.8884 2.3998 2.9707 3.6951 4.6888 6.1138 8.2095 11.3382 16.0523

1.0000 1.7310 2.3941 3.0802 3.8709 4.8595 6.1716 7.9909 10.5929 14.3976 20.0463

1.4400 2.2047 2.9979 3.8814 4.9227 6.2168 7.9039 10.1962 13.4173 18.0623 24.8889

1.9600 2.7746 3.7233 4.8353 6.1665 7.8168 9.9466 12.8059 16.7799 22.4599 30.7526

2.5600 3.4548 4.5962 5.9777 7.6474 9.7152 12.3689 15.9073 20.7939 27.7417 37.8450

3.2400 4.2633 5.6465 7.3486 9.4157 11.9743 15.2492 19.6011 25.5918 34.0870 46.4154

4.0000 5.2231 6.9091 8.9935 11.5282 14.6653 18.6774 24.0037 31.3292 41.7091 56.7638

1.4 Значение Нормы

0.00800219828546

График поверхности

1.1Явная схема

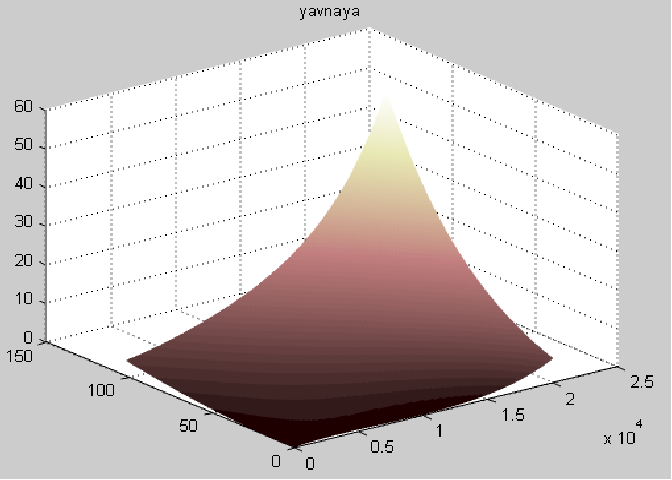
2. Неявная разностная схема

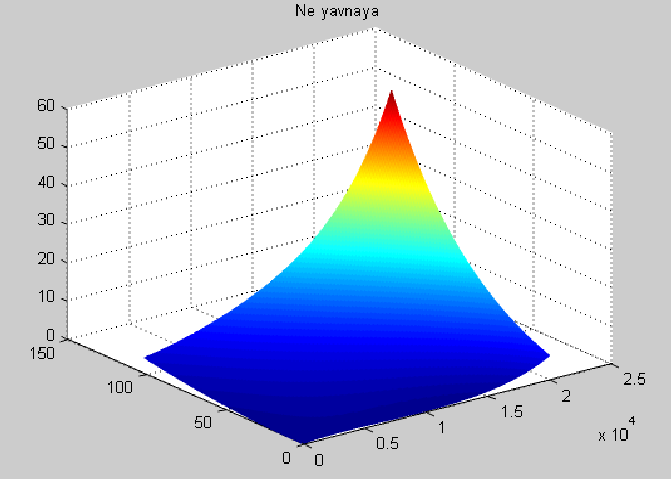
Графики слоев t = 0 : 0.2 : 1.

1.1 Не явная схема:

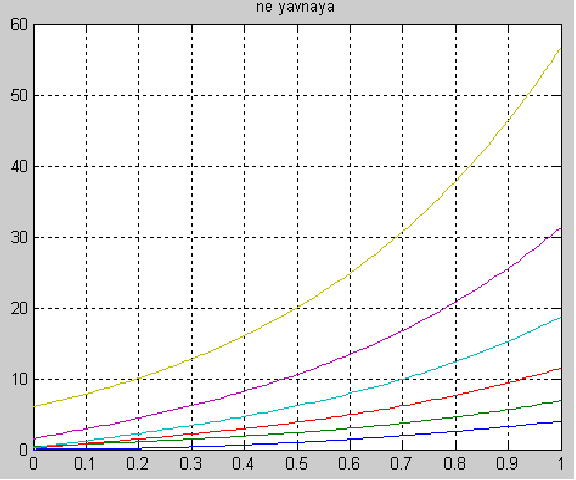
1.2Явная схема