Общепринятые октавные полосы частот

Октавные полосы частот	min, Гц	max, Гц	ср, Гц
1	45	90	63
2	90	180	125
3	180	355	250
4	355	710	500
5	710	1400	1000
6	1400	2800	2000
7	2800	5600	4000
8	5600	12000	8000

Примеры интервалов частот звука, создаваемого человеческим голосовым аппаратом и воспринимаемого человеческим слуховым аппаратом, приведены в табл.4.

Табл. 4

Частота женского голоса, Гц		Частота мужского голоса, Гц
Контральто, альт	170 – 780	Бас	80 – 350
Меццо-сопрано	200 – 900	Баритон	100 – 400
Сопрано	250 – 1000	Тенор	130 – 500
Колоратурное сопрано	260 – 1400

Примеры частотных диапазонов некоторых музыкальных инструментов приведены в таблице 5. Они охватывают не только звуковой диапазон, но и ультразвуковой.

Табл. 5

Музыкальный инструмент	Частота, Гц
Орган	22 – 16 000
Саксофон	80 – 8 000
Рояль	90 – 9 000
Барабан	90 – 14 000
Скрипка	260 – 15 000

Животные, птицы и насекомые создают и воспринимают звук других частотных диапазонов, нежели человек (табл. 6).

Табл. 6

Живые существа	Частота, Гц
Собака	200 – 60 000
Кошка	250 – 120 000
Рыба	300 – 8 000
Медведь	300 – 80 000
Дельфин	400 – 200 000
Бабочка	8000 – 160 000

В музыке каждую синусоидальную звуковую волну называют простым тоном, или тоном. Высота тона зависит от частоты: чем больше частота, тем выше тон. Основным тоном сложного музыкального звука называют тон, соответствующий наименьшей частоте в его спектре. Тоны, соответствующие остальным частотам, называются обертонами. Если обертоны кратны частоте основного тона, то обертоны называются гармоническими. Обертон с наименьшей частотой называется первой гармоникой, со следующей — второй и т.л.

Музыкальные звуки с одним и тем же основным тоном могут различаться тембром. Тембр зависит от состава обертонов, их частот и амплитуд, характера их нарастания в начале звучания и спада в конце.

Скорость звука

Для звука в различных средах справедливы общие формулы (22) – (25). При этом следует учесть, что формула (22) применима в случае сухого атмосферного воздуха и с учётом числовых значений коэффициента Пуассона, молярной массы и универсальной газовой постоянной может быть записана в виде:

.

Однако, реальный атмосферный воздух всегда имеет влажность, которая влияет на скорость звука. Это обусловлено тем, что коэффициент Пуассона  зависит от отношения парциального давления водяного пара (p_пар) к атмосферному давлению (p). Во влажном воздухе скорость звука определяют по формуле:

.

Из последнего уравнения видно, что скорость звука о влажном воздухе скорость звука немного больше, чем в сухом.

Численные оценки скорости звука, учитывающие влияние температур и влажности атмосферного воздуха, можно осуществлять по приближённой формуле:

. (22*)

Эти оценки показывают, что при распространении звука вдоль горизонтального направления (0x) с увеличением температуры на 1 ⁰C скорость звука возрастает на 0,6 м/с. Под влиянием водяного пара с парциальным давлением не более 10 Па скорость звука возрастает менее чем на 0,5 м/с. А в целом, при максимально возможном парциальном давлении водяного пара у поверхности Земли, скорость звука увеличивается не более чем 1 м/с.

Звуковое давление

При отсутствии звука атмосфера (воздух) является невозмущённой средой и имеет статическое атмосферное давление ( ).

При распространении звуковых волн к этому статическому давлению добавляется дополнительное переменное давление, обусловленное сгущениями и разрежениями воздуха. В случае плоских волн можно записать:

, (42)

где p_зв,max – амплитуда звукового давления,  - циклическая частота звука, k – волновое число. Следовательно, атмосферное давление в фиксированной точке в данный момент времени становится равным сумме этих давлений:

.

Звуковое давление – это переменное давление, равное разности мгновенного фактического атмосферного давления в данной точке при прохождении звуковой волны и статического атмосферного давления при отсутствии звука:

. (43)

Звуковое давление в течение периода колебаний меняет своё значение и знак.

Звуковое давление практически всегда намного меньше атмосферного

.

Оно становится велико и соизмеримо с атмосферным при возникновении ударных волн во время мощных взрывов или при прохождении реактивного самолета.

Единицами измерения звукового давления служат следующие:

- паскаль в СИ ,

- бар в СГС ,

- миллиметр ртутного столба ,

- атмосфера .

На практике приборы измеряют не мгновенное значение звукового давления, а так называемое эффективное (или действующее) звуковое давление. Оно равно квадратному корню из среднего значения квадрата мгновенного звукового давления в данной точке пространства в данный момент времени

(44)

и поэтому называется также среднеквадратическим звуковым давлением. Подставляя выражение (39) в формулу (40), получим:

или

. (45)

Звуковое сопротивление

Звуковым (акустическим) сопротивлением называют отношение амплитуд звукового давления и колебательной скорости частиц среды:

. (46)

Физический смысл звукового сопротивления: оно численно равно звуковому давлению, вызывающему колебания частиц среды с единичной скоростью:

.

Единица измерения звукового сопротивления в СИ – паскаль-секунда на метр:

.

В случае плоской волны скорость колебаний частиц равна

,

.

Тогда формула (46) примет вид:

. (46*)

Существует также и другое определение звукового сопротивления, как произведение плотности среды и скорости звука в этой среде:

. (47)

Тогда его физический смысл состоит в том, что оно численно равно плотности среды, в которой распространяется упругая волна с единичной скоростью:

.

Кроме акустического сопротивления в акустике используется понятие механическое сопротивление (R_м). Механическое сопротивление представляет собой отношение амплитуд периодической силы и колебательной скорости частиц среды:

, (48)

где S – площадь поверхности излучателя звука. Механическое сопротивление измеряется в ньютон-секундах на метр:

.

Энергия и сила звука

Звуковая волна характеризуется теми же энергетическими величинами, что и упругая волна.

Каждый объем воздуха, в котором распространяются звуковые волны, обладает энергией, складывающейся из кинетической энергии колеблющихся частиц и потенциальной энергии упругой деформации среды (см. формулу (29)).

Интенсивность звука принято называть силой звука. Она равна

. (49)

Поэтому физический смысл силы звука аналогичен смыслу плотности потока энергии: численно равна среднему значению энергии, которая переносится волной за единицу времени через поперечную поверхность единичной площади.

.

Единица измерения силы звука – ватт на квадратный метр:

.

Сила звука пропорциональна квадрату эффективного звукового давления и обратно пропорциональна звуковому (акустическому) давлению:

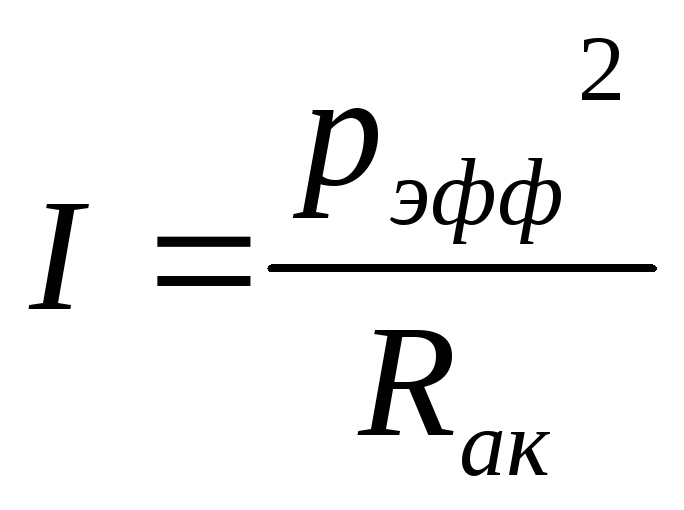, (50)

или, учитывая выражения (45),

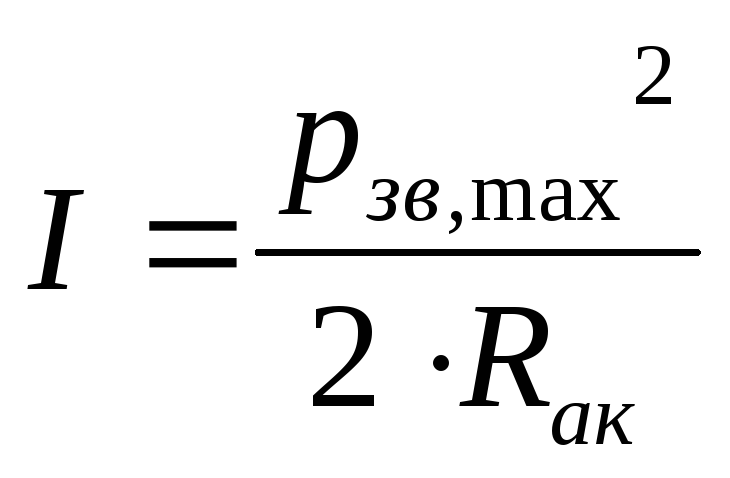, (51)

где R_ак – акустическое сопротивление.

Звук можно также характеризовать звуковой мощностью. Звуковая мощность – это общее количество звуковой энергии, излучаемой источником в течение определённого времени через замкнутую поверхность, окружающую источник звука:

, (52)

или, учитывая формулу (49),

. (52*)

Звуковая мощность, как и любая другая, измеряется в ваттах:

.