Обработка изображений / Лекции по обработке изображений Ч 2

видов размытий фильтр может просто не существовать, например, при линейном сдвиге, когда H m, n 0 для некоторых заданных частот. Кроме того, инверсный фильтр обычно усиливает высокие шумовые частоты. Поскольку Hinv H 1 – должно выполняться, а обычно на низких частотах H имеет большое значение, а на высоких малое, тогда как Hinv наоборот.

Практически инверсная фильтрация только «ухудшает» изображение. Существуют частные методы ослабления шумов, которые заключаются в

ограничении полосы инверсного фильтра. Последовательно с инверсным фильтром включается корректирующее звено, модуль передаточной функции которого стремится к нулю за пределами некоторой наперед заданной граничной частоты. При этом граничная частота выбирается из компромисса между снижением уровня шума и четкостью восстановленного изображения. Однако эти методы не решают проблем краевых эффектов и наличия нулей передаточной функции формирующей системы в рабочем диапазоне частот.

Таким образом, несмотря на очевидную простоту метода инверсной фильтрации, он может успешно использоваться для восстановления ограниченного класса изображений, у которых уровень фона на краях постоянен. Кроме того, метод инверсной фильтрации обладает чрезвычайно низкой помехоустойчивостью.

Решение Винера. Частотная характеристика такого фильтра HW m, n

выбирается таким образом, чтобы минимизировать среднеквадратичную ошибку восстановления E2 , определяемую выражением

винеровский фильтр является аппроксимацией псевдоинверсного фильтра, определяемого выражением

Анализируя соотношения (3.28) и (3.29), можно отметить следующее:

1. При отсутствии шума фильтр Винера переходит в инверсный фильтр. Следовательно, в области низких частот, где, как правило, отношение сигнал/шум велико, передаточные функции инверсного и винеровского фильтров практически совпадают. Инверсный фильтр является сингулярным, т.к. модуль его передаточной функции становится бесконечно большим на пространственных частотах, соответствующих нулевым значениям модуля

51

передаточной функции искажающей системы. Причем наличие даже относительно слабого шума приводит к появлению интенсивных шумовых составляющих на выходе инверсного фильтра, полностью разрушающих изображение.

2.При уменьшении спектральной плотности мощности исходного изображения передаточная функция фильтра Винера стремится к нулю. Для изображений это характерно на верхних частотах.

3.На частотах, соответствующих нулям передаточной функции формирующей системы, передаточная функция фильтра Винера также равна нулю. В этом случае решается проблема сингулярности восстанавливающего фильтра.

Таким образом, за счет использования информации о спектральных характеристиках изображения и шума, фильтр Винера обладает относительно высокой помехоустойчивостью и у него отсутствует сингулярность, обусловленная нулями передаточной функции формирующей системы. Основным недостатком фильтра Винера остается наличие краевых эффектов, которые проявляются в виде осциллирующей помехи, маскирующей восстановленное изображение. Эта помеха появляется вследствие того, что искаженное изображение записывается в кадре конечного размера, а в усеченном изображении происходит потеря информации, содержащейся в исходном изображении вблизи границ. Поэтому при коррекции линейных искажений усеченного изображения возникают ложные детали в виде ряби или полос, интенсивность которых особенно велика при цилиндрической форме функции рассеяния точки и равномерном смазе.

Устранение смаза и размытия изображений может осуществляться программно и с помощью когерентного оптического процессора. В программе пользователь обычно задает функцию рассеяния точки (радиус кружка нерезкости) при устранении размытия и длину смаза и его направление при устранении смаза. Кроме того, пользователю предоставляются программные средства для определения типа размытия – вычисления спектров Фурье, кепстров размытых изображений. Затем рассчитывается инверсный регуляризированный фильтр вида:

восстановления оценивается пользователем. Пользователь может изменять как параметры функции размытия или смаза, так и выбирать значения стабилизи рующего множителя .

На рис. 3.11 приведено исходное размытое электронно-микроскопическое изображение пленки состава Co-Gd (а), ее спектр Фурье (б), восстановленное изображение (в) и его спектр – (г).

52

Рис. 3.11. Устранение размытия на изображении аморфной пленки:

а) – исходное размытое изображение, б) – спектр этого изображения, в) – восстановленное изображение и г) – его спектр

Восстановление изображения осуществлялось на ЭВМ путем подбора радиуса кружка рассеяния импульсной характеристики размытия и стабилизирующего множителя .

53

3.6. Согласованная фильтрация изображений

Применяемый для обработки изображений согласованный фильтр представляет собой пространственный фильтр, выходной сигнал которого есть мера пространственной корреляции между входным и эталонным изображениями. Этот сигнал затем можно использовать, например, для обнаружения заданного изображения или для пространственной привязки двух изображений. В электронной микроскопии эта задача очень актуальна, поскольку при получении изображений очень трудно следить за одним и тем же участком образца, например, при его нагреве или наблюдениях в высоковольтном микроскопе. Кроме того, согласованная фильтрация позволяет установить меру изменений в объекте при различных на него воздействиях.

Если неизвестное изображение состоит из сигнала-изображения, смещенного на расстояние x , y и аддитивного шума:

Пик корреляции будет иметь место при x x , y y в выходной плоскости;

отсюда находится величина смещения входного изображения относительно эталонного. Следовательно, согласованный фильтр инвариантен относительно сдвига. Однако он не инвариантен относительно поворота изображения, которое требуется обнаружить.

Хорнер и Джанино (1984 г., США) предложили схему чисто фазового согласованного фильтра (ЧФФ), когда используется только фазовая часть фильтра, а амплитудная часть имеет постоянные значения равные единице. ЧФФ открывает гораздо более широкие возможности для распознавания на фоне шума. Значительно более высокий корреляционный максимум у ЧФФ объясняется просто – сохранением энергии. Во-первых, в случае ЧФФ нет потерь энергии в плоскости фильтра, поскольку отсутствует амплитудная модуляция, ослабляющая энергию, а, во-вторых, эта энергия, поступающая в корреляционную плоскость, концентрируется в значительно более узком максимуме, который в большинстве случаев аппроксимируется дельтафункцией. Другое достоинство ЧФФ состоит в уменьшении объема данных, необходимых для записи фильтра, поскольку в случае ЧФФ остается только фазовая информация. Еще меньшую память требует двоичный чисто фазовый фильтр (ДЧФФ).

Для выполнения согласованной фильтрации обычно используется

втором этапе пользователю предлагается сформировать тот или иной тип фильтра:

1.H m, n A m, n exp i m, n – обычный согласованный фильтр;

2.H m, n exp i m, n – чисто фазовый фильтр;

54

двоичный чисто фазовый фильтр.

На третьем этапе вычисляется свертка вновь предъявленного изображения с выбранным пользователем фильтром. На рис. 3.12 приведены результаты согласованной фильтрации модельного изображения с квазипериодической спектральной плотностью с использованием различных фильтров.

Рис. 3.12. Согласованная фильтрация изображения:

а) – исходное изображение; б), в), г) – корреляционные функции, полученные с использованием обычного, чисто фазового и двоичного чисто-фазового согласованных фильтров соответственно

55

4. Моделирование и анализ изображений на основе ортогональных преобразований

4.1. Ортогональные преобразования

Спектральный анализ и фильтрация изображений на основе преобразования Фурье широко применяются в электронной и оптической

квазидетерминированных изображений и оценивание спектральных плотностей и корреляционных функций двумерных случайных полей) – важнейшее направление в обработке микроскопических изображений. Актуальность использования спектрального анализа при исследовании микроструктуры различных сред и материалов обусловлена, прежде всего, тем, что в частотной области наиболее просто локализовать и количественно описать упорядочения в структуре, параметризировать понятие ее анизотропии, использовать методики анализа микроструктуры по электронно-оптическим дифракционным картинам.

Пространственно-частотная фильтрация позволяет на микроскопических изображениях компенсировать аберрации оптических систем микроскопов, устранять шумы, смаз и размытие изображений, осуществлять поиск нужного фрагмента на зашумленных изображениях, подчеркивать границы неоднородностей и слабо выраженные регулярные компоненты, удалять низкочастотные тренды освещенности.

Однако для анализа и фильтрации, как правило, больших по информационной емкости (до нескольких Гбайт) микроскопических изображений вместо дискретного преобразования Фурье во многих случаях предпочтительнее использовать другие ортогональные преобразования. Например, для косинусного преобразования разработаны алгоритмы, позволяющие осуществлять данное преобразование значительно быстрее, чем вычисляется преобразование Фурье, при существенно меньшем требуемом для вычислений объеме памяти и практическом отсутствии краевых эффектов в процедуре циклической фильтрации.

В данном разделе рассматриваются методы и алгоритмы моделирования, спектрального анализа и фильтрации микроскопических изображений на основе различных ортогональных преобразований, в том числе и вейвлетпреобразований, которые более эффективны, чем методы и алгоритмы,

преобразуется в матрицу FT u1 ,u2 того же размера с элементами

56

исходному изображению осуществляется с помощью обратного ортогонального преобразования

Периодограммы для упорядоченных по обобщенным пространственным частотам преобразований могут использоваться как для получения признаков изображений, так и для построения оценок спектральных плотностей двумерных случайных полей.

Для ДПФ справедлива теорема об автокорреляции. Эта теорема является дискретным аналогом теоремы об автокорреляции интегрального преобразования Фурье. Однако мы будем отдавать себе отчет в том, что в

57

отличие от интегрального преобразования Фурье, ДПФ от спектральной плотности, оценкой которой является периодограмма, дает не арифметическую автокорреляцию, а циклическую, т. е. автокорреляцию сигнала (изображения), периодически продолженного за его пределы. ДПФ от периодограммы будем считать оценкой автокорреляции цифрового изображения f j1 , j2

спектральных характеристик можно рассматривать непосредственно обобщенную периодограмму (4.8). Однако, IT u1 , u2 – нестабильные функции

обобщенных частот. Поэтому в качестве признаков предпочтительнее использовать интегральные характеристики, получаемые при их усреднении обобщенного спектра в областях специальной формы. Для формирования таких областей введем декартову и полярную системы координат в плоскости обобщенных пространственных частот, причем начало координат поместим в точку u1 0, u2 0 . В зависимости от вида преобразования начало координат

обобщенной периодограммы будет находиться либо в центре массива преобразования (Фурье, Хартли), либо в левом верхнем углу (косинусное и синусное преобразование).

Как и в случае спектрального анализа на основе преобразования Фурье,

интегральной частотной характеристикой (ОИЧХ), получается в результате суммирования значений IT u, в пределах каждой из кольцевых зон ( k -

номер кольца, k 1,...,K ). Характеристика ST l , которую назовем обобщенной

интегральной пространственной характеристикой (ОИПХ), вычисляется как сумма значений IT u, в пределах растра каждого из секторов ( l - номер

сектора, l 1,...,L ). С каждым кольцом ОИЧХ можно связать некоторый средний обобщенный пространственный период и говорить о безотносительном к ориентации распределении неоднородностей на изображении «по размерам».

58

По ОИПХ можно количественно оценивать анизотропию анализируемой на изображении структуры.

ориентации которых в плоскости частот диаметрально противоположны. Несколько большие вычислительные ресурсы требуются для точного вычисления периодограмм I F u1 , u2 изображений (а также ИЧХ и ИПХ) на

основе преобразования Хартли (или Q – преобразования) из соотношения:

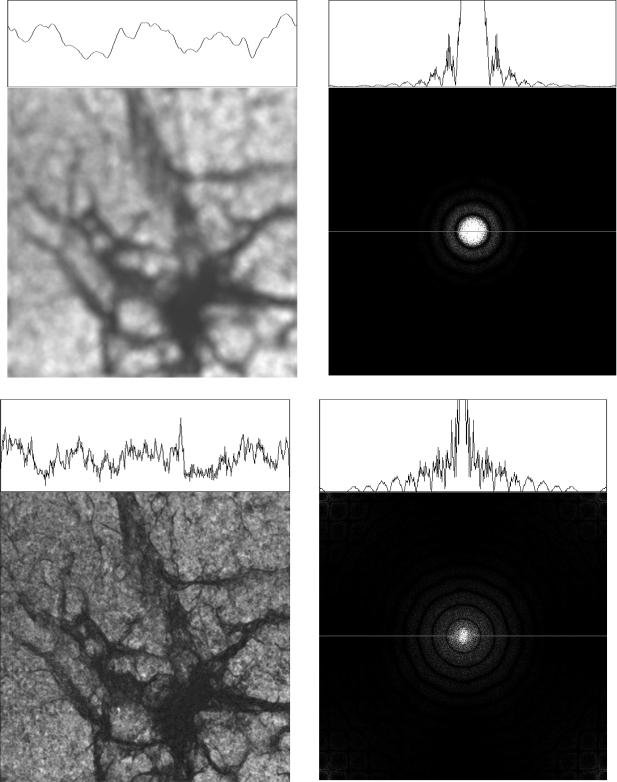
На рис. 4.1, а, б иллюстрируются результаты спектрального анализа на

основе преобразования Хартли электронно-микроскопического изображения аморфной пленки. В спектре достаточно четко проявляется анизотропный квазиволновой характер исходной структуры. В ИЧХ VH k можно выделить

базовую частотную моду (k 40) , а ИПХ S H l подтверждает наличие в спектре двух выделенных «осей анизотропии».

Рис. 4.1. Обобщенный спектральный анализ изображений

59

Спектральный анализ на основе преобразования Фурье также может применяться при идентификации корреляционно-спектральных характеристик стохастической микроструктуры различных сред и материалов по их электронно-оптическим изображениям. Данная процедура состоит в нахождении при выбранном аналитическом виде спектральной плотности (корреляционной функции) таких значений ее параметров, которые обеспечивают наилучшую аппроксимацию рассчитанных по изображению оценок либо спектральной плотности, либо корреляционной функции.

Оценки корреляционной функции B j1 , j2 можно получить исходя из

использованием соотношения (4.11).

Применение для спектрального анализа вместо преобразования Фурье рассмотренных выше унитарных преобразований позволяет сократить время расчетов и увеличить размеры обрабатываемых изображений. В операционной системе MS Windows время расчетов может быть уменьшено в среднем в 1,3 – 1,6 раза (в зависимости от преобразования и применяемых алгоритмов), а размеры обрабатываемых изображений увеличены, по меньшей мере, в 2 раза при заданном объеме оперативной памяти компьютера.

4.2.Обобщенная фильтрация изображений

Вданном разделе рассматривается применение рассмотренных выше унитарных преобразований для обобщенной фильтрации микроскопических изображений. Такая фильтрация во многих случаях оказывается более эффективной, чем пространственно-частотная фильтрация изображений на основе преобразования Фурье.

Большинство алгоритмов обработки дискретных изображений являются линейными: элементы обработанного изображения g n1 , n2 образуются в виде

j1 , j2 :

60