ВС для ГОС (ПИ) / Орлов, Цилькер - Организация ЭВМ (2004)

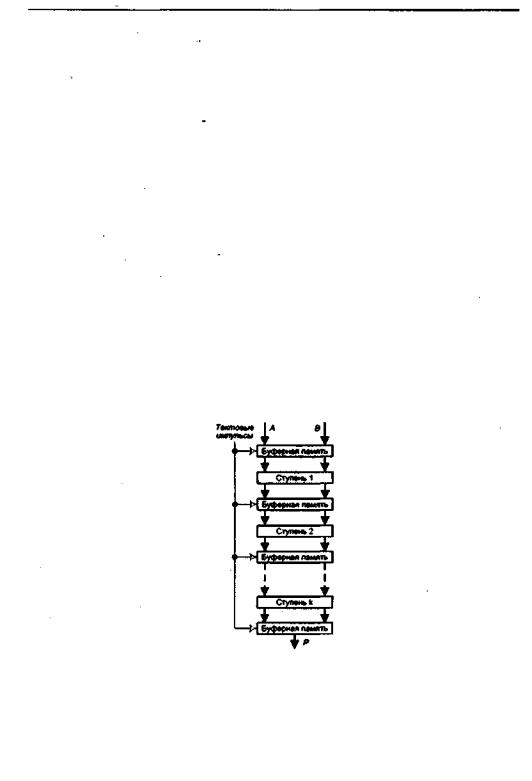
3 6 6 Глава 7. Операционные устройства вычислительных машин

Содержимое таблицы плюс некоторые не включенные в нее данные позволяют сделать следующие выводы. Наиболее быстро работают умножители, построенные по схеме Бута, а также имеющие древовидную структуру, в частности дерево Дадда. Для операндов длиной в 16 разрядов и более наиболее привлекательной представляется модифицированная схема Бута, как по скорости, так и по затратам оборудования. Максимально быстрое выполнение операции умножения обеспечивает сочетание алгоритма Бута и дерева Уоллеса. С другой стороны, достаточно хорошие показатели скорости при умножении чисел небольшой разрядности выдает схема Бо-Вули. В плане потребляемой мощности наиболее экономичными являются умножители, построенные по схемам Брауна и Пезариса. Несмотря на сравнительно небольшое число используемых транзисторов, схемы на базе алгоритма Бута, а также древовидные реализации, потребляют больше из-за избыточных внутренних связей, связанных с нерегулярной структурой этих схем.

Конвейеризация параллельных умножителей

В матричной и древовидной структурах параллельных умножителей заложен еще один потенциал повышения производительности — возможностьконвейеризации. При конвейеризации весьпроцесс вычислений разбивается напоследовательность законченных шагов. Каждый из этапов процедуры умножения выполняется на своей ступени конвейера, причем все ступени работают параллельно. Результаты, полученные на i-й ступени, передаются на дальнейшую обработку в (i + 1)-ю ступень конвейера. Перенос информации со ступени на ступень происходит через буферную память, размещаемую между ними (рис. 7.43).

Рис. 7.43. Структура конвейерногоумножителя

Выполнившая свою операцию ступень помещает результат в буферную память и может приступать к обработке следующей порции данных операций, в то время как очередная ступень конвейера в качестве исходных использует данные, хранящиеся в буферной памяти на ее входе. Синхронность работы конвейера обеспечивается тактовыми импульсами, период которых т определяется самой медленной

Ускорение целочисленного умножения 3 6 7

ступенью конвейера ti и задержкой в элементе буферной памяти ti t= max (t1 ,t2,

... tk) + ti. Несмотря на то что время выполнения операции умножения для каждой конкретной пары сомножителей в конвейерном умножителе не только не уменьшается, но даже несколько увеличивается за счет задержек в буферной памяти при последовательном перемножении последовательностей пар сомножителей, достигаемый выигрыш весьма ощутим. Действительно, в конвейерном умножителе из k ступеней перемножаемые данные могут подаваться на вход с интервалом в к раз меньшим, чем в случае обычного умножителя. В том же темпе появляются и результаты на выходе.

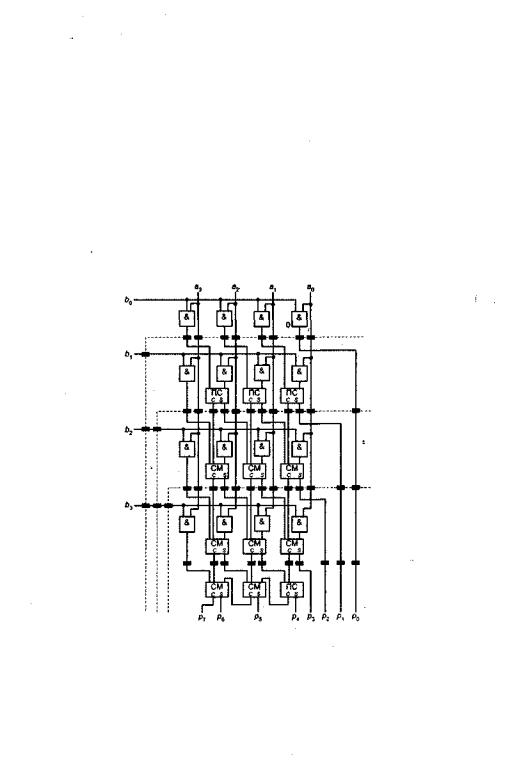
Схема конвейера легко может быть применена к матричным и древовидным умножителям. В матричных умножителях в качестве ступени конвейера выступает каждая строка матрицы сумматоров. В качестве примера конвейеризированного матричного умножителя на рис. 7,44 приведена схема 4x4. Черными прямоугольниками обозначены триггеры-защелки, образующие буферную память.

Рис. 7.44. Конвейеризированный матричный умножитель

Конвейеризация матричных умножителей на уровне строк сумматоров может быть затруднительной из-за большого числа ступеней и необходимости введения в состав умножителя значительного количества триггеров-защелок. Сокращение числа триггеров достигается за счет следующих приемов:

-отказа от использования идеи конвейеризации между входными схемами "И"

ипервой строкой полных сумматоров;

3 7 0 Глава 7. Операционные устройства вычислительных машин

Целочисленное деление

Деление несколько более сложная операция, чем умножение, но базируется на тех же принципах. Основу составляет общепринятый способ деления с помощью операций вычитания или сложения и сдвига (рис. 7.47).

Рис. 7.47. Общая схема операции деления

Задача сводится к вычислению частного Q и остатка S:

Деление выражается как последовательность вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков (40).

Операция выполняется за л итераций и можетбыть описана следующим образом:

После п итераций получается

Частное от деления 2n-разрядного числа на n-разрядное может содержать более, чем п разрядов. В этом случае возникает переполнение, из-за чего перед выполнением деления необходима проверка условия

Из выражения следует, что переполнения не будет, если число, содержащееся в старших п разрядах делимого, меньше делителя.

Помимо этого требования, перед началом операции необходимо исключить возможность ситуации деления на 0.

Реализовать деление можно двумя основными способами: - с неподвижным делимым и сдвигаемым вправо делителем; я с неподвижным делителем и сдвигаемым влево делимым.

Недостатком первого способа является потребность иметь в устройстве деления сумматор и регистр двойной длины. Второй способ позволяет строить дели-

тель с сумматором одинарной длины. Неподвижный делитель D хранится в регистре одинарной длины, а делимое Z, сдвигаемое относительно D, находится в двух таких же регистрах. Образующиеся цифры частного Q заносятся в освобождающиеся при сдвиге Zразряды одного из регистров Z

Ниже на. примере чисел без знака рассматриваются два основных алгоритма целочисленного деления.

Деление с восстановлением остатка

Наиболее очевидный алгоритм носит название алгоритма деления с неподвижным делителем и восстановлением остатка. В учебнике он представлен в силу того, что очень похож на общепринятый способ деления столбиком. Данный алгоритм может быть описан следующим образом:

1.Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2.Частичный остаток удваивается путем сдвига на один разряд влево. При этом

восвобождающийся при сдвиге младший разряд 40 заносится очередная цифра частного.

3.Из сдвинутого Ч0 вычитается делитель и анализируется знак результата вычитания.

4.Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и нулю, если отрицателен. В последнем случае значение остатка восстанавливается до того значения, которое было до вычитания.

5.Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

На рис. 7,48 показан процесс деления с восстановлением остатка, здесь число 41 делится на 8.

Деление без восстановления остатка

Недостаток затронутого алгоритма заключается в необходимости выполнения на отдельных шагах дополнительных операций сложения для восстановления частичного остатка. Это увеличивает время выполнения деления, которое в этом случае может меняться в зависимости от конкретного сочетания кодов операндов. В силу указанных причин реальные делители строятся на основе алгоритма деленияснеподвижнымделителембезвосстановленияостатка.Приведемописание этого алгоритма.

1, Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2, Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разрядЧ0 заносится очередная цифра частного.

3, Из сдвинутого частичного остатка вычитается делитель, если остаток положителен, и к сдвинутому частичному остатку прибавляется делитель, если остаток отрицательный.

3 7 2 Глава 7. Операционныеустройствавычислительных машин

Рис. 7,48. Пример деления с восстановлением остатка

4.Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и нулю, если он отрицателен.

5.Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

Как видим, пункты 1,2,5 полностью совпадают с соответствующими пунктами предыдущего алгоритма деления.

Процесс деления без восстановления остаткадля ранее рассмотренного примера демонстрируется на рис. 7.49.

Деление чисел со знаком

Как и в случае умножения, деление чисел со знаком может быть выполнено путем перехода к абсолютным значениям делимого и делителя, с последующим присвоением частному знака «плюс» при совпадающих знаках делимого и делителя либо «минус» — в противном случае.

Деление чисел, представленных в дополнительном коде, можно осуществлять не переходя к модулям. Рассмотрим необходимые для этого изменения в алгоритме без восстановления остатка.

Так как делимое и делитель не обязательно имеют одинаковые знаки, то действия с частичным остатком (прибавление или вычитание D) зависят от знаков остатка и делителя и определяются содержимым табл. 7,5:

Целочисленное деление 3 7 3

Рис.7.49. Примерделения без восстановления остатка

И Если знак остатка совпадает со знаком делителя, то очередная цифра частного — 1, иначе — 0.

- Ecли Z>0 и D< 0, частное необходимо увеличить на 1.

-Если Z < 0 и D > 0, то при ненулевом остатке от деления частное нужно увеличить на единицу.

-Если Z < 0 и D < 0, то при нулевом остатке от деления частное нужно увеличить на единицу.

Остаток всегда приводится к положительному числу, то есть если по завершении деления он отрицателен, к нему следует прибавить модуль делителя.

Устройство деления

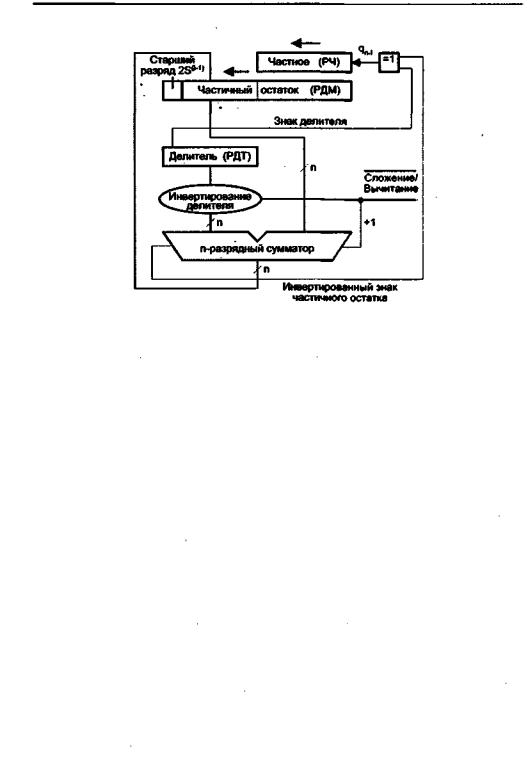
Рассмотренный алгоритм деления без восстановления остатка может быть реализован с помощью устройства, схема которого приведена на рис. 7.50.

Процедура начинается с занесения делимого в 2n-разрядный регистр делимого (РДМ) иделителя вn-разрядныйрегистрделителя(РДТ). Всчетчикцикла(СЧЦ — на схеме не показан), служащий для подсчета количества полученных цифр частного, помещается исходное значение, равное п.

3 7 4 Глава7. Операционныеустройства вычислительных машин

Рис.7.50.Схемаделенияпоалгоритмубезвосстановленияостатка

На каждом шаге содержимое регистра делимого (РДМ) и регистра частного (РЧ)сдвигаетсянаодинразрядвлево.Взависимостиотсочетаниязнаковчастичного остатка и делителя определяется значение очередной цифры частного и требуемое действие: вычитание или прибавлениеделителя. Вычитаниеделителяпроизводится посредством прибавления дополнительного кода делителя. Преобразование в дополнительный код осуществляется за счет передачи делителя на вход сумматораобратным (инверсным)кодомс последующимдобавлением единицы кмлад-- шему разряду сумматора.

Описанная процедура повторяется до исчерпания всех цифр делимого, о чем свидетельствует нулевое содержимое счетчика циклов (содержимое СЧЦ уменьшается на единицу после каждой итерации). По окончании операции деления частное располагается в регистре частного, а в регистре делимого будет остаток от деления.

На заключительном этапе, если это необходимо, производится корректировка полученногорезультата, какэтопредусматриваеталгоритмделения чисел сознаком.

На практике для накопления и хранения частного вместо отдельного регистра используют освобождающиеся в процессе сдвигов младшие разряды регистра делимого.

Комбинированноеустройствоумножения/деления

Сходство процедур умножения иделения находитсвое отражение в близости структур соответствующих устройств (рис. 7.51).

Из подобия процедур вытекает очевидная идея реализации обеих операций с помощью единых технических средств, в виде комбинированного устройства ум- ножения-деления (рис. 7.52).