
- •Замечательные точки в треугольнике .
- •Средняя линия в треугольнике и ее свойства. Теорема Вариньона. Площади. [7,8,9].
- •Подсчет углов. Вписанный угол. Угол между хордами и секущими к окружности. Угол между касательной и хордой. [7,8,9].
- •Вписанный четырехугольник. Критерии вписанного четырехугольника (5 признаков). [7,8,9]
- •Теорема о касательной и секущей. [7,8,9]
- •Теорема Фалеса с доказательством. Теорема о пропорциональных отрезках. [7,8,9]
- •Лемма Мансиона и ее обобщение. [7,8,9]
- •Окружность Эйлера 9 точек. [7,8,9]
- •Прямая Симпсона. [7,8,9]
- •Теорема Птолемея. [7,8,9,10]
- •Теорема Чевы и ее обобщение. Обратная теорема Чевы. [7,8,9]
- •Теорема Менелая и ее обобщение. Обратная теорема Менелая. [7,8,9]
- •Тригонометрическая форма теоремы Чевы. Изотомическое и изогональное сопряжение. Доказать, что точки и изогонально сопряжены. Точка Лемуана. [7,8,9,12]
- •Гомотетия, свойства гомотетии. Теорема Эйлера о том, что точки лежат на одной прямой, причем . [7,8,9]
- •Вневписанные окружности. Точка Нагеля . Свойства нагелиан. Доказать, что точки и изотомически сопряжены. [7,8,9]
- •Теорема Архимеда о двух касающихся окружностях. Задача Архимеда о ломаной.[5,12]
- •Теорема о прямой Эйлера-Нагеля. Доказать, что , .[5]
- •Степень точки относительно окружности. Радикальная ось двух окружностей. Радикальный центр трех окружностей.[4,5,7,8,9]
- •Формула Эйлера для вычисления расстояния между центрами вписанной и описанной окружности. [7,8,9]
- •Точка Торричелли и ее свойства.[3,4,5]
- •Треугольник наименьшего периметра, вписанный в данный треугольник. [3,4,5]
- •Теорема Брианшона. [3,4,5,7,8]
- •Окружность, вписанная в сегмент и ее свойства.[5]
- •Лемма о бабочке.[10, задача 122]
- •Понятие центра масс системы материальных точек. Существование, единственность, группировка с доказательством. Теорема о центроиде четырехугольника.[1,2,5,12]
- •Доказать с помощью понятия центра масс, что медианы (биссектрисы, высоты) пересекаются в одной точке и найти пропорцию, в которой точка пересечения делит соответствующую линию. [1,2,5,12]
- •Понятие барицентрических координат точки относительно треугольника . Найти барицентрические координаты точек: середины , центров вневписанных окружностей. [1,2,5,12]
- •Условие принадлежности одной прямой трех точек с заданными барицентрическими координатами. Уравнение прямой линии в барицентрических координатах. [1,2,5,12]
- •Признак ромба: если радиусы окружностей, вписанных в треугольники, образуемые сторонами и диагоналями четырехугольника, равны, то этот четырехугольник – ромб.
- •Теорема о биссектрисах внешних углов полного четырехугольника.
- •Теорема о трех центрах гомотетий (о трех колпаках).[7]
- •Инверсия относительно окружности. Деление отрезка пополам с помощью одного циркуля. Стереографическая проекция.[7]
- •Полярное соответствие. Свойство взаимности поляр. Двойственность в геометрии. Теорема Паскаля. [7]
- •Векторы и комплексные числа.
- •Разное.
- •Литература по курсу элементарная математика (геометрия)
-
Вневписанные окружности. Точка Нагеля . Свойства нагелиан. Доказать, что точки и изотомически сопряжены. [7,8,9]
-
Пусть
 - точки касания вписанной и вневписанной
окружностей со стороной
- точки касания вписанной и вневписанной
окружностей со стороной
 ;
обозначим ближайшую к вершине
;
обозначим ближайшую к вершине точку пересечения прямой
точку пересечения прямой
 с вписанной окружностью через
с вписанной окружностью через
 .
Доказать:
.
Доказать:
a)
![]() ;
;
b)
![]() - диаметр вписанной окружности;
- диаметр вписанной окружности;
c) прямые
![]() пересекаются в одной точке. Эта точка
называется точкой Нагеля треугольника
пересекаются в одной точке. Эта точка
называется точкой Нагеля треугольника
![]() .
.
2. Доказать, что точки
![]() и
и
![]() изотомически сопряжены.
изотомически сопряжены.
-
Теорема Архимеда о двух касающихся окружностях. Задача Архимеда о ломаной.[5,12]
-
Хорда
 разбивает окружность
разбивает окружность
 на две дуги. Окружность
на две дуги. Окружность
 касается хорды
касается хорды
 в точке
в точке
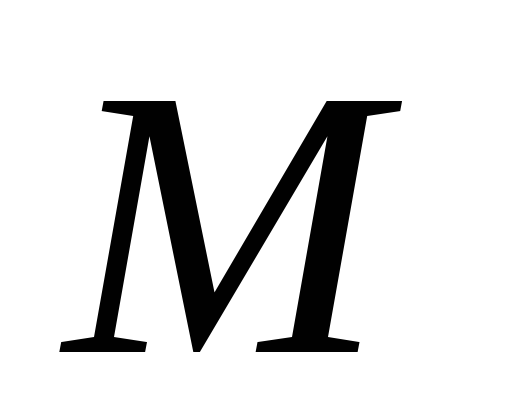 и одной из дуг в точке
и одной из дуг в точке
 .
Доказать, что
.
Доказать, что
 - биссектриса треугольника
- биссектриса треугольника
 .
. -
На окружности
 выбраны точки
выбраны точки
 .
Из середины
.
Из середины
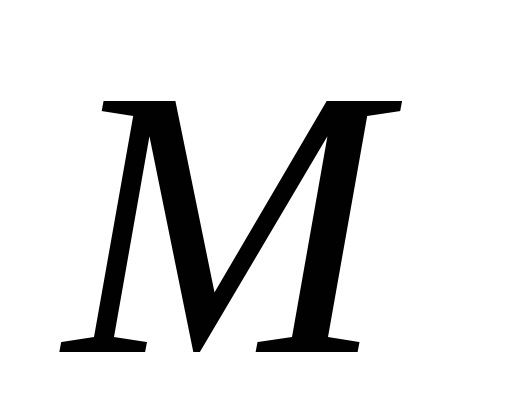 дуги
дуги
 ,
содержащей
,
содержащей
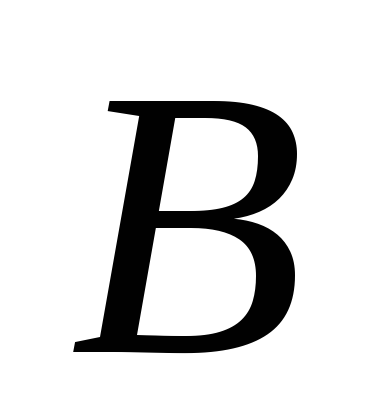 ,
опущен перпендикуляр
,
опущен перпендикуляр
 на отрезок
на отрезок
 .
Доказать, что
.
Доказать, что
 .
.
-
Теорема о прямой Эйлера-Нагеля. Доказать, что , .[5]
-
В треугольник
 вписана окружность
вписана окружность
 .
Точки касания
.
Точки касания
 со сторонами
со сторонами
 и
и
 обозначены,
соответственно, через
обозначены,
соответственно, через
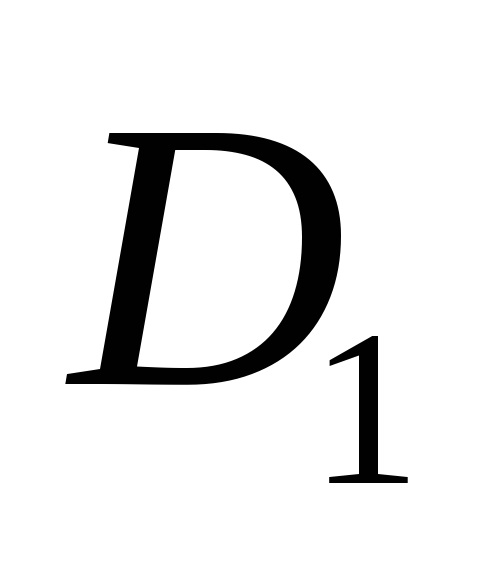 и
и
 .
На сторонах
.
На сторонах
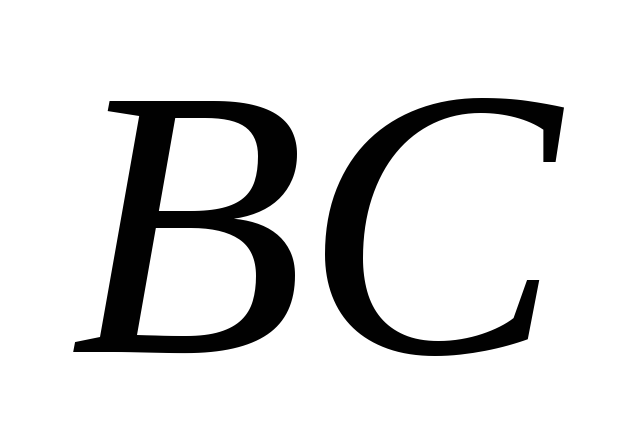 и
и
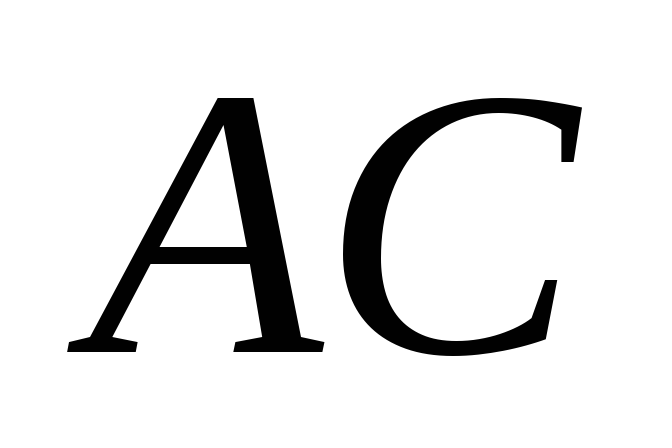 отмечены также точки
отмечены также точки
 и
и
 ,
соответственно, для которых
,
соответственно, для которых
 и
и
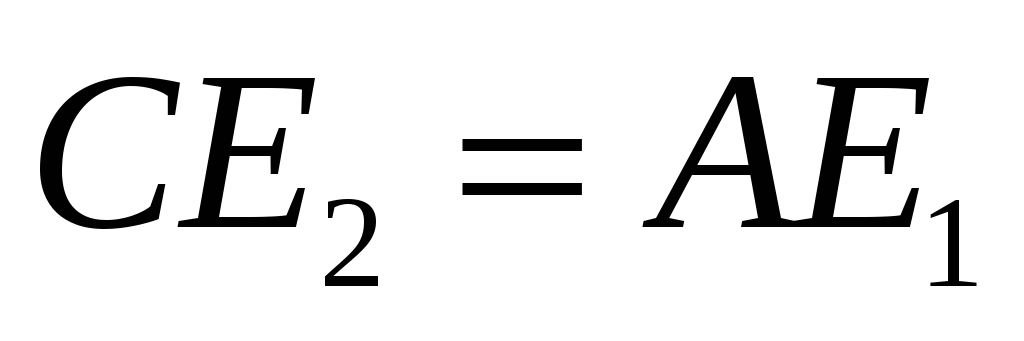 .
Пусть
.
Пусть
 - точка пересечения отрезков
- точка пересечения отрезков
 и
и
 ,
и
,
и
 - ближайшая к вершине
- ближайшая к вершине
 точка пересечения окружности
точка пересечения окружности
 и отрезка
и отрезка
 .
Доказать, что
.
Доказать, что
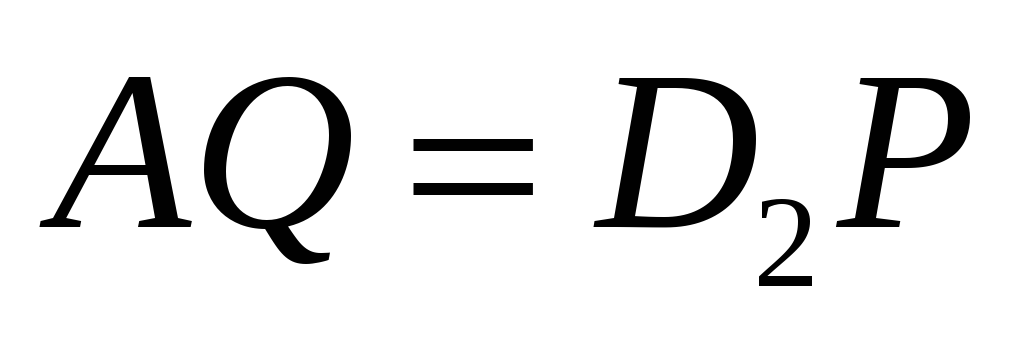 .
. -
Пусть
 - центры вписанной, описанной окружности,
точка пересечения медиан и точка Нагеля
треугольника. Доказать, что
- центры вписанной, описанной окружности,
точка пересечения медиан и точка Нагеля
треугольника. Доказать, что
 ,
,
 .
.
-
Степень точки относительно окружности. Радикальная ось двух окружностей. Радикальный центр трех окружностей.[4,5,7,8,9]
-
Пусть
 - окружность с центром в точке
- окружность с центром в точке
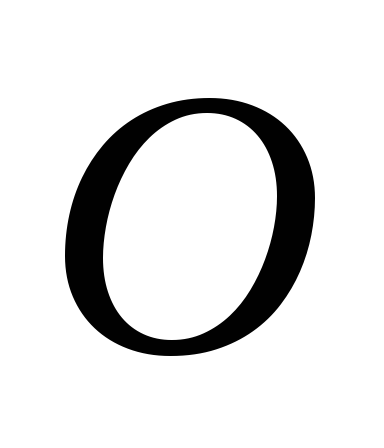 и радиусом
и радиусом
 .
Степенью точки
.
Степенью точки
 относительно
относительно
 называется число
называется число
 ,
где
,
где
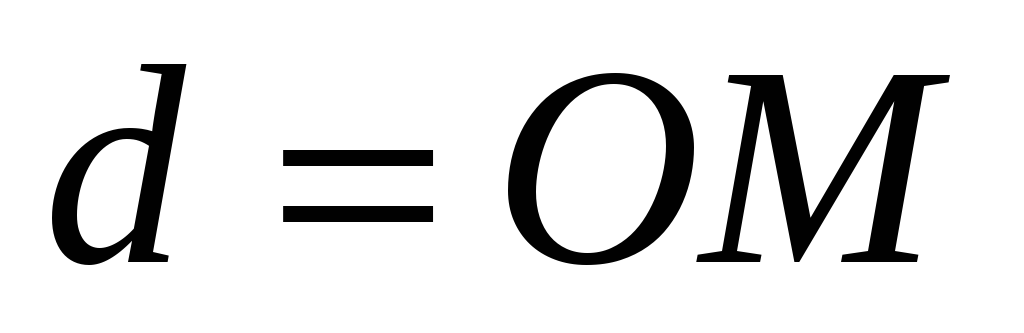 .
Для каких точек плоскости степень
положительна, отрицательна, равна нулю?
.
Для каких точек плоскости степень
положительна, отрицательна, равна нулю? -
На плоскости дана окружность
 и точка
и точка
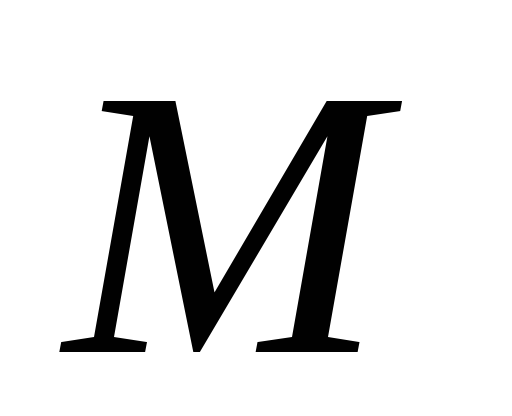 .
Прямая, проведенная через точку
.
Прямая, проведенная через точку
 ,
пересекает окружность в точках
,
пересекает окружность в точках
 и
и
 .
Докажите, что произведение
.
Докажите, что произведение
 не зависит от выбора прямой. Эта величина,
взятая со знаком плюс для точки
не зависит от выбора прямой. Эта величина,
взятая со знаком плюс для точки
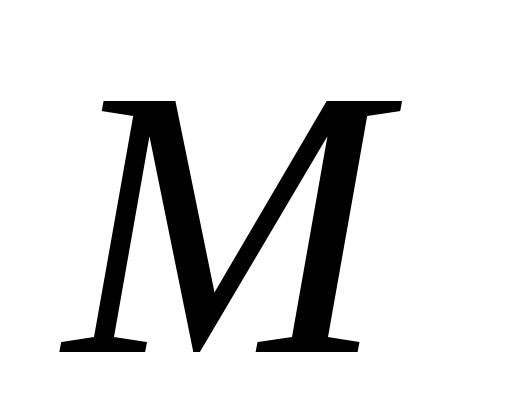 вне окружности и со знаком минус для
точки
вне окружности и со знаком минус для
точки
 внутри окружности, равна степени точки
внутри окружности, равна степени точки
 относительно
относительно
 .
. -
Пусть
 и
и
 - две не концентрические окружности.
Множество точек
- две не концентрические окружности.
Множество точек
 на плоскости, имеющих одинаковые степени
относительно окружностей
на плоскости, имеющих одинаковые степени
относительно окружностей
 и
и
 ,
называется радикальной осью этих
окружностей. Доказать, что радикальная
ось двух окружностей – прямая,
перпендикулярная линии центров.
,
называется радикальной осью этих
окружностей. Доказать, что радикальная
ось двух окружностей – прямая,
перпендикулярная линии центров.
-
Доказать, что радикальная ось двух пересекающихся окружностей – это прямая, проходящая через точки пересечения этих окружностей, а радикальная ось двух касающихся окружностей – это общая касательная этих окружностей.
-
Доказать, что точка
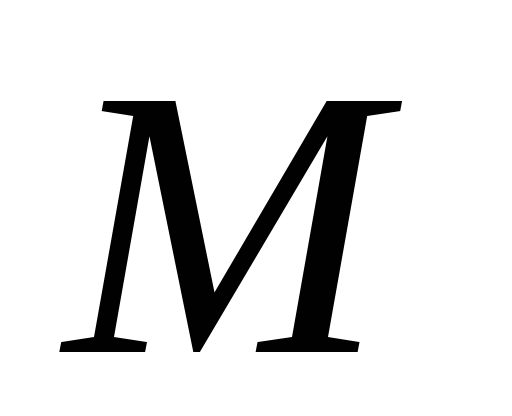 ,
лежащая вне окружностей
,
лежащая вне окружностей
 и
и
 ,
лежит на радикальной оси этих окружностей
тогда и только тогда, когда длины
касательных, проведенных из
,
лежит на радикальной оси этих окружностей
тогда и только тогда, когда длины
касательных, проведенных из
 к этим окружностям равны.
к этим окружностям равны. -
Вершины прямоугольника
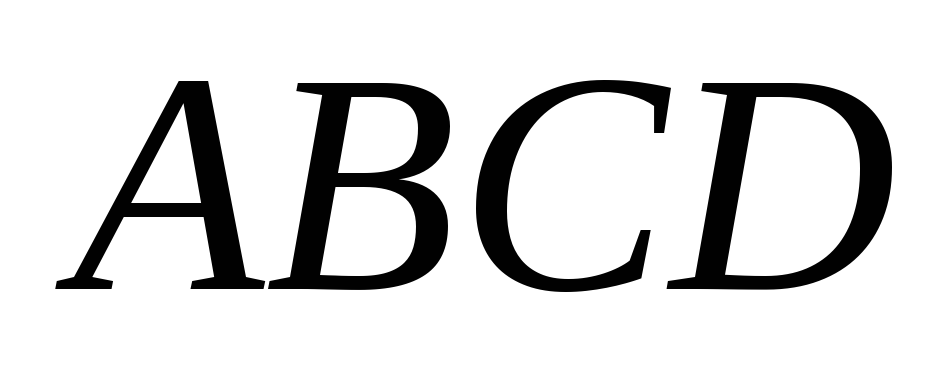 лежат на двух пересекающихся окружностях:
точки
лежат на двух пересекающихся окружностях:
точки и
и
 лежат на
лежат на
 ,
точки
,
точки и
и
 лежат на
лежат на
 .
Доказать, что точка пересечения
диагоналей
.
Доказать, что точка пересечения
диагоналей
 лежит на отрезке, соединяющем точки
пересечения окружностей
лежит на отрезке, соединяющем точки
пересечения окружностей
 и
и
 .
. -
Пусть
 ,
,
 и
и
 -
три окружности, центры которых не лежат
на одной прямой. Докажите, что попарные
радикальные оси этих окружностей
пересекаются в одной точке. Эта точка
называется радикальным центром трех
окружностей
-
три окружности, центры которых не лежат
на одной прямой. Докажите, что попарные
радикальные оси этих окружностей
пересекаются в одной точке. Эта точка
называется радикальным центром трех
окружностей
 ,
,
 и
и
 .
. -
Постройте с помощью циркуля и линейки радикальную ось окружности и точки, считая точку окружностью нулевого радиуса. Что такое радикальная ось для двух точек? Что такое радикальный центр для трех точек?
-
Постройте с помощью циркуля и линейки радикальную ось двух окружностей.
-
В треугольнике
 из вершин на противоположные стороны
проведены шесть отрезков одинаковой
длины (по два из каждой вершины). Докажите,
что середины этих шести отрезков лежат
на одной окружности
из вершин на противоположные стороны
проведены шесть отрезков одинаковой
длины (по два из каждой вершины). Докажите,
что середины этих шести отрезков лежат
на одной окружности -
Дан остроугольный треугольник ABC. Касательные, проведенные из A к окружности, построенной на BC как на диаметре, касаются окружности в точках P и Q. Докажите, что точки P, Q, H (H - ортоцентр треугольника ABC) лежат на одной прямой. Р
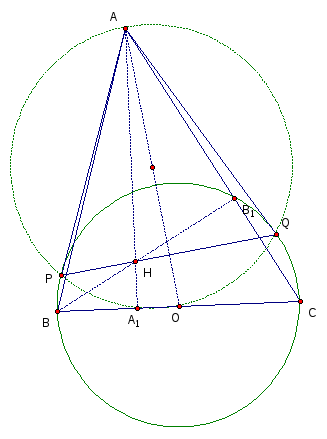 ешение.
Обозначим через
ешение.
Обозначим через
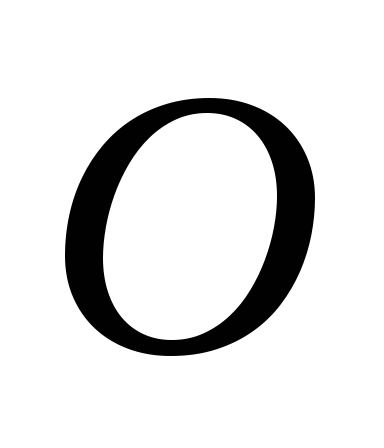 - центр окружности
- центр окружности
 с диаметром АС. Построим также окружность
с диаметром АС. Построим также окружность
 с диаметром АО. Прямая
с диаметром АО. Прямая
 является радикальной ось этих двух
окружностей. Проверим, что точка Н имеет
одинаковую степень относительно этих
окружностей, т.е. лежит на радикальной
оси. Пусть
является радикальной ось этих двух
окружностей. Проверим, что точка Н имеет
одинаковую степень относительно этих
окружностей, т.е. лежит на радикальной
оси. Пусть
 - высоты треугольника АВС, проведенные
из вершин
- высоты треугольника АВС, проведенные
из вершин
 и
и
 ,
соответственно. Степень точки Н
относительно
,
соответственно. Степень точки Н
относительно
 равна
равна
 ,
а относительно
,
а относительно

 ,
но точки
,
но точки
 лежат на окружности с диаметром АВ.
Поэтому
лежат на окружности с диаметром АВ.
Поэтому
 и значит
и значит
 .
. -
