
- •Замечательные точки в треугольнике .
- •Средняя линия в треугольнике и ее свойства. Теорема Вариньона. Площади. [7,8,9].
- •Подсчет углов. Вписанный угол. Угол между хордами и секущими к окружности. Угол между касательной и хордой. [7,8,9].
- •Вписанный четырехугольник. Критерии вписанного четырехугольника (5 признаков). [7,8,9]
- •Теорема о касательной и секущей. [7,8,9]
- •Теорема Фалеса с доказательством. Теорема о пропорциональных отрезках. [7,8,9]
- •Лемма Мансиона и ее обобщение. [7,8,9]
- •Окружность Эйлера 9 точек. [7,8,9]
- •Прямая Симпсона. [7,8,9]
- •Теорема Птолемея. [7,8,9,10]
- •Теорема Чевы и ее обобщение. Обратная теорема Чевы. [7,8,9]
- •Теорема Менелая и ее обобщение. Обратная теорема Менелая. [7,8,9]
- •Тригонометрическая форма теоремы Чевы. Изотомическое и изогональное сопряжение. Доказать, что точки и изогонально сопряжены. Точка Лемуана. [7,8,9,12]
- •Гомотетия, свойства гомотетии. Теорема Эйлера о том, что точки лежат на одной прямой, причем . [7,8,9]
- •Вневписанные окружности. Точка Нагеля . Свойства нагелиан. Доказать, что точки и изотомически сопряжены. [7,8,9]
- •Теорема Архимеда о двух касающихся окружностях. Задача Архимеда о ломаной.[5,12]
- •Теорема о прямой Эйлера-Нагеля. Доказать, что , .[5]
- •Степень точки относительно окружности. Радикальная ось двух окружностей. Радикальный центр трех окружностей.[4,5,7,8,9]
- •Формула Эйлера для вычисления расстояния между центрами вписанной и описанной окружности. [7,8,9]
- •Точка Торричелли и ее свойства.[3,4,5]
- •Треугольник наименьшего периметра, вписанный в данный треугольник. [3,4,5]
- •Теорема Брианшона. [3,4,5,7,8]
- •Окружность, вписанная в сегмент и ее свойства.[5]
- •Лемма о бабочке.[10, задача 122]
- •Понятие центра масс системы материальных точек. Существование, единственность, группировка с доказательством. Теорема о центроиде четырехугольника.[1,2,5,12]
- •Доказать с помощью понятия центра масс, что медианы (биссектрисы, высоты) пересекаются в одной точке и найти пропорцию, в которой точка пересечения делит соответствующую линию. [1,2,5,12]
- •Понятие барицентрических координат точки относительно треугольника . Найти барицентрические координаты точек: середины , центров вневписанных окружностей. [1,2,5,12]
- •Условие принадлежности одной прямой трех точек с заданными барицентрическими координатами. Уравнение прямой линии в барицентрических координатах. [1,2,5,12]
- •Признак ромба: если радиусы окружностей, вписанных в треугольники, образуемые сторонами и диагоналями четырехугольника, равны, то этот четырехугольник – ромб.
- •Теорема о биссектрисах внешних углов полного четырехугольника.
- •Теорема о трех центрах гомотетий (о трех колпаках).[7]
- •Инверсия относительно окружности. Деление отрезка пополам с помощью одного циркуля. Стереографическая проекция.[7]
- •Полярное соответствие. Свойство взаимности поляр. Двойственность в геометрии. Теорема Паскаля. [7]
- •Векторы и комплексные числа.
- •Разное.
- •Литература по курсу элементарная математика (геометрия)
-
Подсчет углов. Вписанный угол. Угол между хордами и секущими к окружности. Угол между касательной и хордой. [7,8,9].
-
Доказать, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
-
Доказать, что угол между биссектрисами смежных углов прямой.
-
Найти сумму углов пятиконечной звезды, не обязательно правильной.
-
Доказать, что биссектриса прямого угла треугольника делит пополам угол между медианой и высотой этого угла.
-
В прямоугольнике

 .
Сторона
.
Сторона
 точками
точками
 и
и
 делится на три равные части. Найти сумму
углов
делится на три равные части. Найти сумму
углов
 .
. -
На сторонах
 и
и
 треугольника
треугольника
 ,
во внешнюю сторону построены равнобедренные
треугольники
,
во внешнюю сторону построены равнобедренные
треугольники
 и
и
 ,
причем
,
причем
 .
Пусть
.
Пусть
 - середина отрезка
- середина отрезка
 .
Доказать, что
.
Доказать, что
 .
. -
На стороне
 треугольника
треугольника
 отметили точки
отметили точки
 и
и
 так, что
так, что
 и
и
 .
Докажите, что отрезок
.
Докажите, что отрезок
 виден из середины
виден из середины
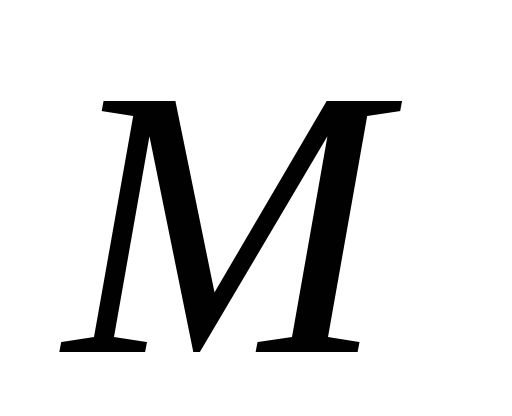 стороны
стороны
 под прямым углом.
под прямым углом. -
Доказать, что вписанный угол, опирающийся на дугу
 окружности равен половине центрального
угла, опирающегося на эту дугу.
окружности равен половине центрального
угла, опирающегося на эту дугу.
-
Доказать, что вписанный угол прямой тогда и только тогда когда он опирается на диаметр.
-
Хорды
 и
и
 окружности
окружности
 параллельны. Доказать, что
параллельны. Доказать, что
 .
. -
Найти на плоскости множество точек, из которых данный отрезок виден под углом
 .
Постройте это множество с помощью
циркуля и линейки.
.
Постройте это множество с помощью
циркуля и линейки. -
Доказать, что касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
-
Доказать, что длины двух касательных к окружности, проведенных из одной точки, равны.
-
Две окружности пересекаются в точках
 и
и
 .
Третья окружность с центром в точке
.
Третья окружность с центром в точке
 пересекает первую в точках
пересекает первую в точках
 ,
а вторую – в точках
,
а вторую – в точках
 .
Докажите, что углы
.
Докажите, что углы
 и
и
 равны.
равны. -
В выпуклом пятиугольнике
 все стороны равны, а угол
все стороны равны, а угол
 в два раза больше угла
в два раза больше угла
 .
Найти угол
.
Найти угол
 .
.
Решение.
 Отразим
точки
Отразим
точки
![]() и
и
![]() относительно
относительно
![]() и
и
![]() ,
соответственно, получим равносторонний
треугольник
,
соответственно, получим равносторонний
треугольник
![]() .
Сумма углов
.
Сумма углов
![]() равна
равна
![]() .
Отсюда,
.
Отсюда,
![]() .
.
-
Пусть
 - вневписанная окружность треугольника
- вневписанная окружность треугольника
 ,
касающаяся стороны
,
касающаяся стороны
 в точке
в точке
 .
Доказать, что
.
Доказать, что
 .
. -
Пусть хорды
 и
и
 окружности пересекаются в точке
окружности пересекаются в точке
 .
Тогда угол
.
Тогда угол
 ,
где
,
где
 и
и

 -
величины дуг окружности, заключенных
между углами
-
величины дуг окружности, заключенных
между углами
 и
и
 .
Напомним, что величиной дуги окружности
называется величина центрального угла
опирающегося на эту дугу.
.
Напомним, что величиной дуги окружности
называется величина центрального угла
опирающегося на эту дугу. -
Пусть две секущие, проведенные из одной точки
 к окружности, пересекают ее в точках
к окружности, пересекают ее в точках
 и
и
 ,
соответственно. Тогда угол
,
соответственно. Тогда угол
 ,
где
,
где
 и
и

 -
большая и меньшая величины дуг окружности
внутри угла
-
большая и меньшая величины дуг окружности
внутри угла
 .
.
-
Доказать, что угол между касательной к окружности в точке
 и хордой
и хордой
 равен половине дуги окружности между
этой касательной и хордой
равен половине дуги окружности между
этой касательной и хордой
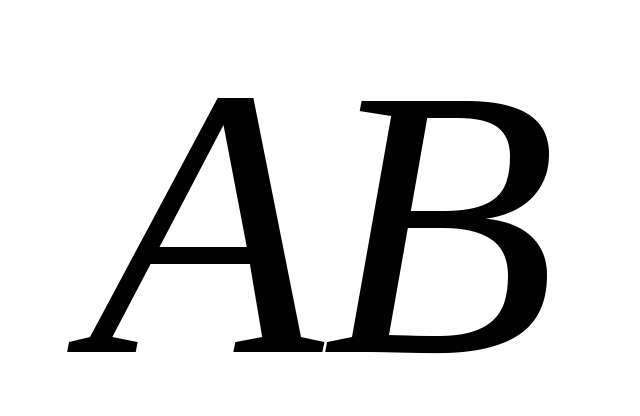 .
Сформулируйте и докажите также обратное
утверждение.
.
Сформулируйте и докажите также обратное
утверждение. -
Две окружности пересекаются в точках
 и
и
 .
Через точку
.
Через точку
 проведена прямая, пересекающая первую
окружность в точке
проведена прямая, пересекающая первую
окружность в точке
 ,
а вторую – в точке
,
а вторую – в точке
 .
Пусть
.
Пусть
 и
и
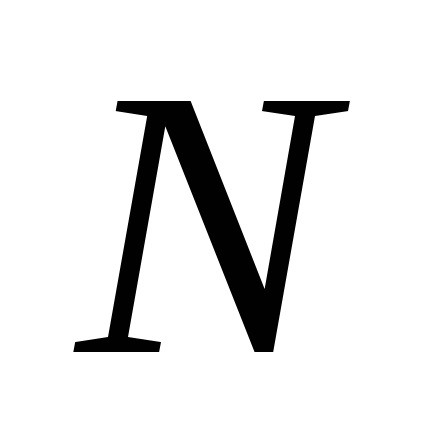 - середины дуг
- середины дуг
 и
и
 ,
не содержащих точку
,
не содержащих точку
 ,
а
,
а
 - середина отрезка
- середина отрезка
 .
Докажите, что угол
.
Докажите, что угол
 равен
равен
 .
(Можно считать, что точки
.
(Можно считать, что точки
 и
и
 лежат по разные стороны от точки
лежат по разные стороны от точки
 .
. -
Концы пяти параллельных хорд делят окружность на десять дуг. Известно, что для любой из этих дуг соседние с ней дуги равны между собой. Докажите, что сумма длин средней и двух крайних хорд равна сумме двух других хорд.
-
Через вершину
 треугольника
треугольника
 и основание биссектрисы угла
и основание биссектрисы угла
 проведена окружность
проведена окружность
 ,
пересекающая стороны
,
пересекающая стороны
 и
и
 в точках
в точках
 и
и
 .
Докажите, что если
.
Докажите, что если
 ,
то
,
то
 касается
касается
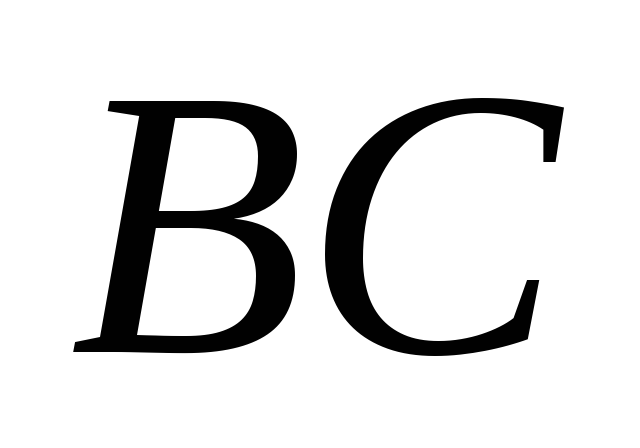 .
. -
В треугольнике
 проведена биссектриса
проведена биссектриса
 .
Через точку
.
Через точку
 к окружности, описанной около треугольника
к окружности, описанной около треугольника
 ,
проведена касательная, пересекающая
сторону
,
проведена касательная, пересекающая
сторону
 в точке
в точке
 .
Докажите, что прямая
.
Докажите, что прямая
 касается окружности, описанной около
треугольника
касается окружности, описанной около
треугольника
 .
.
