
- •Замечательные точки в треугольнике .
- •Средняя линия в треугольнике и ее свойства. Теорема Вариньона. Площади. [7,8,9].
- •Подсчет углов. Вписанный угол. Угол между хордами и секущими к окружности. Угол между касательной и хордой. [7,8,9].
- •Вписанный четырехугольник. Критерии вписанного четырехугольника (5 признаков). [7,8,9]
- •Теорема о касательной и секущей. [7,8,9]
- •Теорема Фалеса с доказательством. Теорема о пропорциональных отрезках. [7,8,9]
- •Лемма Мансиона и ее обобщение. [7,8,9]
- •Окружность Эйлера 9 точек. [7,8,9]
- •Прямая Симпсона. [7,8,9]
- •Теорема Птолемея. [7,8,9,10]
- •Теорема Чевы и ее обобщение. Обратная теорема Чевы. [7,8,9]
- •Теорема Менелая и ее обобщение. Обратная теорема Менелая. [7,8,9]
- •Тригонометрическая форма теоремы Чевы. Изотомическое и изогональное сопряжение. Доказать, что точки и изогонально сопряжены. Точка Лемуана. [7,8,9,12]
- •Гомотетия, свойства гомотетии. Теорема Эйлера о том, что точки лежат на одной прямой, причем . [7,8,9]
- •Вневписанные окружности. Точка Нагеля . Свойства нагелиан. Доказать, что точки и изотомически сопряжены. [7,8,9]
- •Теорема Архимеда о двух касающихся окружностях. Задача Архимеда о ломаной.[5,12]
- •Теорема о прямой Эйлера-Нагеля. Доказать, что , .[5]
- •Степень точки относительно окружности. Радикальная ось двух окружностей. Радикальный центр трех окружностей.[4,5,7,8,9]
- •Формула Эйлера для вычисления расстояния между центрами вписанной и описанной окружности. [7,8,9]
- •Точка Торричелли и ее свойства.[3,4,5]
- •Треугольник наименьшего периметра, вписанный в данный треугольник. [3,4,5]
- •Теорема Брианшона. [3,4,5,7,8]
- •Окружность, вписанная в сегмент и ее свойства.[5]
- •Лемма о бабочке.[10, задача 122]
- •Понятие центра масс системы материальных точек. Существование, единственность, группировка с доказательством. Теорема о центроиде четырехугольника.[1,2,5,12]
- •Доказать с помощью понятия центра масс, что медианы (биссектрисы, высоты) пересекаются в одной точке и найти пропорцию, в которой точка пересечения делит соответствующую линию. [1,2,5,12]
- •Понятие барицентрических координат точки относительно треугольника . Найти барицентрические координаты точек: середины , центров вневписанных окружностей. [1,2,5,12]
- •Условие принадлежности одной прямой трех точек с заданными барицентрическими координатами. Уравнение прямой линии в барицентрических координатах. [1,2,5,12]
- •Признак ромба: если радиусы окружностей, вписанных в треугольники, образуемые сторонами и диагоналями четырехугольника, равны, то этот четырехугольник – ромб.
- •Теорема о биссектрисах внешних углов полного четырехугольника.
- •Теорема о трех центрах гомотетий (о трех колпаках).[7]
- •Инверсия относительно окружности. Деление отрезка пополам с помощью одного циркуля. Стереографическая проекция.[7]
- •Полярное соответствие. Свойство взаимности поляр. Двойственность в геометрии. Теорема Паскаля. [7]
- •Векторы и комплексные числа.
- •Разное.
- •Литература по курсу элементарная математика (геометрия)
![]() Учебное
пособие
Учебное
пособие
Элементарная математика (дополнительные главы)
Исаев И.М.
Вопросы к экзамену по элементарной математике (4 курс, геометрия)
-
Замечательные точки в треугольнике .
Доказать, что медианы (биссектрисы, высоты, серединные перпендикуляры) пересекаются в одной точке. [7,8,9]
-
Доказать, что медианы треугольника делят площадь треугольника на 6 треугольников равной площади.
-
Доказать, что из медиан треугольника можно составить треугольник. Найти отношение площади этого треугольника к площади исходного треугольника.
-
Доказать, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины.
-
Найти множество точек равноудаленных от концов отрезка.
-
Найти множество точек равноудаленных от сторон угла.
-
Доказать, что вокруг любого треугольника можно описать окружность, причем только одну.
-
Доказать, что медианы (биссектрисы, высоты, серединные перпендикуляры) пересекаются в одной точке. Эти точки обозначаются буквами
 ,
соответственно, и называются центром
тяжести (центроидом), центром вписанной
окружности (инцентром), ортоцентром и
центром описанной окружности треугольника.
,
соответственно, и называются центром
тяжести (центроидом), центром вписанной
окружности (инцентром), ортоцентром и
центром описанной окружности треугольника. -
Доказать, что биссектриса треугольника делит противолежащую сторону в отношении равном отношению соответствующих боковых сторон. Это свойство называется основным свойством биссектрисы.
-
Доказать, что биссектриса внешнего угла треугольника делит противолежащую сторону в отношении равном отношению соответствующих боковых сторон. Это свойство называется основным свойством биссектрисы внешнего угла треугольника.
-
В треугольнике
 проведены биссектрисы внутренних углов
проведены биссектрисы внутренних углов
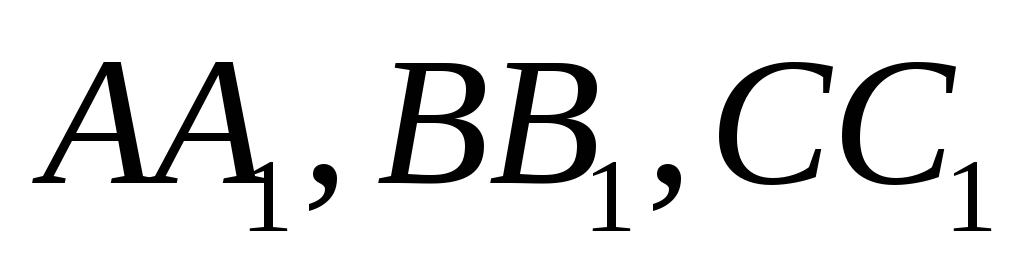 (
( - на сторонах треугольника). Известно,
что
- на сторонах треугольника). Известно,
что
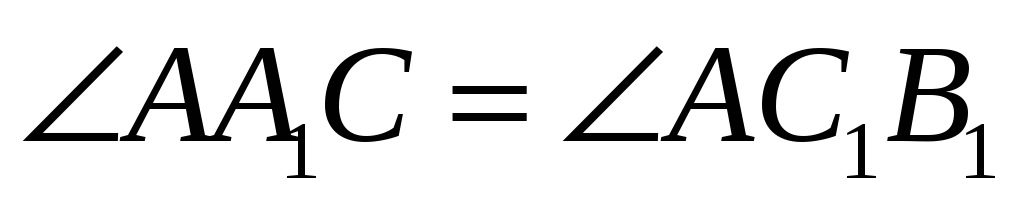 .
Найдите
.
Найдите
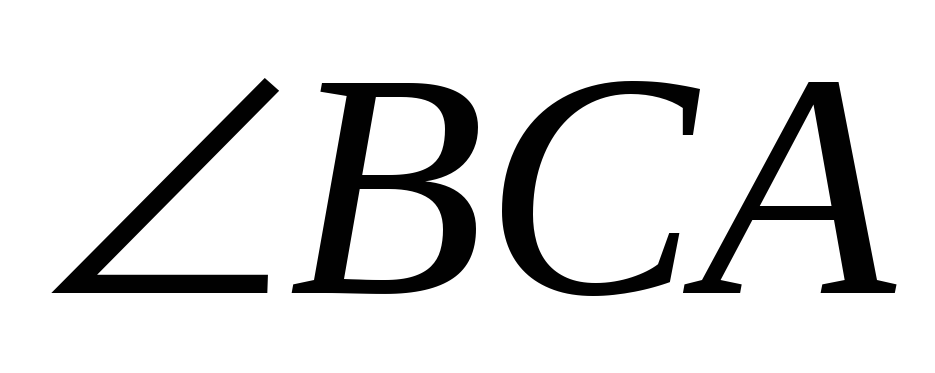 .
. -
Доказать, что для треугольника
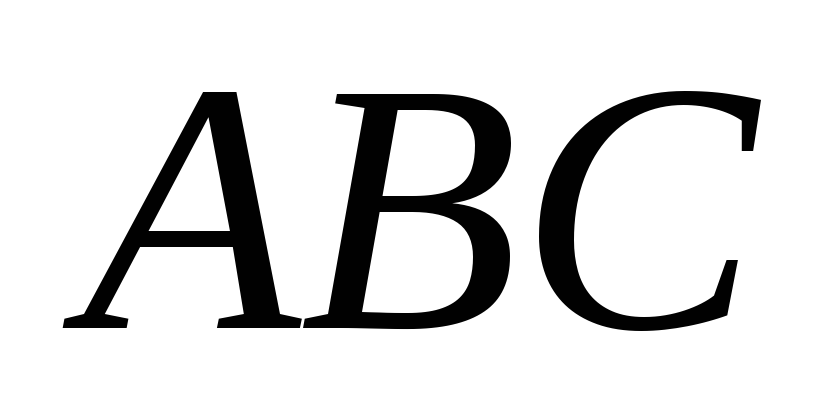 существуют четыре окружности, касающиеся
прямых
существуют четыре окружности, касающиеся
прямых
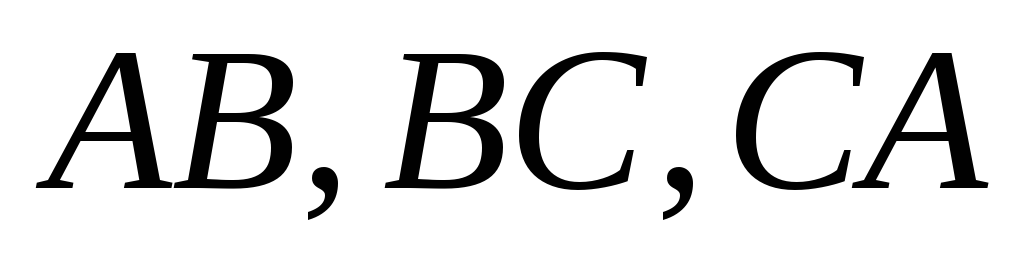 .
Что это за окружности? Где находятся
центры этих окружностей?
.
Что это за окружности? Где находятся
центры этих окружностей?
-
Средняя линия в треугольнике и ее свойства. Теорема Вариньона. Площади. [7,8,9].
-
Доказать, что средняя линия треугольника параллельна основанию и равна половине этого основания.
-
Доказать, что средние линии треугольника делят его на четыре равных треугольника.
-
Докажите, что средняя линия трапеции равна полусумме ее оснований.
-
Пусть
 -
медиана треугольника
-
медиана треугольника
 .
Докажите, что
.
Докажите, что
 .
. -
В четырехугольнике
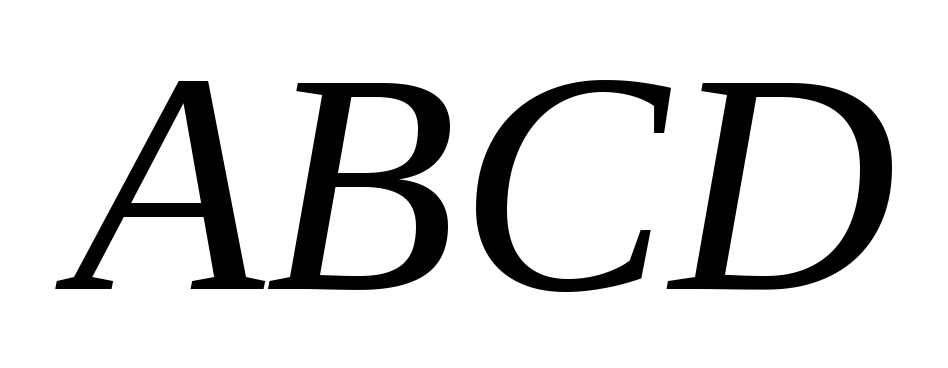 точка
точка
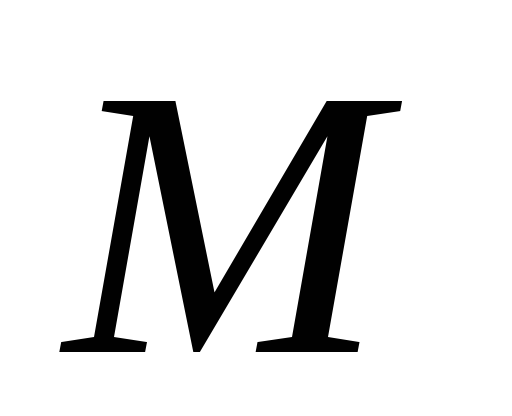 - середина стороны
- середина стороны
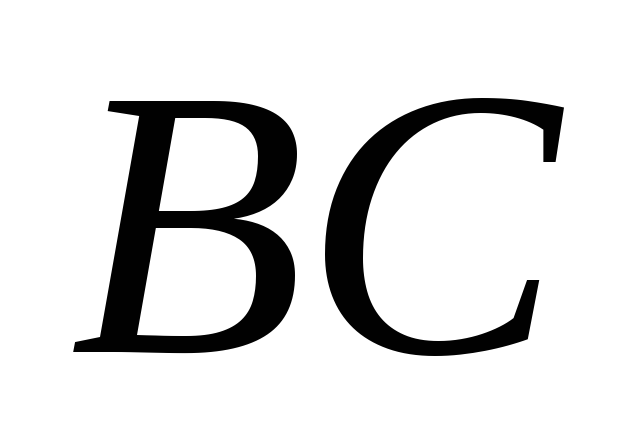 ,
точка
,
точка
 - середина стороны
- середина стороны
 .
Докажите, что
.
Докажите, что
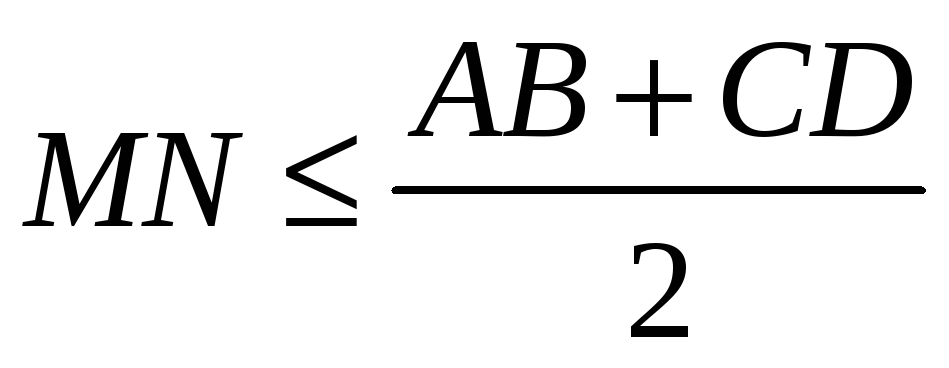 .
. -
Доказать, что четырехугольник, образованный последовательными серединами сторон данного четырехугольника, является параллелограммом. Найти отношение площади этого параллелограмма к площади исходного четырехугольника. Не забудьте рассмотреть случай невыпуклого четырехугольника.
-
Доказать, что средние линии четырехугольника точкой пересечения делятся пополам.
-
Докажите, что прямые, содержащие диагонали четырехугольника, взаимно перпендикулярны тогда и только тогда, когда отрезки соединяющие середины его противоположных сторон, равны.
-
Найдите площадь выпуклого четырехугольника
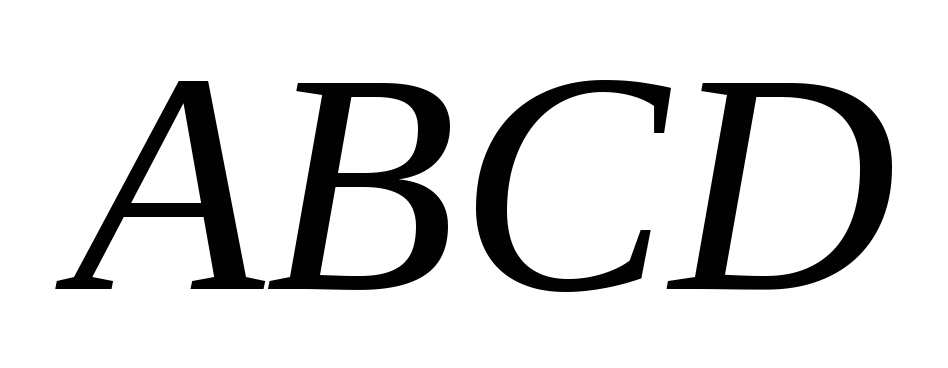 ,
если прямая
,
если прямая
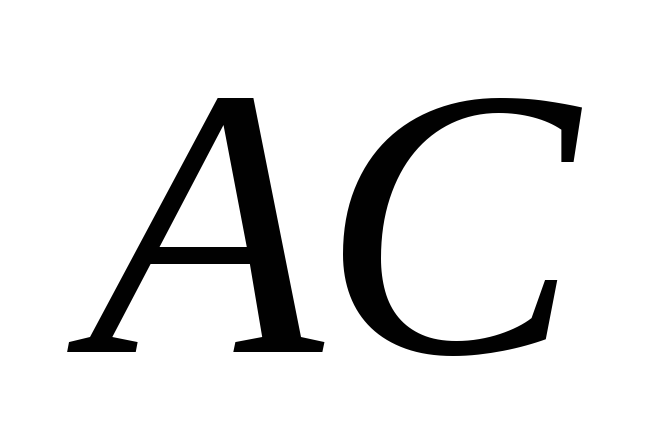 перпендикулярна
прямой
перпендикулярна
прямой
 и
и

-
Дан треугольник
 .
Точка
.
Точка
 лежит на продолжении стороны
лежит на продолжении стороны
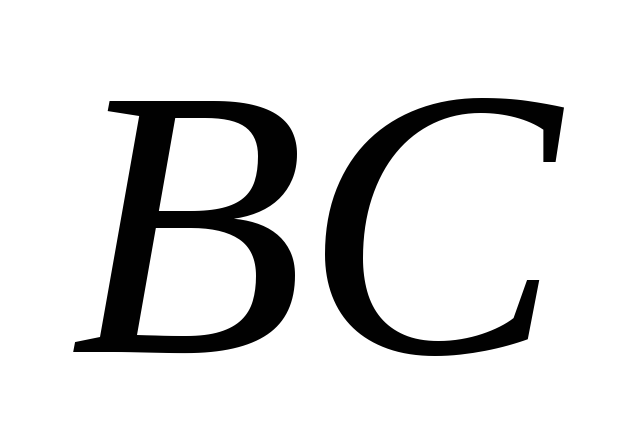 за точку
за точку
 ,
причем
,
причем
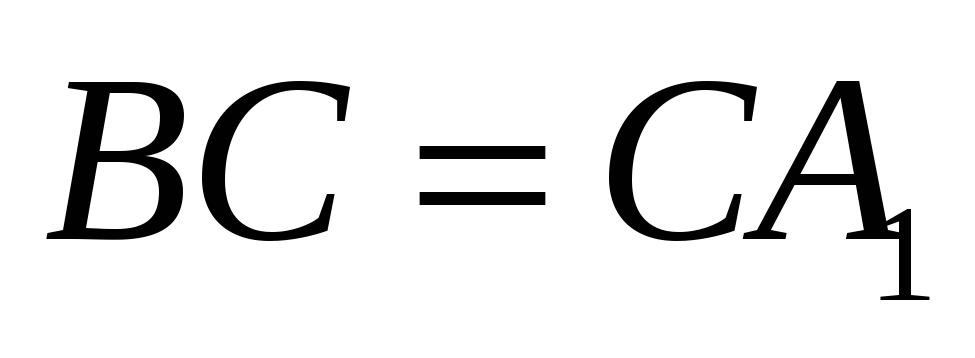 .
Аналогично строятся точки
.
Аналогично строятся точки
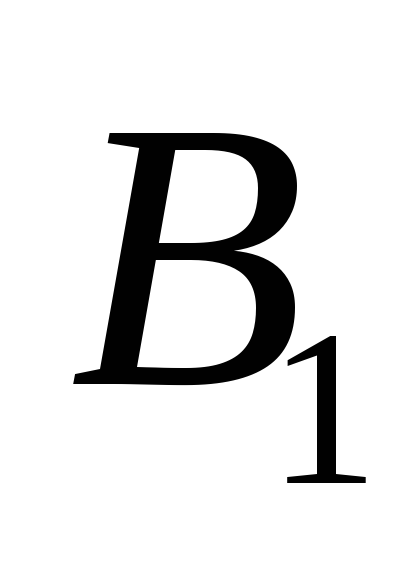 и
и
 .
Найти отношение площадей треугольников
.
Найти отношение площадей треугольников
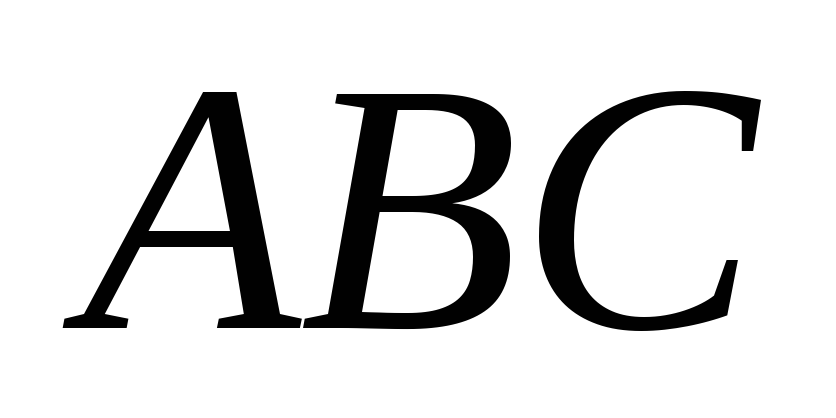 и
и
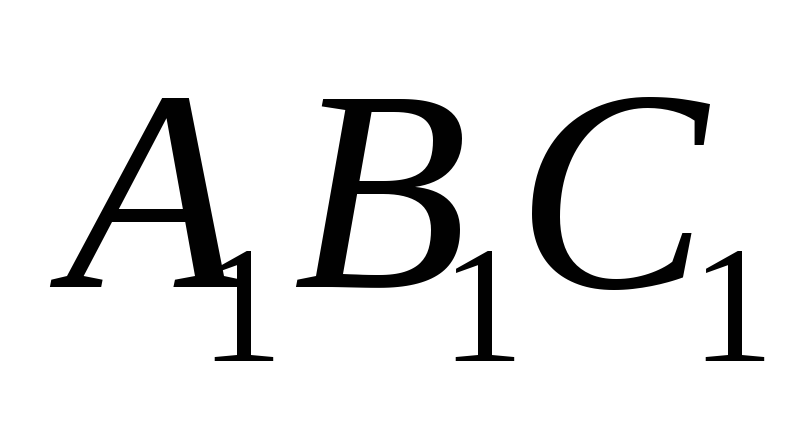 .
. -
Точка
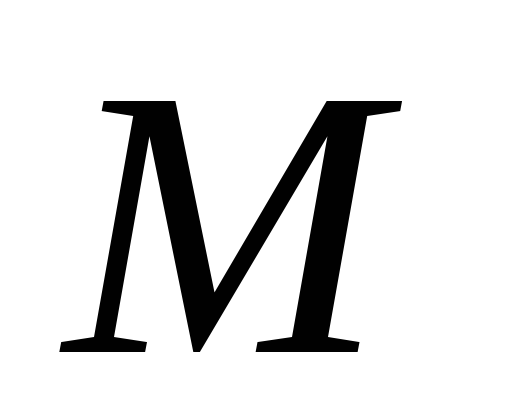 лежит внутри треугольника
лежит внутри треугольника
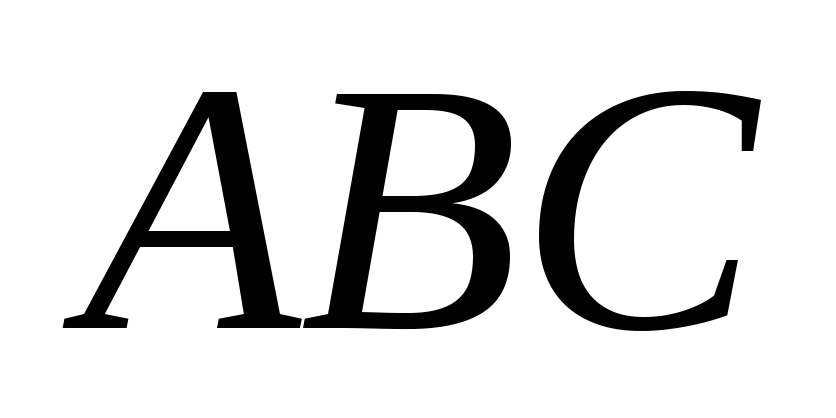 .
Докажите, что площади треугольников
.
Докажите, что площади треугольников
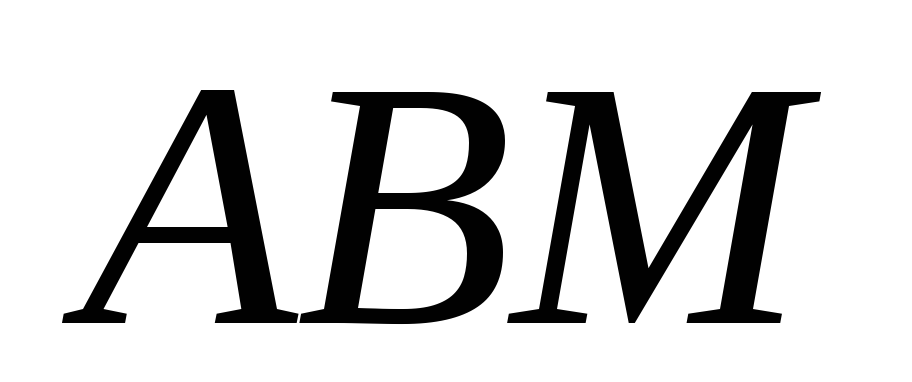 и
и
 равны тогда и только тогда, когда
равны тогда и только тогда, когда
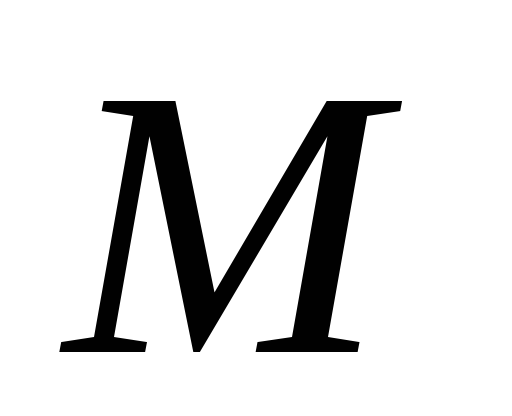 лежит на медиане
лежит на медиане
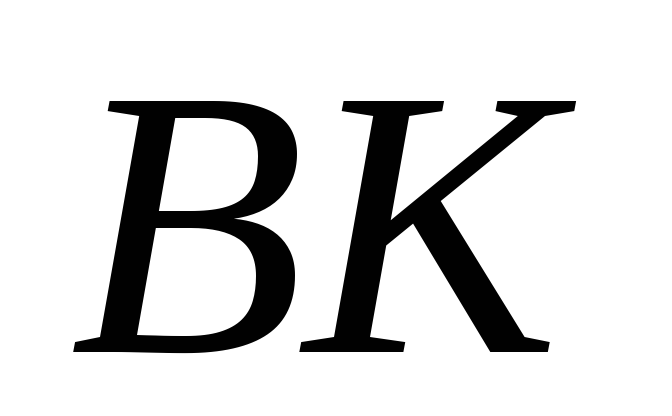 .
. -
Диагонали трапеции

 пересекаются в точке
пересекаются в точке
 .
Докажите, что площади треугольников
.
Докажите, что площади треугольников
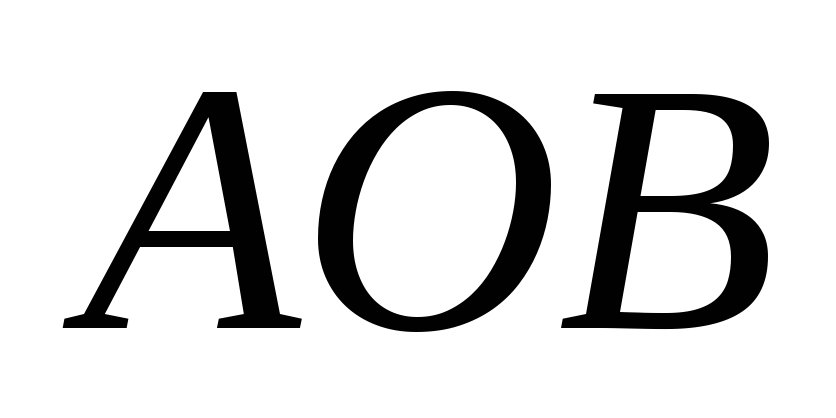 и
и
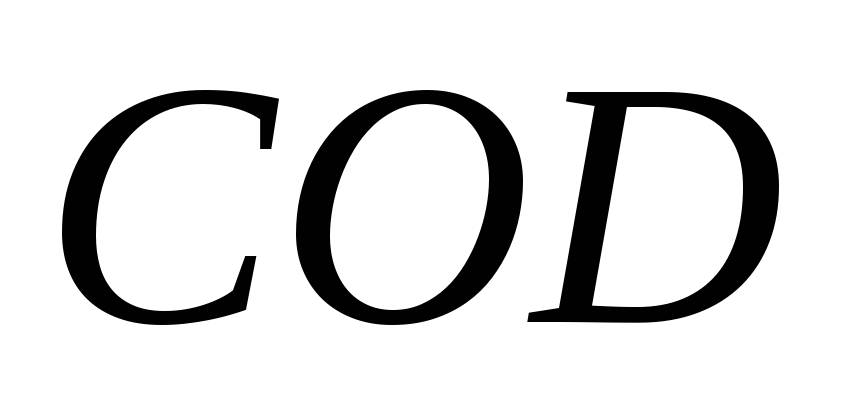 равны.
равны. -
В два противоположных угла четырехугольника
 вписываются два параллелограмма. Три
вершины каждого из этих параллелограммов
– середины смежных сторон и вершина
исходного четырехугольника
вписываются два параллелограмма. Три
вершины каждого из этих параллелограммов
– середины смежных сторон и вершина
исходного четырехугольника
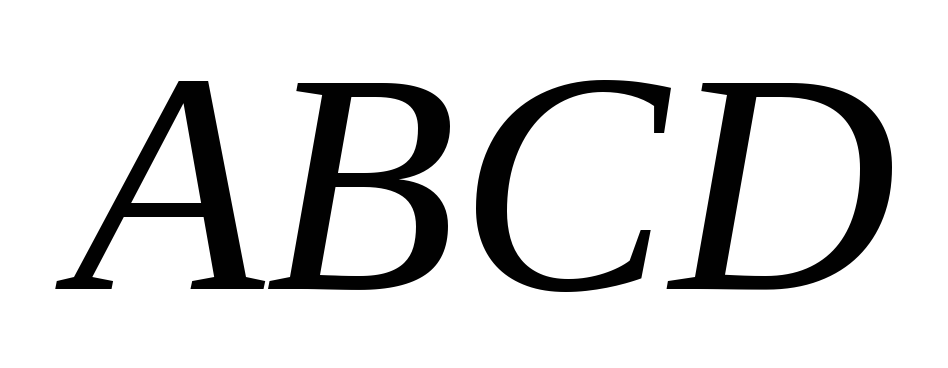 .
Доказать, что четвертая вершина этих
параллелограммов является общей.
.
Доказать, что четвертая вершина этих
параллелограммов является общей. -
Четырехугольник разрезан диагоналями на четыре треугольника. Докажите, что точки пересечения медиан этих треугольников образуют параллелограмм.
-
Четырехугольник
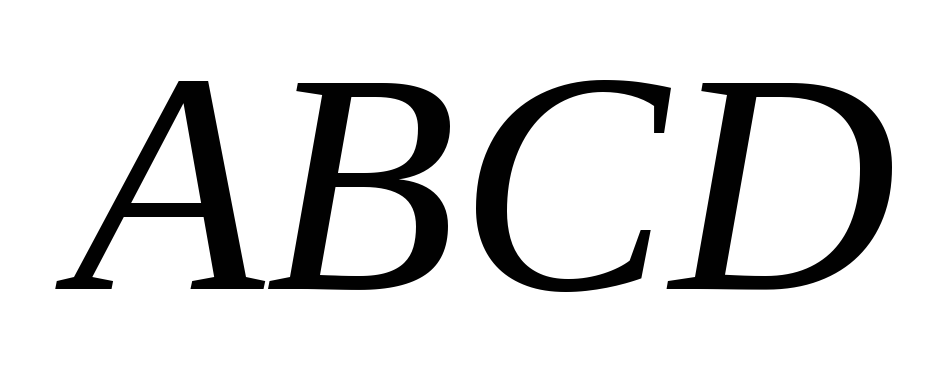 составлен из двух равнобедренных
прямоугольных треугольников
составлен из двух равнобедренных
прямоугольных треугольников
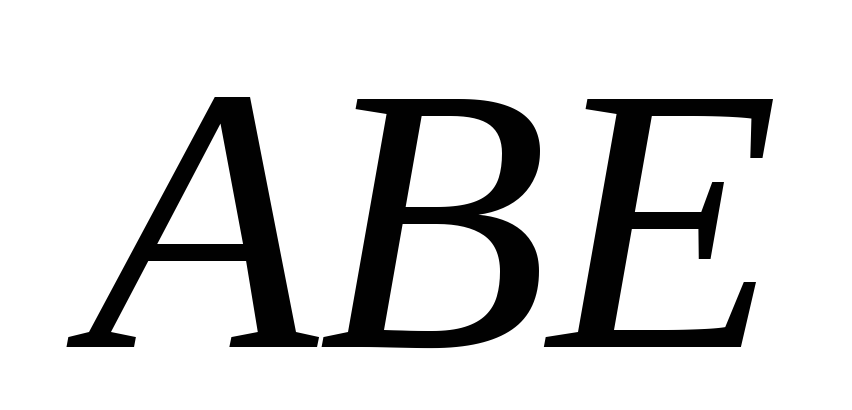 и
и
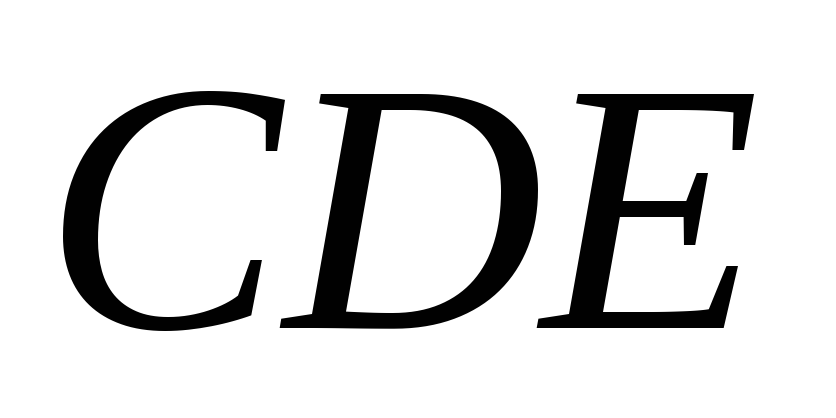 .
Пусть
.
Пусть
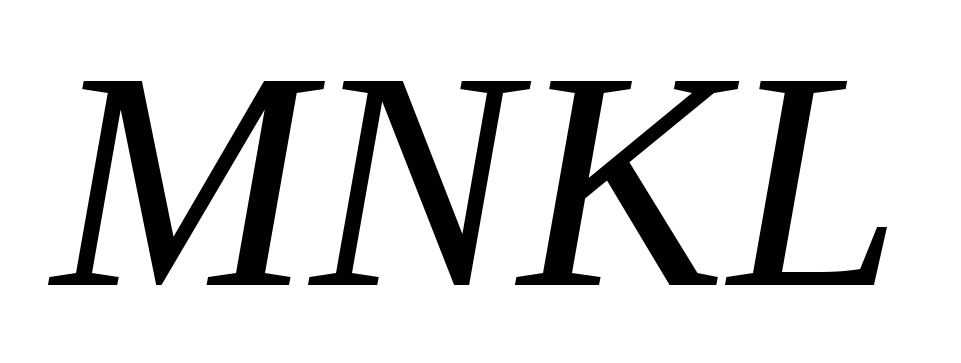 - четырехугольник, образованный
последовательными серединами сторон
- четырехугольник, образованный
последовательными серединами сторон
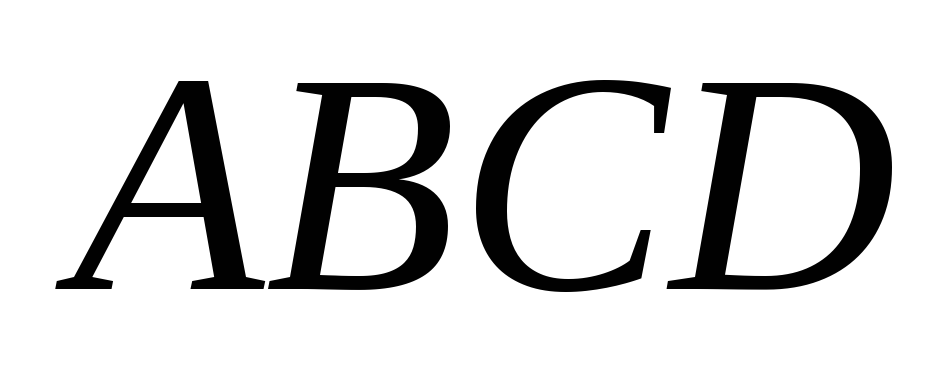 .
Доказать, что
.
Доказать, что
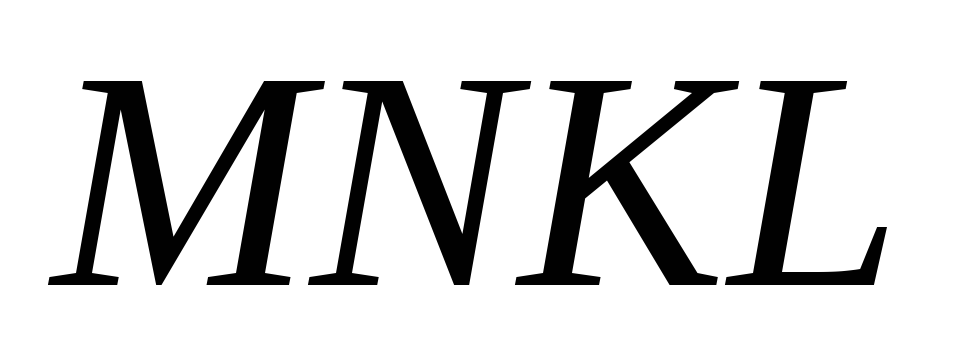 - квадрат.
- квадрат.
