Шпоры / Шпоры(МП-23_edition) / 05

5. Обратная решетка. В идеальном кристалле определенные структурные единицы (ато­мы, группы атомов, молекулы, ионы) периодически повторяются в про­странстве. Положение каждой структурной единицы задается математи­ческой точкой, называемой узлом. Система периодически повторяю­щихся узлов образует пространственную решетку.

При анализе пространственных решеток кристаллов используется фундаментальное понятие решетки Браве. По определению трехмерная решетка Браве является множеством точек, образованных концами век­торов вида: , где , , - три некомпланарных вектора; , , - все возможные целые числа.

Любой из векторов называется вектором трансляции решетки, а векторы , , - основными векторами трансляции.

Смещение решетки в направлении вектора на расстояние l при­водит к ее самосовмещению. Это основное свойство любой пространст­венной решетки называется трансляционной симметрией. Однако кри­сталлы и их решетки могут обладать и другими элементами симметрии: осями симметрии, плоскостями симметрии, центром инверсии. В кри­сталлографии показывается, что всего существует 14 различных реше­ток Браве, каждая из которых определяется своим набором элементов

симметрии.

Пространственная решетка является математической абстракцией.

В реальном кристалле около каждого узла расположена группа атомов, называемая базисом. Пространственная решетка вместе с базисом обра­зуют кристаллическую структуру.

Разные кристаллы могут иметь одинаковые решетки. Так, кристаллы германия, кремния и арсенида галлия обладают гранецентрированной ку­бической решеткой Браве, в то время как германий и кремний имеют структуру алмаза, а арсенид галлия - структуру цинковой обманки.

Параллелепипед, построенный на основных векторах трансляции, называется элементарной ячейкой решетки. Элементарная ячейка лю­бой решетки Браве является примитивной или простой, на нее приходится один узел решетки. Объем элементарной ячейки определяется смешанным произведением основных векторов трансляции: .

Выбор основных векторов трансляции неоднозначен, поэтому не­однозначен и выбор элементарной ячейки, построенной на этих векто­рах. Однако существует элементарная ячейка, которая для заданной ре­шетки оказывается единственной. Это так называемая ячейка Вигнера -Зейтца.

Построим ее следующим образом (рис.2. 1). Примем за центр ячейки какой-либо узел решетки. Выбранный узел соединим с ближайшими узлами прямыми линиями и через середины образовавшихся отрезков проведем перпендикулярные плоскости. Тело, образованное плоскостя­ми вокруг центра ячейки, и является элементарной ячейкой Вигнера-Зейтца. Очевидно, что элементарная ячейка Вигнера - Зейтца простая, и ее трансляцией можно построить весь кристалл. При этом любая точка ячейки распо­ложена ближе к ее центру, чем к любому другому узлу решетки. Объем ячейки Вигнера – Зейтца равен объему элементарной ячей­ки решетки Браве.

Н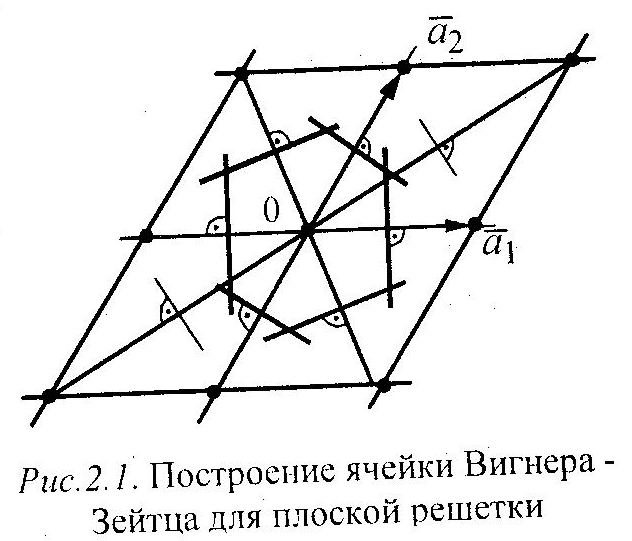айдем для основных векто­ров трансляции , , такие три вектора , , , которые обладают следующим свойством: скалярное произведение вектора на вектор (i, j = 1,2,3) равно 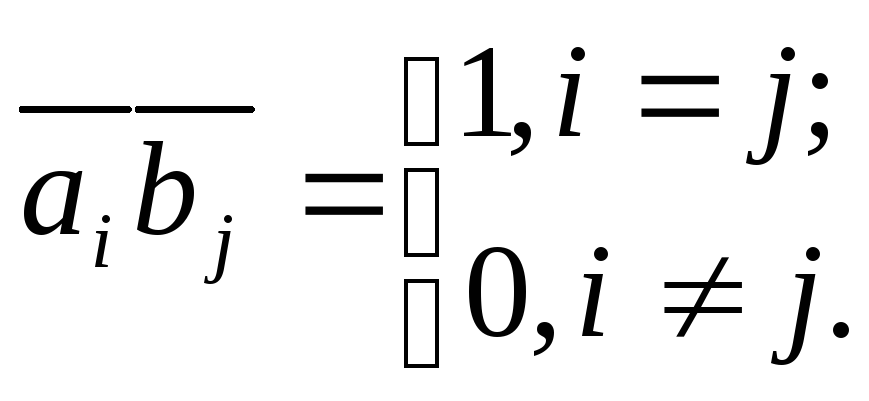Таким свойством обладают векторы: , , .

Очевидно что размерность векторов , , - обратная длина, т.е. эти векторы заданы в так называемом обратном пространстве.

Решетка, построенная на векторах , , называется обратной решеткой кристалла. Произвольный вектор трансляции обратной решетки имеет вид , где , , - целые числа.

Для кубического кристалла ===, и векторы , , взаимно перпендикулярны. Поэтому для кубического кристалла обрат­ная решетка является тоже кубической, причем .

Можно показать, что для объемно-центрированной решетки обрат­ной является гранецентрированная, для гранецентрированной - объем­но-центрированная. В частности, объемно-центрированную обратную решетку имеют кристаллы германия, кремния и арсенида галлия.

Обратное пространство и обратная решетка не являются отвлечен­ными абстрактными понятиями, они имеют вполне реальное физиче­ское содержание и играют фундаментальную роль при анализе волно­вых процессов в кристаллах. Дело в том, что волновые векторы любых волн (электронных, упругих, электромагнитных), распространяющихся в кристаллах, задаются в обратном пространстве. При этом каждому вектору обратной решетки соответствует волна с периодом, равным некоторому вектору трансляции прямой решетки.

2. Зоны Бриллюэна. Хотя вектор имеет смысл волнового вектора, он отличается от волнового вектора свободного электрона тем, что в кристалле вектор определяется неоднозначно. Можно показать, что если взять два вектора и ’, отличающиеся друг от друга на величину вектора обратной решетки ’=+, то , т.е. векторы и + описывают одинаковые квантовые состояния электрона. Поэтому вектор правильнее называть квазиволновым вектором, а величину - квазиимпульсом.

Поскольку векторы и + описывают одинаковые квантовые состояния, то и энергия в этих состояниях одна и та же: .

Другими словами, энергия электрона является периодической функцией в пространстве обратной решетки.

В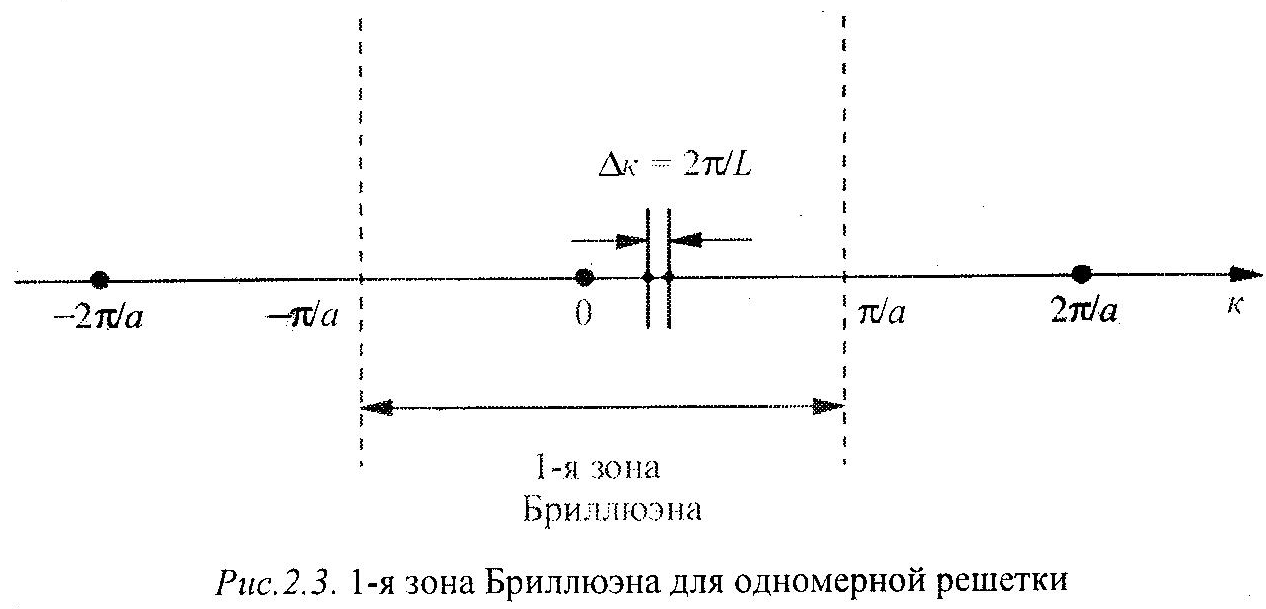 силу периодичности для определения спектра энергии электрона в кристалле, т.е. разрешенных значений энергии Е, нет необ­ходимости рассматривать все -пространство, достаточно ограничить­ся одним периодом функции , т.е. одной элементарной ячейкой об­ратной решетки.

Разумно выбрать элементарную ячейку так, чтобы величины всех физически различных значений были минимальными. Очевидно, что лучше всего этому удовлетворяет ячейка Вигнера - Зейтца.

Элементарная ячейка Вигнера - Зейтца обратной решетки, постро­енная около начала координат, называется 1-й зоной Бриллюэна.

Для одномерной решетки с параметром а обратная решетка одно­мерна и строится на векторах (рис.2.3). Число физически различных значений к в 1-й зоне Бриллюэна, а вместе с ними и число раз­решенных уровней энергии электрона в кристалле можно найти, разделив объем зоны Бриллюэна на объем, приходящийся на один вол­новой вектор , равный .

Для простой кубической решетки объем 1-й зоны Бриллюэна равен , где - объем элементарной ячейки прямой решетки.

Число разрешенных уровней энергии, таким образом, равно .

Если на элементарную ячейку приходится один атом, то - числу атомов в кристалле. В то же время число разре­шенных состояний с учетом спина в два раза больше - 2N.

Полученный вывод сделан для простой кубической решетки. Мож­но показать, что он остается справедливым и для других решеток.