Шпоры / Шпоры(МП-23_edition) / 07

7. Квазичастицы в полупроводниках.

Квазичастицы хар-ся квазиимпульсом и квазиволновым вектором.

Закон дисперсии

Закон дисперсии - зависимость энергии от квазиимпульса в разрешенной зоне. Закон дисперсии удобно изображать графически. Обычно пользуются одним из двух представлений.

Во-первых, можно фиксировать две из трех компонент квазиимпульса. Пусть, например, фиксированы компоненты и . Тогда зависимость определяет некоторую кривую на плоскости (,). Кривые такого типа называются дисперсионными. Совокупность их, соответствующая различным значениям и , полностью характеризует закон дисперсии.

Во-вторых, можно фиксировать значение энергии в l-той зоне, полагая, что (6.1). Уравнение (6.1) определяет поверхность в трехмерном пространстве квазиимпульсов. Ее называют изоэнергетической (или поверхностью равных энергий). Придавая различные значения константе, стоящей в правой части (6.1), и задавая форму соответствующей изоэнергетической поверхности, мы полностью описываем закон дисперсии.

Понятие дырки

Рассмотрим полностью заполненную валентную зону полупровод­ника, содержащую М электронов. Электроны полностью заполненной зоны не могут участвовать в электропроводно­сти, ток, создаваемый ими, равен нулю (почему?): , где - ток, создаваемый j-м электроном.

Пусть под действием термической ионизации один электрон пере­шел из валентной зоны в зону проводимости (рис. 2. 13, а). Ток, создавае­мый оставшимися М-1 электронами, равен .

Таким образом, ток, создаваемый электронами полностью заполненный зоны, из которой удален один электрон, равен по величине и противоположен по направлению току, создаваемому одним удаленным

Электроном, но точно такой же ток создает частица с положительным зарядом и положительной эффективной массой, помещенная на незанятое место удаленного электрона (рис.2.13,б). Такая частица, точнее квазичастица, называется дыркой. Если удаленный электрон обладает зарядом е, эффективной массой , квазиимпульсом , скоростью , спином , то дырке необходимо приписать следующие свойства: , , , , .

В состоянии термодинамического равновесия электроны стремятся занять самые низкие энергетические состояния. Если незанятое состояние находится в глубине валентной зоны, то электроны с более высших уровней стремятся занять это состояние. В результате незаполненное состояние – дырка поднимается к потолку валентной зоны подобно пузырьку воздуха в воде. Это означает, что направления отсчета энергии дырок и электронов противоположны друг другу: .

Наименьшей энергией обладают дырки вблизи потолка валентной зоны. Для них справедливо введенное ранее представление об эффективной массе, а их движение можно описать уравнениями, подобными уравнениям (2.13) - (2.15) для электрона.

Таким образом, с точки зрения зонной теории дырочная проводимость полупроводника обусловлена электронами почти заполненной валентной зоны, а концентрация дырок р определяется числом свободных состояний в этой зоне.

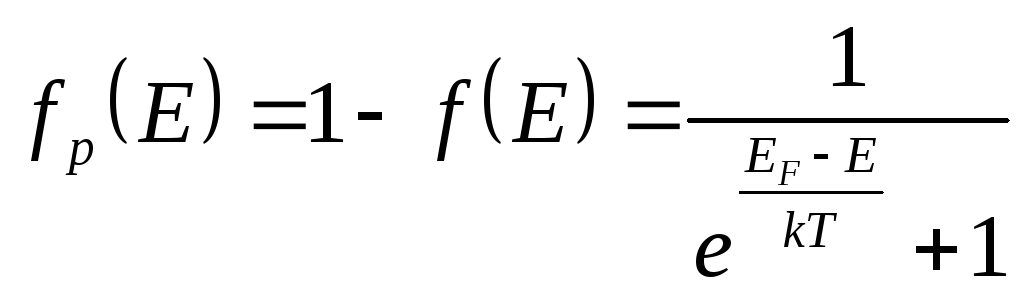В то же время с точки зрения статистики дырку можно определить как незанятое электроном состояние на энергетическом уровне Е, поскольку дырка помещается на место удаленного электрона. Поэтому вероятность заполнения энергетического уровня Е дыркой будет равна вероятности отсутствия на этом уровне электрона: , где функция распределения Ферми - Дирака.

Подобно электронам зоны проводимости, образующим электрон­ный газ, дырки валентной зоны образуют дырочный газ, который может быть вырожденным или невырожденным. При этом полный ток в полупроводнике складывается из токов, создаваемых электронами зоны про­водимости и дырками валентной зоны.

Квазиимпульс

Состояние электрона, свободно движущегося в пространстве, как известно, можно охарактеризовать энергией Е и импульсом Р. При этом связь между энергией и импульсом дается формулой .

Согласно де Бройлю свободному электрону массы , движущемуся со скоростью v, соответствует волна, длина которой может быть определена из соотношения , где h — постоянная Планка.

Так как волновое число — число волн, укладывающихся на длине см, равно: , то импульс свободного электрона , а его энергия , где - квант действия.

Для электрона, движущегося в периодическом поле кристалла, можно ввести величину , называемую квазиимпульсом. В соответствии с дискретным спектром k (;;, =0,,,…; =0,,,…; =0,,,…, где , , - размеры кристалла в форме параллелепипеда) квазиимпульс р также должен принимать ряд дискретных значений. Т.к. компоненты вектора k - ,, - находятся в интервалах от до , то в кубической решетке квазиимпульс должен изменяться в пределах , i=x,y,z.

Энергия электрона в кристалле – четная функция квазиимпульса, т.е. .

Эффективная масса

Уравнение Шредингера для электрона в кристалле (2.1): отличается от уравнения Шредингера для свободного электрона (1.3): наличием периодического потенциала решетки .

Предположим, что вместо уравнения (2.1) можно записать эквива­лентное ему уравнение: (2.7), в котором отсутствует периодический потенциал решетки, а его влия­ние учитывается путем введения некоторой неизвестной величины , имеющей размерность массы.

Закон дисперсии, получаемый из решения уравнения (2.7), имеет вид, аналогичный закону дисперсии для свободного электрона (1.5):

т.е. энергия квадратично зависит от вектора .

В то же время, как было рассмотрено выше, зависимость , получаемая из решения уравнения (2.1), является некоторой периодиче­ской функцией вектора . Таким образом, уравнение (2.1) можно пред­ставить в виде (2.7) только для тех областей спектра электрона, где его энергия квадратично зависит от квазиволнового вектора . Рассмотрим на примере одномерного кристалла, когда это имеет место.

Закон дисперсии для электрона в одномерном кристалле представляет собой периодическую функцию, имеющую экстремумы вблизи потолка и дна разрешенной зоны. В силу симметрии зоны Бриллюэна в центре ее всегда имеется экстремум энергии. Разложим функцию в ряд Тейлора вблизи точки k = 0 и ограничимся квадратичным членом разложения: . По определению экстремума . Принимая за начало отсчета энергии величину , получаем (2.9).

Сравнивая выражения (2.8) и (2.9), можно видеть, что они совпадают, если в качестве взять величину (2.10).

Величина называется эффективной массой электрона.

Таким образом, уравнение (2.7) оказывается справедливым для электронов, находящихся вблизи экстремумов энергии, т.е. вблизи дна и потолка разрешенной зоны. Движение таких электронов в кристалле можно рассматривать как движение свободных электронов, если припи­сать электрону массу , отличную от массы свободного электрона т.