
Шпоры / Шпоры(МП-23_edition) / 04
.doc
4.
Уравнение Шредингера для электрона
в кристалле (2.1):
![]() отличается
от уравнения Шредингера для свободного
электрона (1.3):
отличается
от уравнения Шредингера для свободного
электрона (1.3):
![]() наличием
периодического потенциала решетки U(r)
наличием
периодического потенциала решетки U(r)
Предположим,
что вместо уравнения (2.1) можно записать
эквивалентное ему уравнение:
![]() (2.7), в котором отсутствует периодический
потенциал решетки, а его влияние
учитывается путем введения некоторой
неизвестной величины m*n
,имеющей размерность массы.
(2.7), в котором отсутствует периодический
потенциал решетки, а его влияние
учитывается путем введения некоторой
неизвестной величины m*n
,имеющей размерность массы.
Закон
дисперсии, получаемый из решения
уравнения (2.7), имеет вид, аналогичный
закону дисперсии для свободного электрона
(1.5): E(![]() )=
)=
![]() (2.8) т.е. энергия квадратично зависит
от вектора
(2.8) т.е. энергия квадратично зависит
от вектора
![]() .
.
В
то же время, как было рассмотрено выше,
зависимость Е(![]() )
, получаемая из решения уравнения
(2.1), является некоторой периодической
функцией вектора
)
, получаемая из решения уравнения
(2.1), является некоторой периодической
функцией вектора
![]() .
Таким образом, уравнение (2.1) можно
представить в виде (2.7) только для тех
областей спектра электрона, где его
энергия квадратично зависит от
квазиволнового вектора
.
Таким образом, уравнение (2.1) можно
представить в виде (2.7) только для тех
областей спектра электрона, где его
энергия квадратично зависит от
квазиволнового вектора
![]() .
Рассмотрим на примере одномерного
кристалла, когда это имеет место.
.
Рассмотрим на примере одномерного
кристалла, когда это имеет место.
Закон
дисперсии для электрона в одномерном
кристалле представляет собой
периодическую функцию, имеющую экстремумы
вблизи потолка и дна разрешенной
зоны. В силу симметрии зоны Бриллюэна
в центре ее всегда имеется экстремум
энергии. Разложим функцию Е(k)
в ряд Тейлора вблизи точки к = 0 и
ограничимся квадратичным членом
разложения: E(k)=E(0)+![]()
![]() .
.
По
определению экстремума
![]() =
0. Принимая за начало отсчета энергии
величину Е(0), получаем E(k)=
=
0. Принимая за начало отсчета энергии
величину Е(0), получаем E(k)=![]() (2.9)
(2.9)
Сравнивая выражения (2.8) и (2.9), можно видеть, что они совпадают, если в качестве m*n взять величину
![]() (2.10)
Величина m*n
называется эффективной
массой электрона.
(2.10)
Величина m*n
называется эффективной
массой электрона.
Таким образом, уравнение (2.7) оказывается справедливым для электронов, находящихся вблизи экстремумов энергии, т.е. вблизи дна и потолка разрешенной зоны. Движение таких электронов в кристалле можно рассматривать как движение свободных электронов, если приписать электрону массу m*n, отличную от массы свободного электрона m.
Рассмотрим
трехмерный случай, полагая при этом,
что экстремум энергии находится в
некоторой точке
![]() 0
зоны Бриллюэна. Разлагая функцию Е(
0
зоны Бриллюэна. Разлагая функцию Е(![]() )
в ряд и ограничиваясь квадратичными
членами разложения, получаем
)
в ряд и ограничиваясь квадратичными
членами разложения, получаем
E(![]() )=E(
)=E(![]()
![]() )+
)+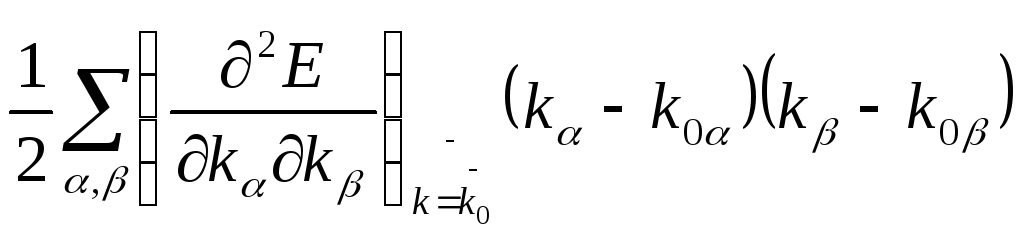 =E(
=E(![]() 0)+
0)+![]()
(2.11)
где а,b
независимо могут принимать значения
х, у, z,
а выражение
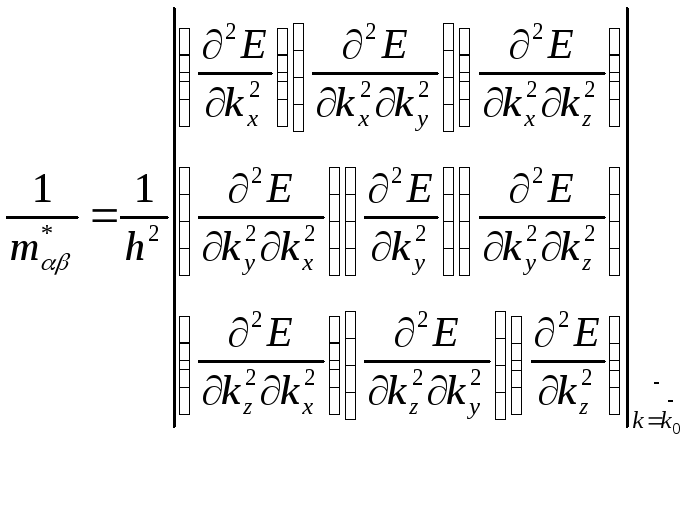 =
=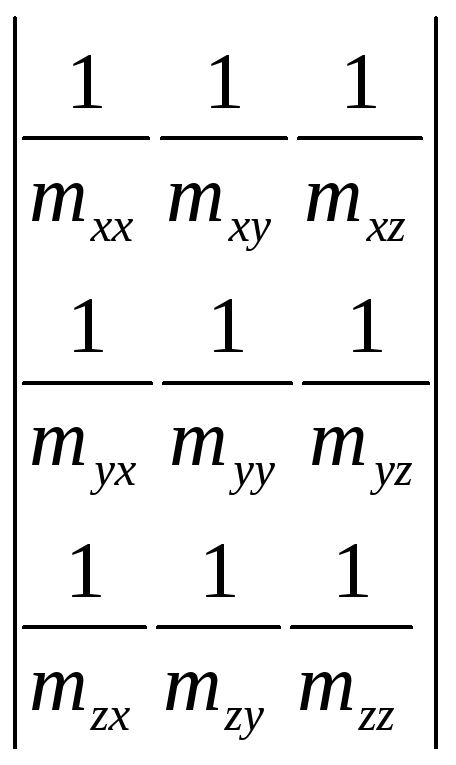
определяет тензор обратной эффективной массы. Поскольку велична второй производной не зависит от порядка дифференцирования, тензор симметричен: mab = mba. Симметричный тензор в главных осях
приводится к диагональному
виду, при котором все члены, не стоящие
на главной диагонали, обращаются в нуль:
![]() =
= =
=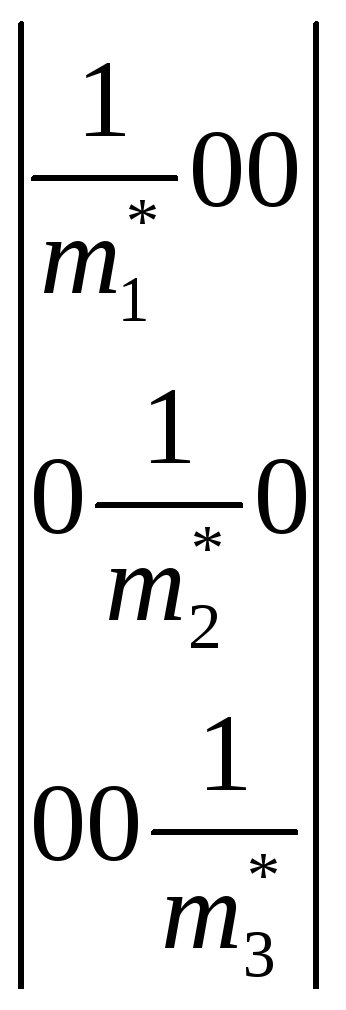
Таким
образом, и в общем случае вблизи точки
экстремума энергия квадратично зависит
от квазиволнового вектора, и электрону
можно приписать эффективную массу.
Однако в отличие от одномерного в общем
случае эффективная масса зависит от
направления движения электрона и
характеризуется тремя компонентами
тензора эффективной массы: m![]() ,
m
,
m![]() , m
, m![]() Используя диагональный вид тензора
обратной Эффективной массы, разложение
(2. 11) можно записать в виде
Используя диагональный вид тензора
обратной Эффективной массы, разложение
(2. 11) можно записать в виде
E(![]() )-E(
)-E(![]() )=
)=
Для
Е(![]() )=const
это есть уравнение изоэнергетической
поверхности, которая представляет собой
эллипсоид, полуоси которого определяются
компонентами тензора эффективной массы.
)=const
это есть уравнение изоэнергетической
поверхности, которая представляет собой
эллипсоид, полуоси которого определяются
компонентами тензора эффективной массы.
Для
многих кристаллов, например, для германия
и кремния,
![]() =
=![]() =
=![]() ,
,
![]() =
=
![]() и изоэнергетическая
поверхность представляет собой эллипсоид
вращения вокруг оси кz
:
и изоэнергетическая
поверхность представляет собой эллипсоид
вращения вокруг оси кz
:
E(![]() )-E(
)-E(![]() )=
)=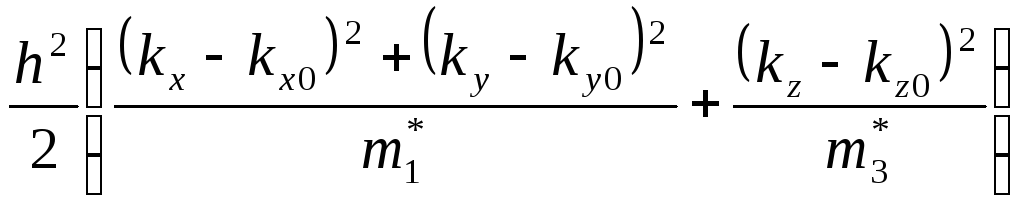 .
Компоненты
.
Компоненты
![]() и
и
![]() называют в этом
случае поперечной и продольной
эффективными массами.
называют в этом
случае поперечной и продольной
эффективными массами.
