Метод Коши

Пусть дана неоднородная система ЛДУ: (1)

Нормальная фундаментальная система решений, соответствующая системе (1) известна:

(2)

И известна нормальная фундаментальная система решений системы (3):

(3)

Система (3) называется сопряженной к системе (2).

Пусть - нормальная фундаментальная система решений (2); - нормальная фундаментальная система решений (3).

Начальные условия - . Скалярное произведение . Покажем, что во всех точках отрезка , скалярное произведение равно , то есть

(4)

Покажем, что , .

Построим решение нашего Дифференциального Уравнения методом Коши. Будем его искать в виде: , (5)

где - неизвестные скалярные функции. Подставим (5) в (1):

, . (6)

Так как функции - решение однородной системы ДУ (1).

Умножим (6) скалярно на : , ,

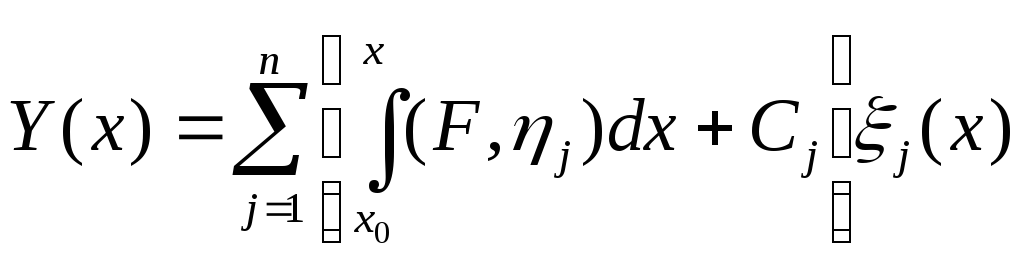. (7)

Метод Коши применяется, когда мы можем построить две взаимно ортогональных системы нормальных фундаментальных решений.

Системы линейных дифференциальных уравнений с

постоянными коэффициентами

, (1)

где - матрица с постоянными коэффициентами.

(2)

неоднородная система ДУ.

Решение (1) будем искать в виде , (3)

где - вектор, .

Подставив решение в (1), получим: - -собственные значения, - собственные векторы.

1. Все корни характеристического уравнения действительны и различны. Это значит, - - частные решения однородной системы.

следовательно, общее решение однородной системы имеет следующий вид: (4)

Воспользуемся основной теоремой алгебры о представлении вещественной матрицы:

Проинтегрировав систему покомпонентно, получаем: . Тогда общее решение однородной системы ДУ , где матрица состоит из собственных векторов матрицы А.

2. Характеристическое уравнение имеет комплексный корень .

Если матрица вещественная, то будет существовать комплексно сопряженный корень характеристического уравнения. Общее решение (1) может быть представлено в виде (4).

Согласно следующей теореме:

Теорема. Если оператор - вещественный, а -функции принимающие действительные значения, а -решение однородного уравнения , тогда будут тоже действительными решениями .

То есть, если вещественная матрица, то паре комплексно сопряженных корней характеристического уравнения будет соответствовать пара действительных решений, а именно: .

3. Корень характеристического уравнения имеет кратность .

В этом случае для матрицы строится Жорданова Нормальная Форма и общее решение СЛДУ имеет вид: , постоянные векторы. Максимальная степень полинома соответствует максимальной степени элементарного делителя для характеристического числа .

, -соответствующая Жорданова Нормальная Форма. Допустим, что у нас есть одна клетка Жордана размерности , соответствующая собственному числу :

.

Тогда покомпонентно система будет иметь вид:

Начнем интегрировать эту систему с -го уравнения:

.

Затем решим -ое уравнение методом вариации постоянных, используя уже известное решение .

.

Продолжая процесс интегрирования получим все компоненты вектора .

Общее решение однородной системы ДУ имеет вид: , где матрица Р состоит из собственных и присоединенных векторов матрицы А, соответствующих собственному числу .

Матричные дифференциальные уравнения.

Пусть дано матричное дифференциальное уравнение: , (1)

где (2)

с начальными значениями: . (3)

Теорема. Если матрица непрерывна на , а определитель матрицы , то на существует единственное решение уравнения (1) и определитель Вронского этого решения не обращается в ноль ни в одной точке .

Будем рассматривать одновременно с системой (1) систему вида:

(4)

Уравнение (4) называется сопряженным для уравнения (1).

Теорема. Пусть - решение (1), а матрица непрерывна на , тогда - существует на и является решением системы (4).

Доказательство: По предположению теоремы решение на существует и определитель этого решения не равен нулю в любой точке , следовательно, существует обратная матрица . А так как , то продифференцировав это соотношение, получаем: ,

где - решение уравнения (1), следовательно, 

Рассмотрим систему - линейно независимых неоднородных дифференциальных уравнений

. (5)

Будем искать решение этой системы методом вариации постоянной.

Обозначим - решение (1). Будем искать решение системы (5) в виде:

, (6)

где - неизвестная вектор-функция.

Подставим (6) в (5):

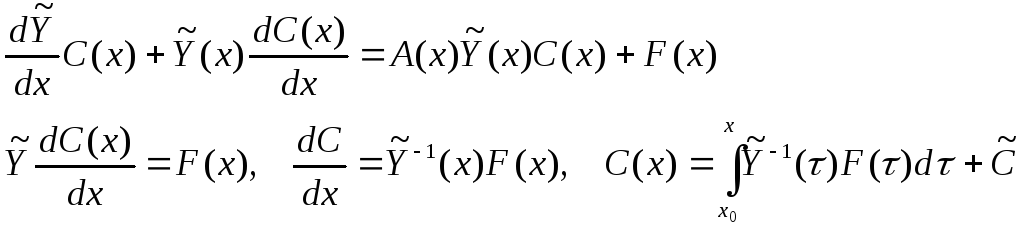
Тогда общее решение неоднородной системы будет иметь вид:

(7)

Теорема. Общее решение неоднородной системы (5) можно представить в виде: , (8)

где - общее решение соответствующей однородной системы.

Замечание. Пусть матрица постоянна и начальные условия имеют вид: (9)

Покажем, что решение уравнения (9) - удовлетворяет функциональному уравнению:

. (10)

При любом фиксированном матрицы и будут решением (9). При эти матрицы будут совпадать в силу начальных условий и, следовательно, по теореме о существовании и единственности они будут совпадать для любых . Если воспользоваться (10), то можно записать (сделав замену , и умножив соотношение (10) справа на ):

. (11)

Сравнив (11) и (7), сделаем вывод о том, что общее решение неоднородной системы ДУ с постоянной матрицей А может быть представлено в виде:

. (12)