!Механика и электродинамика / Лабораторные работы / LAB8

7

Л а б о р а т о р н а я р а б о т а № 8.

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ И ПРОВЕРКА ТЕОРЕМЫ ШТЕЙНЕРА.

Цель работы: экспериментальное определение момента инерции твердого тела с помощью трифилярного подвеса и проверка теоремы Штейнера.

Оборудование: установка, миллиметровая линейка, секундомер.

Продолжительность: 4ч.

Описание установки. Теоретическая часть.

Момент инерции это величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением:

,

где  m_i –элементарные массы тела, r_i – их расстояния от оси вращения.

Момент инерции тела относительно какой-либо оси можно найти вычислением или измерить экспериментально. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла:

, (1)

где dm и dV – масса и объем элемента тела, находящегося на расстоянии r от интересующей нас оси,  – плотность тела. Интегрирование должно производиться по всему объему тела.

Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы. Например, для цилиндра или диска можно получить следующую формулу для нахождения величины момента инерции относительно оси симметрии:

, (2)

где т – масса, R₀ - радиус цилиндра или диска.

Для тел неправильной формы такие интегралы могут быть найдены численными методами.

Экспериментально момент инерции тела можно определить, например, с помощью трифилярного подвеса. Трифилярный подвес, изображенный на рисунке 1, представляет собой круглую платформу,

Рис. 1. Трифилярный подвес.

подвешенную на трех симметрично расположенных нитях. Верхние концы нитей прикреплены к неподвижному диску, диаметр которого меньше диаметра платформы. Если на платформу положить тело и повернуть ее на небольшой угол вокруг вертикальной оси, то платформа начнет совершать крутильные колебания вокруг вертикальной оси ОО. Период этих колебаний зависит от момента инерции тела и платформы. Определив период, можно рассчитать момент инерции изучаемого тела.

Рассчитаем период малых крутильных колебаний платформы с помещенным на нее телом (тело на рисунке не изображено). При повороте платформы нити, на которых она подвешена, отклоняются от положения

равновесия, при этом возникает момент сил М относительно оси ОО, стремящийся вернуть платформу в положение равновесия.

На рисунке 2 платформа и одна из нитей подвеса АВ изображены в положении равновесия (штриховая линия) и в положении, когда платформа повернута на угол  (сплошная линия).

Р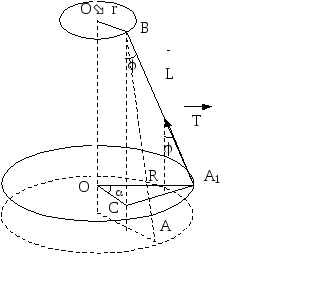 ис.2. Платформа в состоянии равновесия и при повороте на угол .

Движение платформы вокруг оси ОО описывается уравнением:

J= M, (3)

где J – момент инерции платформы и тела относительно этой оси, – ее угловое ускорение.

Период колебаний можно рассчитать из уравнения (3), но для этого надо знать зависимость момента сил М от угла поворота .

На платформу действуют сила тяжести и силы натяжения трех нитей. Величина момента силы тяжести относительно оси ОО равна нулю. Найдем зависимость момента сил натяжения нитей от угла поворота  относительно оси ОО.

Рассмотрим сначала одну нить. Пусть сила ее натяжения равна Т. Момент этой силы М₁ относительно оси ОО равен произведению проекции силы на плоскость платформы Tsin на плечо ОС, длина которого r равна расстоянию от оси вращения до точек крепления нитей на верхнем диске (см. рисунок 2),

. (4)

Из треугольников СОА₁ и СВА₁, у которых одна сторона СА₁ общая, следует, что

,

где R – расстояние от оси вращения до точки крепления нити на платформе, L–длина нити.

При малых колебаниях можно считать, что sin. В этом приближении последнее выражение принимает вид

. (5)

Тогда из уравнений (4) и (5) следует, что момент силы натяжения нити равен

.

При малых углах поворота платформы можно считать, что

(6)

и

(7)

где т – масса платформы с грузом, Н – расстояние между верхним диском и платформой в состоянии равновесия.

Учитывая, что момент натяжения всех нитей М втрое больше М₁, а также (6) и (7), получим:

.

Перед тем как подставить полученное выражение для момента сил М в уравнение (3), нужно обратить внимание на то, что момент сил, возникающий при повороте платформы, стремится вернуть платформу в положение равновесия. Поэтому моменту сил М и угловому смещению  нужно приписать противоположные знаки, т.е.

. (8)

Тогда уравнение (3) с учетом (8) можно записать в виде:

.

Данное уравнение описывает гармонические колебания платформы

,

период которых равен

.

Таким образом, зная параметры установки и экспериментально определив период колебаний платформы Т, можно рассчитать момент инерции:

. (9)

Напомним, что в этой формуле R и r – расстояния от оси вращения до точек крепления нитей соответственно на платформе и верхнем диске.

Формула (9) может быть использована для определения величины момента инерции J₀ пустой платформы (в этом случае т – масса платформы) и величины момента инерции J₁ платформы с помещенным на нее телом (т – сумма масс платформы и тела). Зная J₁ и J₀, можно определить момент инерции тела J₂ относительно оси вращения платформы:

J₂=J₁– J₀ .

Передвигая тело по платформе, можно проверить теорему Штейнера, соглано которой момент инерции тела J относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс тела J_c и параллельной данной оси, и произведения массы тела т на квадрат расстояния между осями а²:

.

В данной работе на платформу помещаются два тела цилиндрической формы массой т₀ каждый, поэтому теорему Штейнера в используемых нами обозначениях можно записать в виде:

, (10)

где J_2с – момент инерции цилиндров относительно оси, проходящей через центр масс.

Экспериментальная часть.

Упражнение 1. Определение момента инерции пустой платформы.

С помощью секундомера определите время 50 колебаний пустой платформы. Крутильные колебания сообщаются платформе поворотом верхнего диска при помощи рукоятки, связанной с ним. Этим достигается почти полное отсутствие других типов колебаний (некрутильных).

Рассчитав период колебаний и используя формулу (9), определите величину момента инерции пустой платформы J₀. Сравните полученное значение с теоретическим, рассчитанным по формуле (2).

Упражнение 2. Проверка теоремы Штейнера.

Располагая тела на платформе симметрично относительно оси вращения, определите (так же, как и в упражнении 1) момент инерции платформы с разнесенными телами J₁(а). Вычитая из полученного значения величину момента инерции пустой платформы J₀, определите момент инерции тел J₂(а) относительно оси вращения. Измерения провести для пяти значений расстояния а.

Постройте график зависимости J₂ от а². Определите угловой коэффициент полученной прямой и сравните с теоретическим значением, который, как это следует из (10), должен быть равен массе двух тел – 2т₀.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.

1. САВЕЛЬЕВ И.В. Курс физики. М., Наука, 1989, т.1, § 31–33,

т.2, § 64, 65.