!Механика и электродинамика / Лабораторные работы / LAB9

8

Л а б о р а т о р н а я р а б о т а № 9.

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ПЛОСКОГО ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО РАЗЛИЧНЫХ ОСЕЙ.

Цель работы: экспериментальное определение момента инерции тонкой плоскопараллельной пластины относительно трех взаимно перпендикулярных осей с помощью трифилярного подвеса.

Оборудование: установка, миллиметровая линейка, секундомер.

Продолжительность: 4ч.

Описание установки. Теоретическая часть.

Момент инерции это величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением :

, (1)

где  m_i –элементарные массы тела, r_i – их расстояния от оси вращения.

Момент инерции тела относительно какой-либо оси можно найти вычислением или измерить экспериментально. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла:

, (2)

где dm и dV – масса и объем элемента тела, находящегося на расстоянии r от интересующей нас оси,  – плотность тела. Интегрирование должно производиться по всему объему тела.

Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы. Например,

для плоскопараллельной пластины можно получить следующую формулу для нахождения величины момента инерции относительно оси, перпендикулярной ее плоскости и проходящей через центр масс пластины:

, (3)

где m–масса, a и b–длины сторон пластины.

Для тел неправильной формы такие интегралы могут быть найдены численными методами.

Экспериментально момент инерции тела можно определить, например, с помощью трифилярного подвеса. Трифилярный подвес, изображенный на рисунке 1, представляет собой круглую платформу,

Рис. 1. Трифилярный подвес.

подвешенную на трех симметрично расположенных нитях. Верхние концы нитей прикреплены к неподвижному диску, диаметр которого меньше диаметра платформы. Если на платформу положить тело и повернуть ее на небольшой угол вокруг вертикальной оси, то платформа начнет совершать крутильные колебания вокруг вертикальной оси ОО. Период этих колебаний зависит от момента инерции тела и платформы. Определив период, можно рассчитать момент инерции изучаемого тела.

Рассчитаем период малых крутильных колебаний платформы с помещенным на нее телом (тело на рисунке не изображено). При повороте платформы нити, на которых она подвешена, отклоняются от положения

равновесия, при этом возникает момент сил М относительно оси ОО, стремящийся вернуть платформу в положение равновесия.

На рисунке 2 платформа и одна из нитей подвеса АВ изображены в положении равновесия (штриховая линия) и в положении, когда платформа повернута на угол  (сплошная линия).

Р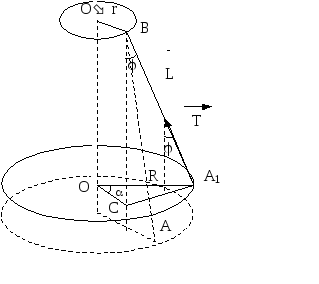 ис.2. Платформа в состоянии равновесия и при повороте на угол .

Движение платформы вокруг оси ОО описывается уравнением

J= M, (4)

где J – момент инерции платформы и тела относительно этой оси, – ее угловое ускорение.

Период колебаний можно рассчитать из уравнения (4), но для этого надо знать зависимость момента сил М от угла поворота .

На платформу действуют сила тяжести и силы натяжения трех нитей. Величина момента силы тяжести относительно оси ОО равна нулю. Найдем зависимость момента сил натяжения нитей относительно оси ОО от угла поворота .

Рассмотрим сначала одну нить. Пусть сила ее натяжения равна Т. Момент этой силы М₁ относительно оси ОО равен произведению проекции силы на плоскость платформы Tsin на плечо ОС, длина которого r равна расстоянию от оси вращения до точек крепления нитей на верхнем диске (см. рисунок 2),

. (5)

Из треугольников СОА₁ и СВА₁, у которых одна сторона СА₁ общая, следует, что

,

где R – расстояние от оси вращения до точки крепления нити на платформе, L–длина нити.

При малых колебаниях можно считать, что sin. В этом приближении последнее выражение принимает вид:

. (6)

Тогда из уравнений (5) и (6) следует, что момент силы натяжения нити равен:

.

При малых углах поворота платформы можно считать, что

(7)

и

(8)

где т – масса платформы с грузом, Н – расстояние между верхним диском и платформой в состоянии равновесия.

Учитывая, что момент натяжения всех нитей М втрое больше М₁, а также (7) и (8), получим:

.

Перед тем как подставить полученное выражение для момента сил М в уравнение (4), нужно обратить внимание на то, что момент сил, возникающий при повороте платформы, стремится вернуть платформу в положение равновесия. Поэтому моменту сил М и угловому смещению  нужно приписать противоположные знаки, т.е.

. (9)

Тогда уравнение (4) с учетом (9) можно записать в виде:

.

Данное уравнение описывает гармонические колебания платформы

,

период которых равен:

.

Таким образом, зная параметры установки, и экспериментально определив период колебаний платформы Т, можно рассчитать момент инерции:

. (10)

Напомним, что в этой формуле R и r – расстояния от оси вращения до точек крепления нитей соответственно на платформе и верхнем диске.

Формула (10) может быть использована для определения величины момента инерции J₀ пустой платформы (в этом случае т – масса платформы) и величины момента инерции J₁ платформы с помещенным на нее телом (т – сумма масс платформы и тела). Зная J₁ и J₀, можно определить момент инерции тела J₂ относительно оси вращения платформы:

J₂=J₁– J₀ .

В данной работе определяются моменты инерции тонкой плоскопараллельной пластины относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке (рис.3). Если оси X и Y лежат в плоскости пластины, а ось Z перпендикулярна ей, то момент

Р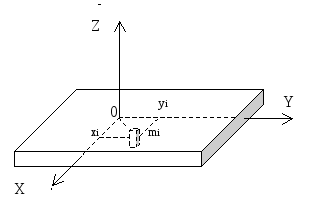 ис.3 Плоскопараллельная пластина.

инерции тонкой пластины относительно этих осей связаны соотношением:

(11)

Отметим, что это выражение справедливо для плоского тела любой формы. Докажем справедливость выражения (11). Если пластина тонкая, то можно считать, что все вещество распределено в плоскости XY, поэтому координаты z всех точек пластины равны нулю. Выделим в пластине материальную точку массой m_i (см. рис.3) с координатами (x_i, y_i,0). Моменты инерции этой точки относительно осей X, Y и Z равны соответственно:

, (12)

, (13)

. (14)

Сложим уравнения (12) и (13)

. (15)

Сравнивая правую часть выражения (15) с уравнением (14), получим

.

Просуммируем правую и левую части этого уравнения по всему объему пластины

.

Воспользовавшись определением момента инерции тела (1), получим:

,

что и требовалось доказать.

В работе проверяется справедливость соотношения (11).

Экспериментальная часть.

Упражнение 1. Определение момента инерции пустой платформы.

С помощью секундомера определите время 50 колебаний пустой платформы. Крутильные колебания сообщаются платформе поворотом верхнего диска при помощи рукоятки, связанной с ним. Этим достигается почти полное отсутствие других типов колебаний (некрутильных).

Рассчитав период колебаний и используя формулу (10), рассчитайте момент инерции пустой платформы J₀. Сравните полученное значение с теоретическим, рассчитанным по формуле :

,

где R₀ – радиус платформы.

Упражнение 2. Определение моментов инерции пластины и проверка соотношения (11).

Располагая пластину на платформе тремя различными способами, определите (так же, как и в упражнении 1) моменты инерции пластины с платформой. Вычитая из полученных значений величину момента инерции пустой платформы, рассчитайте моменты инерции пластины J_x, J_y и J_z. Сравните величину момента инерции пластины J_z с теоретическим значением, рассчитанным по формуле (3).

Проверьте соотношение (11), которое должно выполняться в пределах погрешности.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.

1. САВЕЛЬЕВ И.В. Курс физики. М., Наука, 1989. Т.1, § 31–33,

Т.2, § 64, 65.