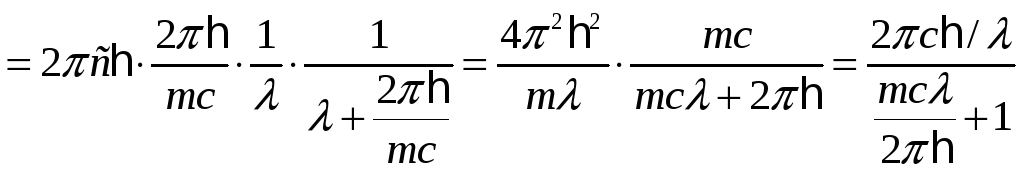!Оптика и квантовая механика / Задачи / 11 / zan15_16

Занятия 15, 16.

№5.278

Точечный изотропный источник испускает свет с . Световая мощность источника . Найти:

а) среднюю плотность потока фотонов на расстоянии ;

б) расстояние от источника до точки, где средняя концентрация фотонов ;

Решение:

а) По определению плотность потока фотонов находится по формуле:

,

где - концентрация фотонов. Найдем ее. Так как источник обладает постоянной мощностью, в любом шаровом слое толщиной (именно такое расстояние проходит фотон за время ) суммарная энергия фотонов будет выражаться по формуле:

.

Зная что, средняя плотность фотонов в таком слое , объем такого слоя и энергия одного фотона , можно найти суммарную энергию фотонов в таком слое:

.

Приравняв значения и вспомнив, что , получим , тогда

. 

б) Из 

№5.280 Лазер излучил в импульсе длительностью пучок света с энергией . Найти среднее давление такого светового импульса, если его сфокусировать в пятнышко диаметром на поверхность, перпендикулярную к пучку, с коэффициентом отражения .

Решение:

По определению, давление ищется по формуле

,

где - сила, действующая на преграду, а - площадь поверхности, на которую падает пучок. Из условия ясно, что площадь поверхности равна:

.

Сила давления возникает за счет изменения импульса пучка при столкновении, тогда импульс пучка до столкновения , а после столкновения (потому что отразилась только часть пучка). С учетом того, что импульсы направлены в противоположные стороны, получаем

.

Тогда

. 

№5.283

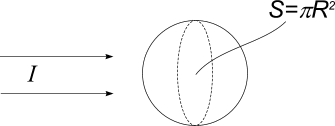
Плоская световая волна интенсивности освещает шар с абсолютно зеркальной поверхностью. Радиус шара . Найти с помощью корпускулярных представлений силу светового давления, испытываемую пластинкой.

Решение:

Э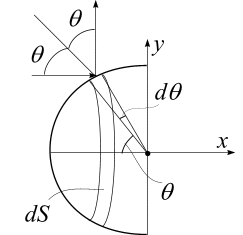нергия волны, падающей на поверхность шара за время будет выражаться по формуле

.

Волна будет давить на шар за счет изменения импульса фотонов. Так как поверхность симметричная, и волна освещает шар равномерно, то можно не учитывать - составляющую импульса отраженных частиц (суммарный импульс вдоль оси после отражения будет равняться 0, а сила будет направлена вдоль оси ). Поскольку поверхность абсолютно зеркальная и имеет шарообразную форму, то изменение импульса одного фотона вдоль оси при ударе о кольцо на шаре площади расположенного под углом и шириной будет иметь вид:

.

Известно, что импульс одного фотона вычисляется по формуле . За время на наше кольцо площадью падает фотонов. Площадь кольца будет равняться произведению длины окружности на ширину полоски :

.

Для нахождения результирующей силы проинтегрируем по половине поверхности шара:

. 

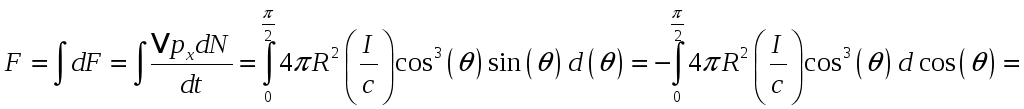
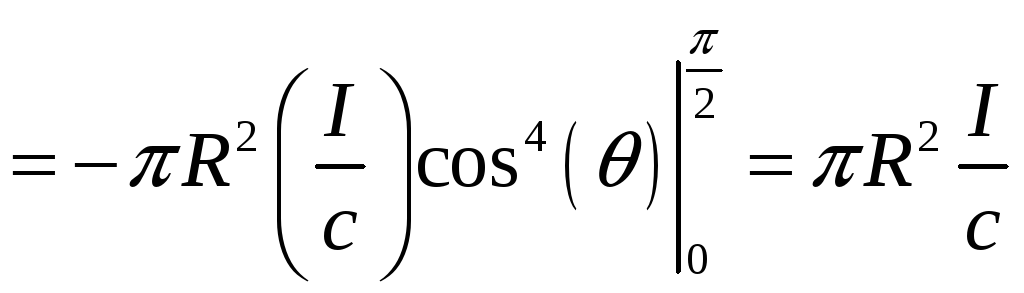№5.290

Найти длину волны коротковолновой границы сплошного рентгеновского спектра, если скорость электронов, подлетающих к антикатоду трубки, , где с – скорость света.

Решение:

Причина рентгеновского спектра: электрон, подлетая к антикатоду, тормозит, т.е. движется с ускорением. А любая частица, движущаяся с ускорением, излучает. Причем длину волны коротковолновой границы будем наблюдать в том случае, когда электрон затормозит перед самой границей антикатода. Значит, кинетическая энергия электронов в трубке из релятивистских соображений:

,

или из волновых свойств частиц:

,

тогда приравняв эти два выражения:



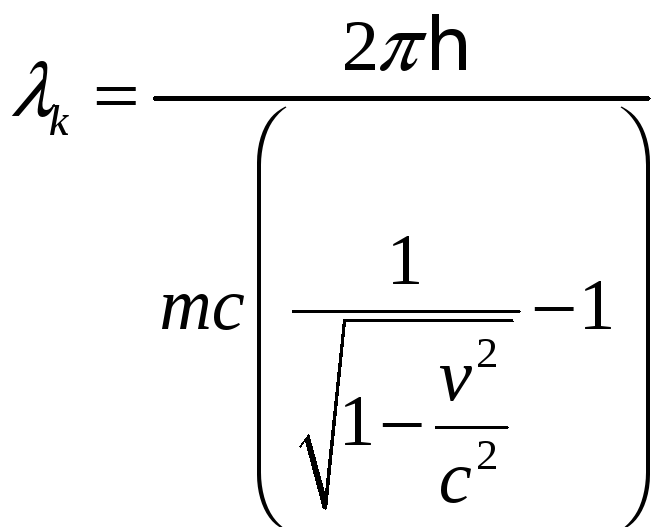
№5.293

При поочередном освещении поверхности некоторого металла светом с длинами волн и обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в раза. Найти работу выхода с поверхности этого металла.

Решение:

Энергия фотона уходит на то, чтобы выбить электрон и сообщить ему какую-то скорость:

, где

Тогда при освещении светом с двумя разными длинами волн:

и

Подставляя второе в первое и вспоминая, что такое , получаем:



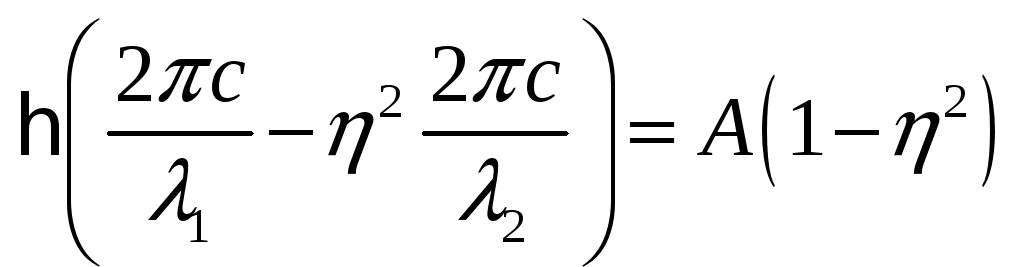
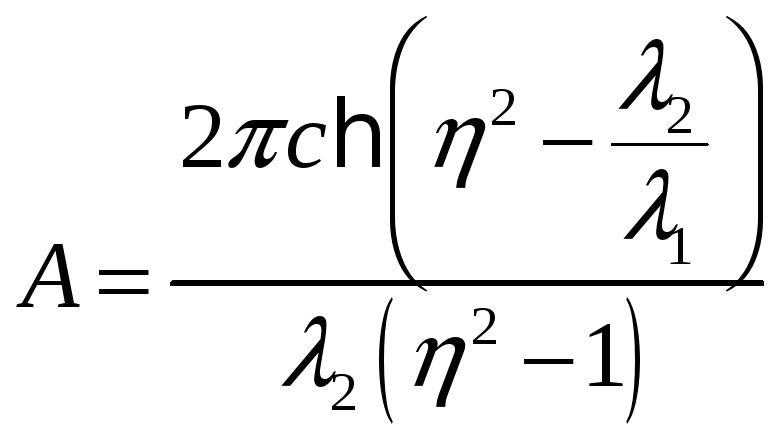
№5.298 Фототок, возникающий в цепи вакуумного фотоэлемента при освещении цинкового электрода электромагнитным излучением с длиной волны прекращается, если подключить внешнее задерживающее напряжение . Найти величину и полярность внешней контактной разности потенциалов фотоэлемента.

Решение:

Для того чтобы внешнее задерживающее напряжение было > 0, система должна выглядеть так, как изображено на рисунке. Т.е. энергия падающих фотонов полностью расходуется на работу выхода электронов из металла и на противодействие внешнему напряжению, т.е.

,

где - максимальная энергия, которую может получить электрон; с учетом того, что она полностью гасится внешним полем, можно записать:

,

где - разность потенциалов между катодом и анодом, возникающая в результате фотоэффекта; контактная разность потенциалов - разность потенциалов, возникающая между двумя разнородными проводниками при их соприкосновении, т.е. его тоже нужно скомпенсировать внешним напряжением:

О направлении контактного напряжения можно судить по ее знаку, полученному после подсчетов. Если получим знак «+» - оно сонаправлено с , т.е. противонаправлено внешнему напряжению (судя по ответу, так и есть). 

№5.304

Фотон с длиной волны рассеялся под прямым углом на покоившемся свободном электроне. Найти: а) частоту рассеянного фотона;

б) кинетическую энергию электрона отдачи;

Решение:

а) Из формулы эффекта Комптона, , где ; в нашей задаче , тогда



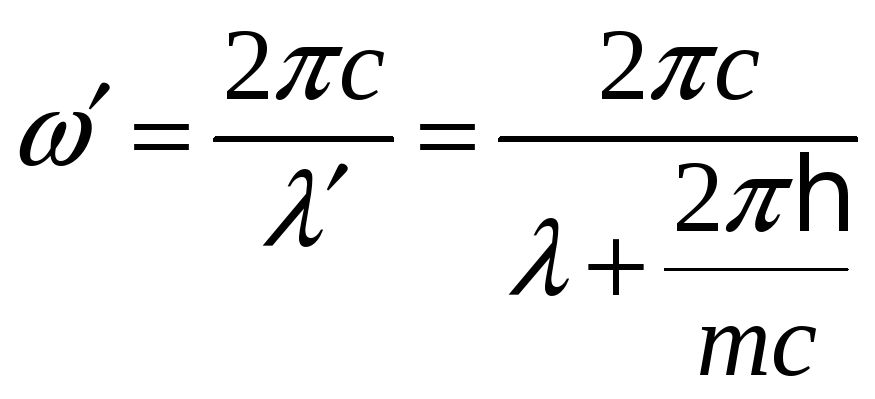
б) Кинетическая энергия электрона отдачи – это разница между его полной энергией после рассеяния на нем фотона (эта энергия включает в себя энергию ) и той самой энергией , которой обладал покоящийся электрон: . Из закона сохранения энергии:

