Тема: 1.4Чертеж многогранника. Чертеж поверхности вращения

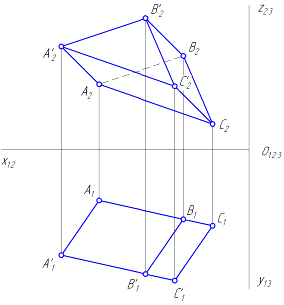
На рисунке показан двухкартинный комплексный чертеж …

			наклонной трехгранной призмы
			прямой трехгранной призмы
			трехгранной пирамиды
			четырехгранной пирамиды

Решение: На чертеже показана наклонная трехгранная призма, которая имеет три боковые грани и основаниями которой являются равные треугольники АВС  и A’B’C’. В название призмы вводят число ее боковых граней, поэтому в данном случае призма называется трехгранной. Так как боковые ребра не перпендикулярны основанию, то призма является наклонной. Королев, Ю. И. Начертательная геометрия : учеб. для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с.

Тема:1.4 Чертеж многогранника. Чертеж поверхности вращения

Геометрическим элементом, вращением отрезка вокруг которого получена поверхность прямого кругового конуса, является …

			прямая i
			точка S
			прямая SB
			точка В

Решение: На рисунке показан двухкартинный комплексный чертеж прямого кругового конуса. Поверхность конуса получена вращением образующей SВ вокруг горизонтально-проецирующей линии – оси вращения i.

Тема:1.4 Чертеж многогранника. Чертеж поверхности вращения

Не относится к поверхностям вращения фигура, показанная на чертеже  …

Решение: Поверхность, образованная вращением образующей вокруг неподвижной оси, называется поверхностью вращения. Наклонный цилиндр не может быть получен вращением вокруг неподвижной оси. Королев, Ю. И. Начертательная геометрия : учеб. для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с.