Тема: 2.1Параллельность на чертеже

Две параллельные прямые изображены на рисунке …

Решение: Если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой.

Тема: 2.1Параллельность на чертеже

Если две плоскости параллельны, то две ___ прямые одной плоскости  параллельны двум пересекающимся прямым другой плоскости.

			пересекающиеся
			параллельные
			скрещивающиеся
			проецирующие

Решение: Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил. Тема:2.1 Параллельность на чертеже

Две прямые параллельны в пространстве, если их одноименные проекции  …

			параллельны
			перпендикулярны
			пересекаются
			принадлежат одной плоскости

Решение: Две прямые параллельны в пространстве, если их одноименные проекции параллельны.

Тема:2.1 Параллельность на чертеже

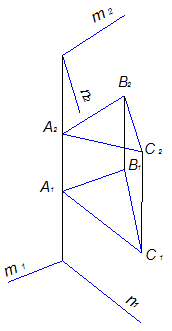
Две параллельные плоскости изображены на рисунке …

Решение: Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. На чертеже заданы две плоскости: одна плоскость задана треугольником АВС, а другая – двумя пересекающимися прямыми m и  n. Прямая m параллельна прямой АВ, а прямая n параллельна прямой АС. Так как прямые АВ и АС  также пересекаются, то заданные на чертеже плоскости параллельны между собой. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема:2.1 Параллельность на чертеже

Прямая a параллельна плоскости на рисунке …

Решение: Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости. На представленном чертеже заданы прямая а и плоскость (m∩n). Прямая а параллельна заданной на чертеже плоскости, так как она параллельна прямой n, лежащей в этой плоскости. Плоскость на рисунке задана двумя пересекающимися прямыми m и n. На чертеже прямая а имеет горизонтальную проекцию а₁, параллельную горизонтальной проекции прямой  n₁, а фронтальная проекция прямой а₂  параллельна фронтальной проекции прямой n₂ , где n принадлежит заданной плоскости. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема: 2.1Параллельность на чертеже

Прямая параллельна плоскости, если она ____ прямой(-ым), лежащей(-им) в этой плоскости.

			параллельна
			перпендикулярна
			пересекается с
			скрещивается с

Решение: Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема: 2.2Принадлежность точки и линии плоскости и поверхности

Плоскости Σ(m∩n) принадлежат точки …

			B и D
			А и С
			А и В
			А и D

Решение: Если точка принадлежит плоскости, то одноименные проекции этой точки лежат на одноименных проекциях прямой, принадлежащей плоскости. Плоскость, изображенная на чертеже, профильно-проецирующая. Все точки, принадлежащие этой плоскости, проецируются на вырожденную (профильную) проекцию этой плоскости. На представленном чертеже это точки B и D.