Тема: 3.1Способ прямоугольного треугольника

Угол наклона отрезка прямой СВ к плоскости проекций П₂ ­ это угол …

			α
			β
			γ
			δ

Решение: Угол наклона отрезка прямой СВ к плоскости проекций определяется как угол между проекцией этого отрезка и отрезком, равным его натуральной величине. Если требуется определить угол наклона прямой к фронтальной плоскости проекций П₂, то необходимо находить натуральную величину отрезка прямой на плоскости П₂. На чертеже это угол α (угол между фронтальной проекцией отрезка С₂В₂ и его натуральной величиной С₂В₀).

Тема: 3.1Способ прямоугольного треугольника

Угол α на чертеже – это угол наклона отрезка прямой СВ к плоскости проекций …

			П2
			П1
			П3
			П4

Решение: Угол наклона отрезка прямой СВ к плоскости проекций определяется как угол между проекцией этого отрезка и отрезком, равным его натуральной величине. На чертеже угол α – это угол между фронтальной проекцией отрезка С₂В₂ и его натуральной величиной С₂В₀. Поскольку  натуральная величина отрезка прямой определена на плоскости П₂, то найденный угол есть угол наклона отрезка прямой СВ к плоскости проекций П₂.

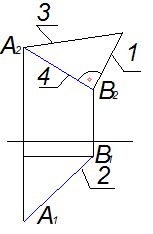
Тема: 3.1Способ прямоугольного треугольника

Натуральная величина отреза прямой АВ – это длина отрезка, обозначенного на чертеже цифрой …

			3
			2
			1
			4

Решение: Натуральная величина отрезка прямой, определенная способом прямоугольного треугольника (обозначена на чертеже цифрой 3), равна гипотенузе прямоугольного треугольника, один из катетов которого равен проекции отрезка (обозначен цифрой 4), а второй есть разность расстояний концов этого отрезка до той же плоскости проекций (обозначена на чертеже цифрой 1). Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема: 3.1Способ прямоугольного треугольника

Угол наклона отрезка прямой АВ к плоскости проекций П₁ – это угол …

			a
			b
			d
			f

Решение: Угол наклона отрезка прямой АВ к плоскости проекций определяется как угол между проекцией этого отрезка и отрезком, равным его натуральной величине. На рисунке проиллюстрирован способ прямоугольного треугольника, который позволяет определить угол наклона отрезка прямой к плоскости проекций. На приведенной иллюстрации угол наклона – угол а. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.