Тема:2.4 Пересечение поверхностей

Поверхности  заданных на чертеже  цилиндров пересекаются по …

			прямым линиям
			окружностям
			прямой и окружности
			эллипсам

Решение: На чертеже представлены два цилиндра, поверхности которых являются фронтально-проецирующими и на фронтальную плоскость проекций проецируются в окружности, которые, пересекаясь, дадут фронтальные проекции прямых, по которым пересекаются цилиндры. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема:2.4 Пересечение поверхностей

Для построения линии пересечения поверхностей, изображенных на рисунке, применяют способ …

			концентрических сфер
			вспомогательных секущих плоскостей
			замены плоскостей проекций
			эксцентрических сфер

Решение: В данном случае обе пересекающиеся поверхности – это поверхности вращения. Оси вращения этих поверхностей пересекаются и образуют плоскость, параллельную фронтальной плоскости проекций П₂. Для решения задачи целесообразно применить способ концентрических сфер.

Тема: 2.4Пересечение поверхностей

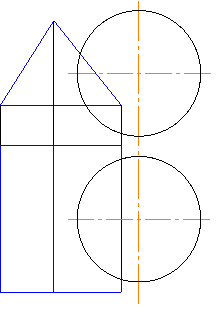
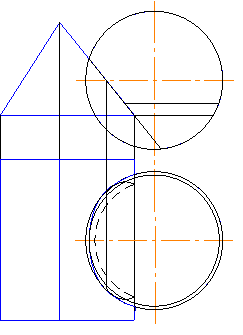
Заданные на чертеже сфера и призма пересекаются по …

			двум окружностям
			окружности и эллипсу
			треугольнику и окружности
			двум эллипсам

Решение: На чертеже представлены сфера и фронтально-проецирующая призма, грани которой пересекают сферу по дугам окружностей. Одна грань, пересекающая призму, является горизонтальной плоскостью уровня, поэтому дуга окружности, принадлежащая ей, проецируется в дугу окружности; эта дуга окружности на горизонтальной проекции невидимая. Вторая грань призмы, пересекающая сферу, является фронтально-проецирующей. Дуга окружности, по которой эта грань пересекает сферу, проецируется в дугу эллипса. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема: 2.4Пересечение поверхностей

Заданные на чертеже конус и призма пересекаются по …

			окружности и эллипсу
			треугольнику и эллипсу
			треугольнику и окружности
			двум эллипсам

Решение: Верхняя грань призмы пересекает конус по окружности, а наклонная (плоскость которой является фронтально-проецирующей и пересекает все образующие конуса) – по эллипсу. Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.