Тема:3.2 Перпендикулярность на чертеже

Две плоскости перпендикулярны на чертеже …

Решение: Две плоскости взаимно перпендикулярны, если одна из них содержит перпендикуляр к другой. В представленной задаче прямая l перпендикулярна к плоскости, заданной двумя пересекающимися прямыми а и в, которые являются линиями уровня заданной плоскости, то есть ее горизонталью (прямая b) и фронталью (прямая а). Королев, Ю. И. Начертательная геометрия : учебник для вузов / Ю. И. Королев. – СПб. : Питер, 2006. – 252 с. : ил.

Тема: 3.2Перпендикулярность на чертеже

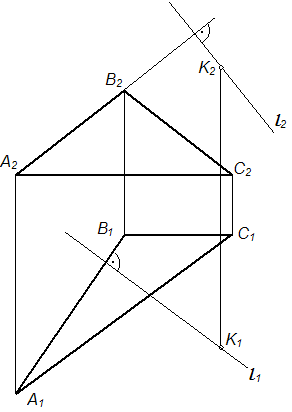
Проекции перпендикуляра l, опущенного из точки К на плоскость Σ (АВС), правильно построены на рисунке …

Решение: Перпендикуляр к плоскости перпендикулярен любой прямой, проведенной в этой плоскости. Из множества этих прямых при построении перпендикуляра к плоскости на чертеже выбирают фронталь и горизонталь плоскости, так как при этом образуются прямые углы, одна из сторон которых параллельна плоскости проекций. Прямая l перпендикулярна плоскости на чертеже, если ее горизонтальная проекция l₁ перпендикулярна горизонтальной проекции горизонтали A₁C₁, а фронтальная проекция прямой l₂ перпендикулярна фронтальной проекции фронтали B₂C₂.

Тема: 3.2Перпендикулярность на чертеже

Прямые, изображенные на чертеже, …

			перпендикулярны
			параллельны
			скрещивающиеся
			проецирующие

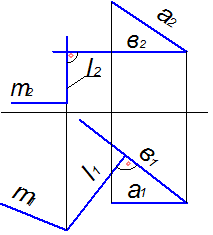
Решение: На чертеже показаны две пересекающиеся прямые. Прямая а параллельна горизонтальной плоскости проекций, то есть проецируется на плоскость П₁ в натуральную величину. Прямой угол, который образуют прямые а и b, на плоскость П₁ проецируется также в натуральную величину. Следовательно, прямые а и b перпендикулярны

Тема: 3.2Перпендикулярность на чертеже

Прямая l, изображенная на чертеже,______плоскости.

			перпендикулярна
			принадлежит
			параллельна
			не перпендикулярна

Решение: Горизонтальная проекция l₁ перпендикулярна горизонтальной проекции горизонтали A₁C₁ заданной плоскости, а фронтальная проекция прямой l₂ перпендикулярна фронтальной проекции фронтали B₂C₂ этой плоскости. Денного  условия достаточно, чтобы прямая l была перпендикулярна плоскости.