Тема:4.1 Образование и задание кривых линий и поверхностей

Линию, перемещающуюся в пространстве и создающую поверхность, называют …

			образующей
			направляющей
			определяющей
			каркасом

Решение: Кривая поверхность может рассматриваться как совокупность всех положений некоторой линии, движущейся в пространстве. Движущуюся линию в этом случае называют образующей поверхности, а линии (иногда и точки), определяющие закон ее перемещения, – направляющими. 1. Гордон, В. О. Курс начертательной геометрии : учеб. пособие / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Высшая школа, 2009. – 272 с. 2. Локтев, О. В. Краткий курс начертательной геометрии : учеб. / О. В. Локтев. – М. : Высшая школа, 2006. – 136 с. 3. Лагерь, А. И. Основы начертательной геометрии : учеб. / А. И. Лагерь, А. Н. Мота, К. С. Рушелюк. – М. : Высшая школа, 2007. – 281 с. 4. Чекмарев, А. А Инженерная графика : учеб. / А. А. Чекмарев. – М. : Высшая школа, 2007. – 382 с.

Тема:4.1 Образование и задание кривых линий и поверхностей

Каркас поверхности состоит из …

			образующих и направляющих
			определяющих и образующих
			направляющих и определяющих
			направляющих и осевых

Решение: Каркасы поверхностей бывают точечные и линейные. Точечным каркасом называется совокупность точек на поверхности, которые достаточно точно определяют эту поверхность. Линейный каркас – это совокупность линий, принадлежащих поверхности. 1. Гордон, В. О. Курс начертательной геометрии : учеб. пособие / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Высшая школа, 2009. – 272 с. 2. Локтев, О. В. Краткий курс начертательной геометрии : учеб. / О. В. Локтев. – М. : Высшая школа, 2006. – 136 с. 3. Лагерь, А. И. Основы начертательной геометрии : учеб. / А. И. Лагерь, А. Н. Мота, К. С. Рушелюк. – М. : Высшая школа, 2007. – 281 с. 4. Чекмарев, А. А Инженерная графика : учеб. / А. А. Чекмарев. – М. : Высшая школа, 2007. – 382 с.

Тема: 4.1Образование и задание кривых линий и поверхностей

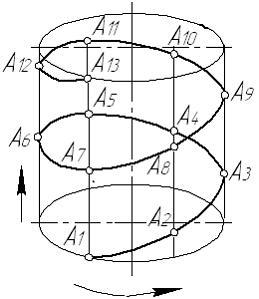
Цилиндрическая винтовая линия образуется при ___ движении точки.

			вращательно-поступательном
			поступательном
			вращательном
			произвольном

Решение: Цилиндрическая винтовая линия (гелиса) – пространственная кривая, представляющая собой траекторию точки, выполняющей винтовое движение. Винтовое движение включает в себя одновременно равномерное поступательное движение точки по прямой и равномерное вращательное движение этой прямой с точкой вокруг оси, которой прямая параллельна. 1. Гордон, В. О. Курс начертательной геометрии : учеб. пособие / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Высшая школа, 2009. – 272 с. 2. Локтев, О. В. Краткий курс начертательной геометрии : учеб. / О. В. Локтев. – М. : Высшая школа, 2006. – 136 с. 3. Лагерь, А. И. Основы начертательной геометрии : учеб. / А. И. Лагерь, А. Н. Мота, К. С. Рушелюк. – М. : Высшая школа, 2007. – 281 с. 4. Чекмарев, А. А Инженерная графика : учеб. / А. А. Чекмарев. – М. : Высшая школа, 2007. – 382 с.