Возмущения стационарных состояний

Пусть система находится в стационарном состоянии | h_i с энергией_i.Проведем измерение значения некоторой наблюдаемойА, оператор которой не коммутирует с гамильтонианом. В результате прохождения через спектральный анализаторАсистема окажется в одном из базисных пучков, т.е. перейдет из начального состояния в конечное:| h_i |А_j. Это конечное состояние не является собственным для гамильтониана и, следовательно, не будет являться стационарным. Попав в это состояние, система начнет эволюционировать и, в конце концов, перейдет в одно из стационарных состояний:

Подобные переходы между стационарными состояниями обычно называются "квантовыми скачками". Это название связано с тем фактом, что каждый такой переход сопровождается поглощением или испусканием строго определенной порции — кванта— энергии:

 = _j – _i =  (_j – _i) = h (_j – _i)

Важной особенностью квантовых скачков является то, что они всегда вызываются внешними факторами — возмущениемисходного стационарного состояния (действие света, электрического или магнитного поля, механических сил и т.д.).

Пространственная зависимость амплитуд

Зависимость амплитуд от пространственного положения прибора-анализатора можно описать совершенно аналогично рассмотренному описанию влияния времени выполнения измерения. Единственное отличие заключается в том, что пространство трехмерно и перемещение прибора в пространстве можно выполнить по-разному.

Произвольное перемещение в пространстве можно осуществить посредством двух последовательных процедур: 1) сдвигавдоль радиуса (изменение расстояния наr) и 2)поворотана некоторый угол(изменение ориентации). Описание любого перемещения может быть получено посредством комбинации описаний таких сдвигов и поворотов.

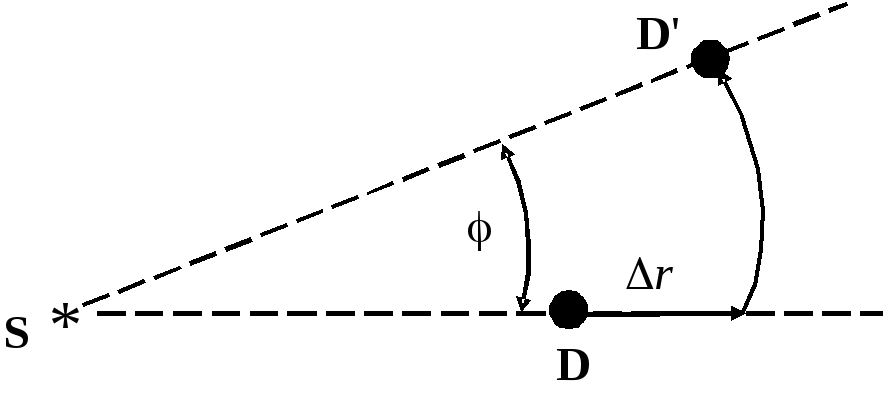
Так же, как в случае со временем, удобно выбрать бесконечно малые("инфинитезимальные") сдвиги (наdr) и повороты (наd). Для этих элементарных перемещений можно определить операторы R(dr)и (d), аналогичные оператору эволюции U(dt):

|   _{(t + dt)} = U(dt) |   _{(t )}

|   _{(r + dr)} = R(dr)|   _{(r ) и} |   _{( + d)} = (d) |   _()

Проведя преобразования, мы получим уравнения, аналогичные уравнению Шредингера:

Аналогами оператора Гамильтона в этих уравнениях являются:

P_r —оператор проекции импульсана направление сдвигаr.

L_ —оператор проекции момента импульсана ось вращения.

У этих операторов имеются собственные векторы (собственные функции):

Параметры входящие в эти выражения представляют собой, с одной стороны, собственные значения операторов, а, с другой стороны, допустимые значения наблюдаемых: p_i — величина проекции импульса на направлениеr,L_i — величина проекции момента импульса на ось вращения.

Собственные состояния операторов PиLотличаются тем, что для них указанные наблюдаемые (PиL) имеют строго определенные значения и выражаются конкретными числами (P_iиL_i), а не функциями распределения. Кроме того, собственные состояния обоих операторов также образуют базисные наборы, которые можно использовать для представления произвольных состояний в виде ЛК.

Одномерность времени приводит к тому, что энергия является скалярнойвеличиной. Пространство имеет три измерения и поэтому новые наблюдаемые можно рассматривать каквекторныевеличины.

Например, сдвиг вдоль произвольного радиус-вектора rможно рассматривать как совокупность трех сдвигов вдоль декартовых осей:

dr = (dx, dy, dz)

В результате можно ввести сразу три оператора проекций импульса и рассматривать их как компоненты одного векторногооператора импульса:

P = (P_x, P_y, P_z)

(Правило применения такого оператора к некоторой функции состоит в том, что эту функцию следует подвергнуть трем отдельным преобразованиям — P_x, P_yи P_z. Следовательно, результатом действия векторного оператора на исходную функцию будут сразу три новых функции, полученные в ходе таких преобразований.)

Любой поворот вокруг произвольной оси можно рассматривать как последовательность поворотов вокруг декартовых осей:

d = (d_x, d_y, d_z)

и ввести три оператора проекций момента импульса, которые можно рассматривать как компоненты одного векторного оператора момента:

L = ( L_x, L_y, L_z)

Иногда используют еще две конструкции:

оператор квадрата импульса P ² = P_x²+P_y²+P_z²

оператор квадрата момента L² = L_x² + L_y² + L_z²

Их собственные значения представляют собой допустимые значения квадрата модуля вектора импульса и квадрата модуля вектора момента импульса, соответственно.

Эти два оператора используются для построения оператора кинетической энергиидля двух видов механического движения:

поступательное движение T = P² / 2m

вращательное движение T = L² / 2I