4. Задачи и упражнения

1. Эйлерово и лагранжево описание движения сплошной среды. Материальная производная

Задача 4.1.1.Поле скоростей задано вектором. Определить скорость и ускорение частицы, находящейся в моментв точке.

Задача 4.1.2.Дан лагранжев закон движения:

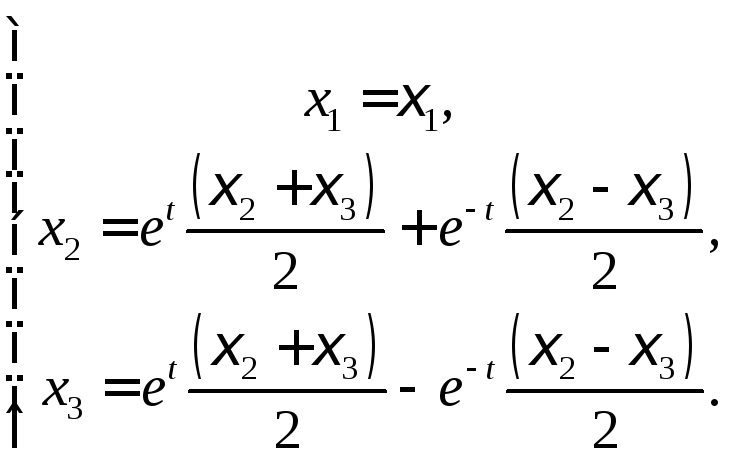
Найти компоненты скорости в эйлеровом описании.

Задача 4.1.3.Дан лагранжев закон движения:

1) Найти якобиан перехода к эйлеровым переменным. 2) Найти скорость в лагранжевых переменных. 3) Найти ускорение в лагранжевых переменных. 4) Перейти к эйлерову описанию (выразить через). 5) Найти якобиан перехода к лагранжевым переменным. 6) Найти скорость и ускорение в эйлеровых переменных. 7) Зная поле скоростей в эйлеровых переменных, перейти к лагранжевому описанию.

Задача 4.1.4.Задано поле скоростей в переменных Лагранжа:

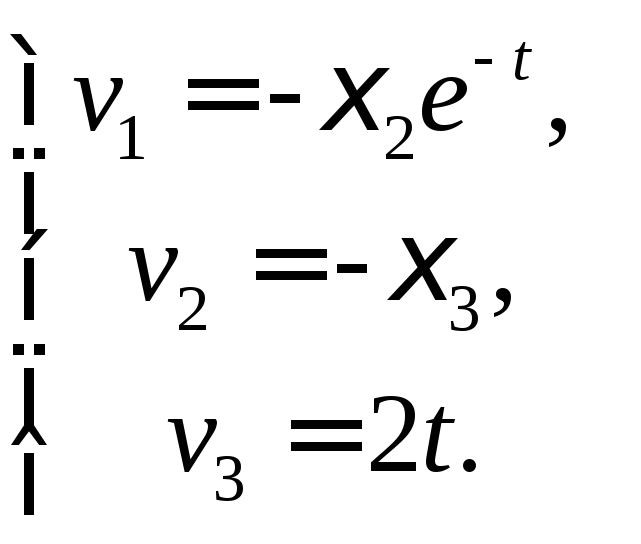
1) Показать, что переход к переменным Эйлера возможен. Найти компоненты скорости и ускорения в переменных Эйлера. 2) Рассматривая поле скоростей в переменных Эйлера, полученное в пункте 1, как условие задачи, перейти к переменным Лагранжа и получить закон движения.

Задача 4.1.5.Задано поле скоростей в переменных Лагранжа:

1) Показать, что переход к переменным Эйлера возможен. Найти компоненты скорости и ускорения в переменных Эйлера. 2) Рассматривая поле скоростей в переменных Эйлера, полученное в пункте 1, как условие задачи, перейти к переменным Лагранжа и получить закон движения.

Задача 4.1.6.Ввести пространственную систему координат и лагранжевы координаты частиц и найти закон движения в следующих случаях:

а) твердое тело движется поступательно со скоростью, постоянной по направлению и имеющей постоянную величину ;

б) твердое тело вращается вокруг неподвижной оси с постоянной угловой скоростью .

Задача 4.1.7.Для поступательных движений твердого тела указать общий вид поля скорости в лагранжевом описании и общий вид закона движения.

Задача 4.1.8.Движение среды происходит по закону

Проверить, что числа для индивидуальной частицы имеют смысл координат,,точки пространства, в которой она находилась в момент. Найти поля скорости и ускорения в лагранжевом описании. Какая частица в момент временинаходится в точке с координатами?

Задача 4.1.9.Движение происходит по закону

.

а) Найти поля скорости и ускорения в лагранжевом описании.

б) Где находится в момент времени частица, которая в моментнаходилась в точке пространства с координатами?

Задача 4.1.10.В моментрассматриваются функции

обратные закону движения

Каков смысл их значений? Чему равны индивидуальные производные ?

Задача 4.1.11.Найти поля скорости и ускорения в лагранжевом и эйлеровом описаниях, если движение среды происходит по закону

а) трехосное растяжение тела:

;

б) простой сдвиг:

;

в) однородная деформация при одновременном вращении тела с закрепленной точкой:

.

Задача 4.1.12.Ввести лагранжевы координаты и найти закон движения сплошной среды, если оно происходит с полем скорости

.

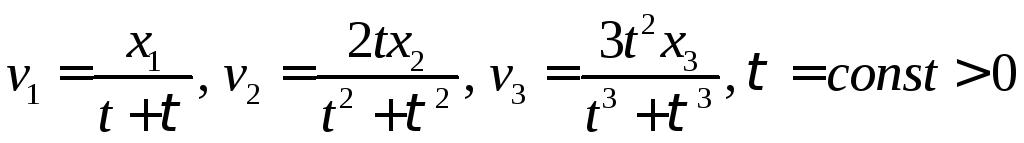Задача 4.1.13.Ввести лагранжевы координаты и найти закон движения сплошной среды, если поле скорости имеет вид:

а) ,,,,;

б) ,,,;

в) ,,,,.

Задача 4.1.14.Задан закон движения сплошной среды

,

,

.

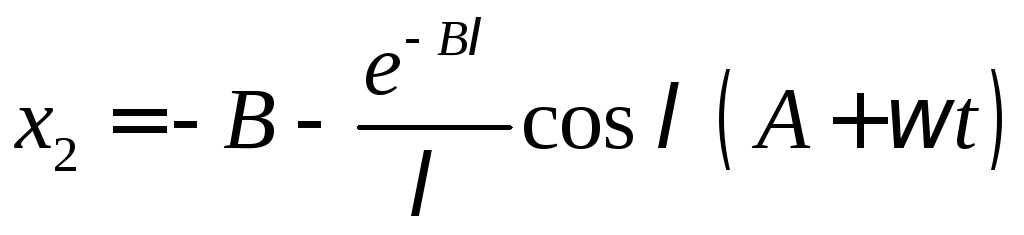Показать, что траектории – окружности, а величина скорости постоянна. Определить также связь между ии константамии.

Задача 4.1.15.Дано поле скоростей в лагранжевом описании

,,.

Найти компоненты ускорения.

Задача 4.1.16.В каком случае материальная производнаянекоторого параметрасовпадает с частной производнойэтого параметра по времени?

Задача 4.1.17.В электромагнитном континууме напряженность магнитного поля равна, гдеи– константа, и движение задано полем скоростей,,. Определить скорость изменения напряженности магнитного поля для частицы, расположенной в моментв точке.

Задача 4.1.18.Напряженность электрического поля в области, занятой движущейся жидкостью, равна, гдеи– константа. Скорость жидкости задана своими компонентами,,. Найтив точке.

Задача 4.1.19.Проверить справедливость формулы

.
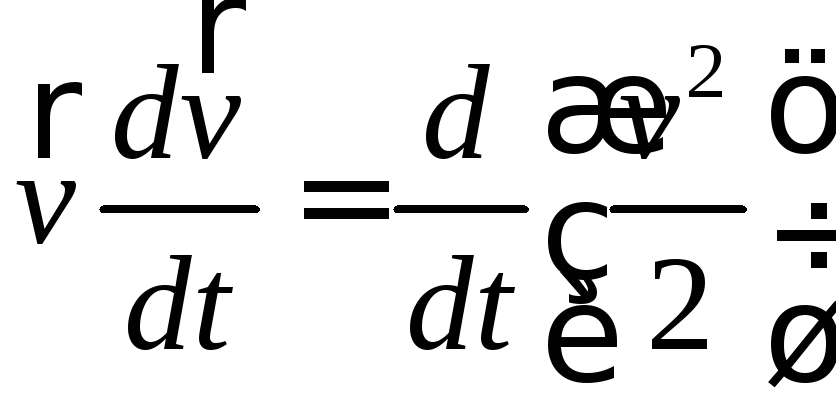