Взаимодействие двух параллельных токов

 

 

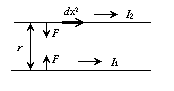
Рис. 2

 

Формула Ампера, определяющая силу, действующую на элемент тока I₂dx₂, находящийся в магнитном поле В₁₂, имеет вид:

 

, (в "СИ")  (7)

билет 37

Сила Лоренца. Электрический заряд в магнитном поле. Эффект Холла.

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечнуюзаряженную частицу

Сила F, действующая на частицу с электрическим зарядом q, движущуюся со скоростью v, во внешнем электрическом E и магнитном B полях, такова:

магнитное поле Действует на электрический ток (сила Ампера).

I - сила тока; B - магнитная индукция; l - длина проводника; α - угол между B и проводником.

Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле

Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца

, Н,                                         (6.11)

где v –скорость носителя; q – его заряд.

Направление силы Лоренца определяется правилом левой руки.

билет 38

Циркуляция вектора магнитной индукции в вакууме. Закон полного тока. Магнитное поле соленоида.

Введем, аналогично циркуляции вектора напряженности электростатического поля, циркуляцию вектора магнитной индукции.Циркуляцией вектора В по заданному замкнутому контуру называется интеграл    где dl — вектор элементарной длины контура, который направлен вдоль обхода контура, B_l=Bcosα — составляющая вектора В в направлении касательной к контуру (с учетом выбора направления обхода контура), α — угол между векторами В и dl. 

 - теорема о циркуляции вектора :

циркуляция вектора по произвольному контуру равна произведениюна алгебраическую сумму токов, охватываемых контуром.

; ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта

Закон полного тока магнитного поля в вакууме: циркуляция вектора индукции магнитного поля постоянного электрического тока вдоль замкнутого контура пропорциональна алгебраической сумме токов, охватываемых этим контуром: ∫В dl = ∫В_l dl = μ₀∑I_k где n - число всех проводников с токами, охватываемых контуром Lпроизвольной формы. Токи считаются положительными, если из конца вектора плотности тока, направленного по оси проводника в сторону тока, обход контура L кажется происходящим против часовой стрелки. В противном случае токи считаются отрицательными. Токи, которые не охватываются контуром L, не влияют на циркуляцию B

Соленоид представляет собой провод, навитый на круглый цилиндрический каркас

Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток.

Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.

.

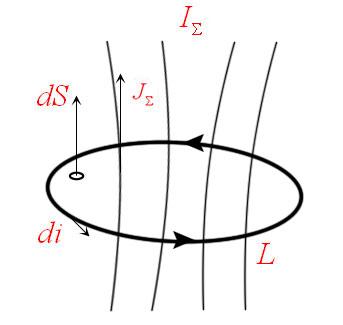
Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток протоивоположного направления считается отрицательным.

Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков.

Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.

билет 39

Поток вектора магнитной индукции. Теорема Гаусса. Работа по перемещению проводника с током в магнитном поле.

Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная:

Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб)

 

Магнитный поток - величина скалярная.

Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность.

Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю:

Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

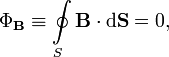
или в дифференциальной форме

Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле^[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.

      Итак,

,

(2.9.1)

      Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

билет 40

Электромагнитная индукция. Закон Фарадея. Вихревые токи. Вращение рамки в магнитном поле.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

 — электродвижущая сила, действующая вдоль произвольно выбранного контура,

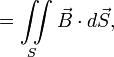  — магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где

 — электродвижущая сила,

 — число витков,

 — магнитный поток через один виток,

 — потокосцепление катушки.

Вихревые токи или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревые индукционные токи, возникающие в проводниках при изменении пронизывающего их магнитного поля.

ВИХРЕВЫЕ ТОКИ, электрический ток, движущийся по кругу; возникает в ПРОВОДНИКЕ под воздействием переменного магнитного поля. Вихревые токи вызывают потерю энергии в ГЕНЕРАТОРАХ и ДВИГАТЕЛЯХ переменного тока, поскольку взаимодействие между вихревыми токами в движущемся проводнике и полем, в котором он движется, замедляет движение проводника.

при вращении проволочной рамки в магнитном поле магнитный поток, пронизывающий рамку, будет периодически изменяться. если к концам вращающейся рамки с помошью скользящих контактов подключить внешнюю нагрузку, то в ней возникнет переменный индукционный ток. амплитуда тока будет зависеть от сопротивления всей цепи. рамка вращающаяся в магнитном поле,является простейшей моделью генератора переменного тока.

билет 41

Взаимная индукция. Индуктивность тороидальной катушки. Трансформаторы.

ВЗАИМНАЯ ИНДУКЦИЯ – явление индуктирования (наведения) эдс индукции в одной цепи (катушке) при изменении электрического тока в другой цепи. Ток I₁, проходя по виткам W ₁ первой катушки, вызывает магнитный поток, часть которого Ф _(1-2) пронизывает витки второй катушки W₂ (рис.), образуя потокосцепление взаимной индукции Y = W₂ Ф _(1-2).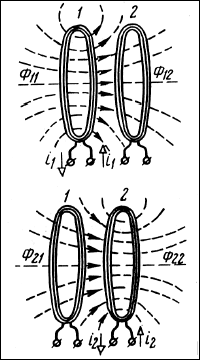

Магнитный поток Ф _1-2 и, следовательно, потокосцепление пропорциональны току Y _1-2 = M ₁ 2 I ₁.

Аналогично ток I₂, проходя по виткам второй катушки, вызывает магнитный поток Ф _2-1, пронизывающий витки первой катушки W ₁, образуя потокосцепление взаимной индукции Y _2-1 = W ₁ Ф _2-1.

Для этого случая потокосцепление пропорционально току Y _2-1 = M _2-1 I ₂.

Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближённо пользоваться формулой для бесконечного прямого соленоида (см. выше):

где - оценка длины соленоида ( - большой радиус тора).

Лучшее приближение дает формулагде предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.

Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанные обмотки на каком-либомагнитопроводе и предназначенное для преобразования посредством электромагнитной индукции одной или нескольких систем (напряжений) переменного или постоянного тока в одну или несколько других систем (напряжений), без изменения частоты^[1].^[2].

Трансформатор осуществляет преобразование напряжения переменного или постоянного тока и/или гальваническую развязку в самых различных областях применения — электроэнергетике, электронике и радиотехнике.

Трансформаторы питания применяются в блоках питания радиоустройств и служат для получения переменных напряжений, необходимых для нормального функционирования аппаратуры.

Согласующие трансформаторы предназначены для изменения уровня напряжений ( токов ) электрических сигналов, несущих полезную информацию.

Импульсные трансформаторы предназначены для формирования и трансформации импульсов малой длительности. Основным требованием, предъявляемым к импульсным трансформаторам, является требование малых искажений формы трансформируемого импульса.

Билет 42

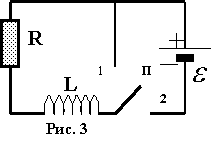
Токи при размыкании и замыкании цепи.

Поставим переключатель "П", рис. 3, в положение 1, разомкнув цепь, тогда

IR = .

Откуда (10)

Это линейное однородное дифференциальное уравнение первого порядка с разделяющимися переменными .

Решением его будет I = I, (11)

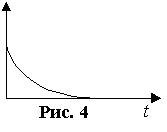
где . График изменения тока при размыкании цепи представлен на рис. 4.