Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 18

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 18

Глава 9

Предельные теоремы теории вероятностей

§ 1. Неравенства Чебышева. Закон больших чисел.

Следующие два неравенства называют неравенствами Чебышева. Сформулируем их в виде теорем.

Теорема: имеют место неравенства:

.

Доказательство:

Разложим в сумму двух слагаемых

,

так как x > 0, получаем

.

.

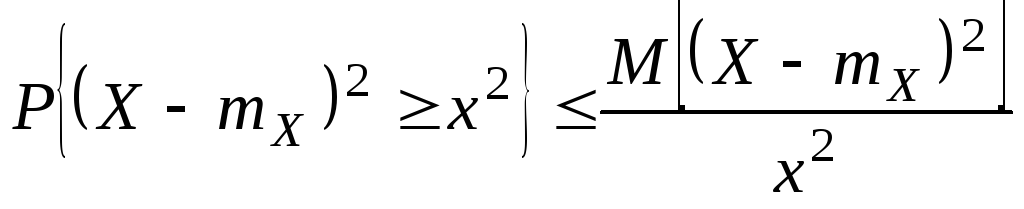
Замечание.

Очень часто второе неравенство Чебышева дают в такой форме

.

Второе неравенство Чебышева показывает, что при малой дисперсии с вероятностью близкой к 1 СВ Х концентрируется около своего МО.

Теорема (Чебышева):

Если – независимы и существует С > 0, такая что , К = 1, 2, …, n, тогда :

Доказательство:

Рассмотрим и применим к СВ второе неравенство Чебышева.

.

.

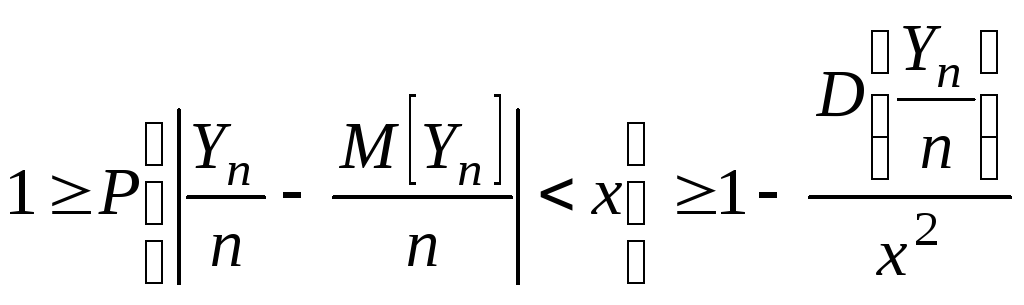В силу аддитивного свойства дисперсии, получаем

,

.

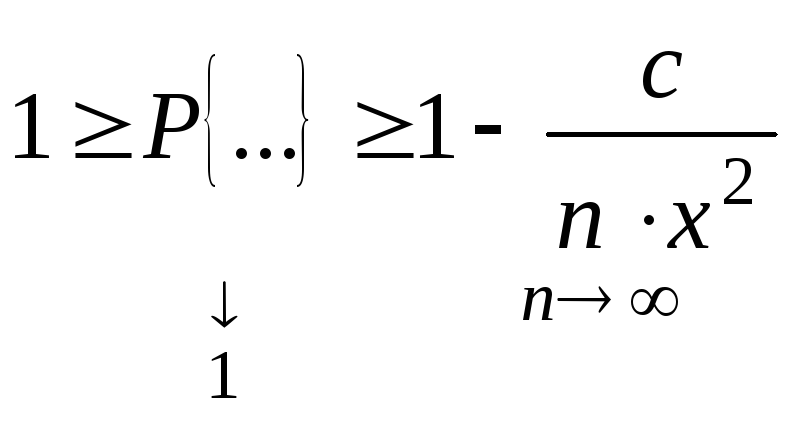
Следствие:

Если – независимы и одинаково распределены, т.е. , а , где k= 1, …, n, тогда

.

Замечание.

Предельные утверждения, сформулированные в теореме Чебышева и следствии к этой теореме носят название закона больших чисел (ЗБЧ). ЗБЧ утверждает, что с вероятностью приближающейся при n к 1, среднее арифметическое независимых слагаемых при определенных условиях становятся близким к константе.

Из утверждения последнего следствия получаем ЗБЧ в схеме Бернулли.

Теорема (Бернулли):

Пусть – число успехов при n независимых испытаниях с вероятностью 0 < p < 1 в каждом испытании, тогда :

.

Доказательство:

Представим в виде суммы независимых СВ , где , или при i-ом испытании произошел успех и , если при i-ом испытании произошел неуспех.

.

Применяя следствие к теореме Чебышева, получаем утверждение к теореме Бернулли.

§ 2. Понятие о теореме Ляпунова. Формулировка центральной предельной теоремы (ЦПТ).

Известно, что нормально распределенные СВ широко распространены на практике, объяснение дал Ляпунов (ЦПТ).

Если СВ Х представляет собой сумму очень большого числа взаимно независимых СВ влияние каждой из которых на всю сумму ничтожно мало, то СВ Х имеет распределение близкое к нормальному.

Приведем формулировку ЦПТ без доказательства.

Теорема (ЦПТ):

Если СВ в последовательности , n = 1, 2, … независимы, одинаково распределены и имеют конечные , , то :

,

где 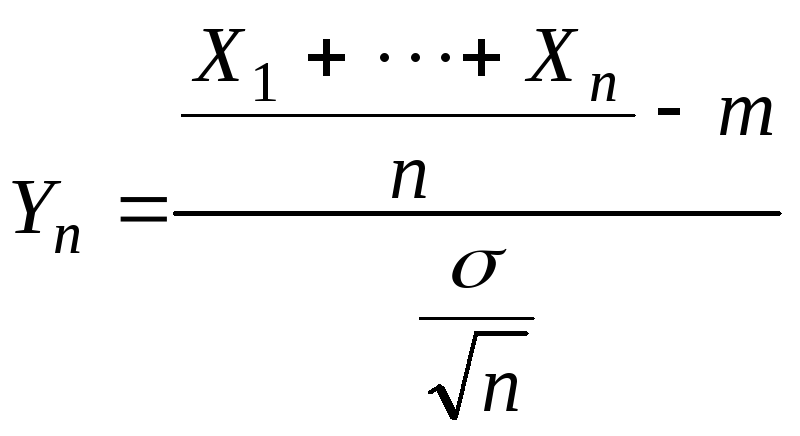– стандартизованное среднее арифметическое, n-независимых СВ в последовательности.

Замечание

Следствиями ЦПТ являются локальная и интегральная теоремы Муавра-Лапласса.

Критерий и его применение.

Критерий применяется в частности для проверки гипотез о виде распределения генеральной совокупности.

Процедура применения критерия для проверки гипотезы H₀, утверждающей, что СВ Х имеет закон распределения состоит из следующих этапов.

Этапы:

1. По выборке найти оценки неизвестных параметров предполагаемого закона .

2. Если Х–СВДТ – определить частоты 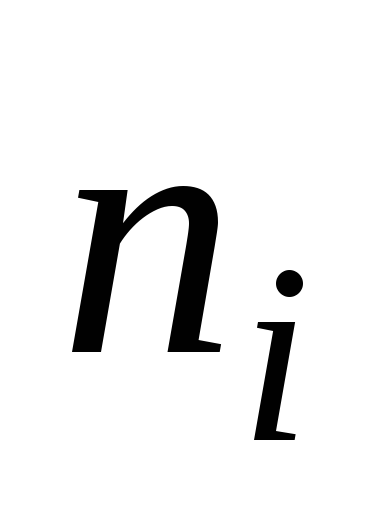, i = 1, 2, …, r, с которым каждое значение встречается в выборке.

Если Х–СВНТ – разбить множество значений на r – непересекающихся интервалов и попавших в каждый из этих интервалов .

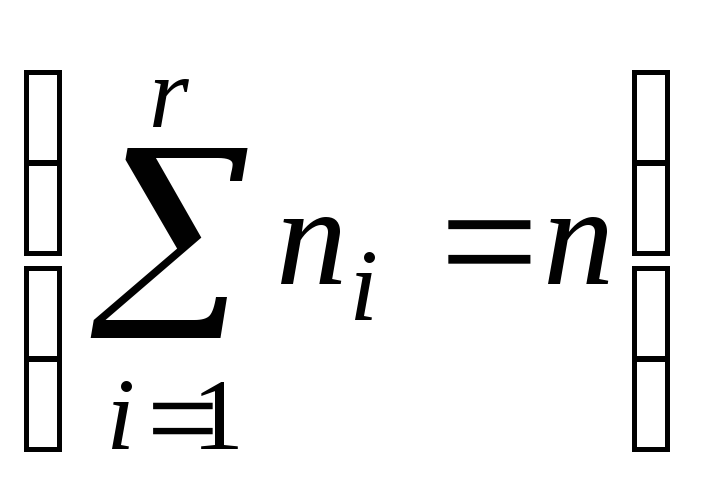3. Х–СВДТ вычислить .

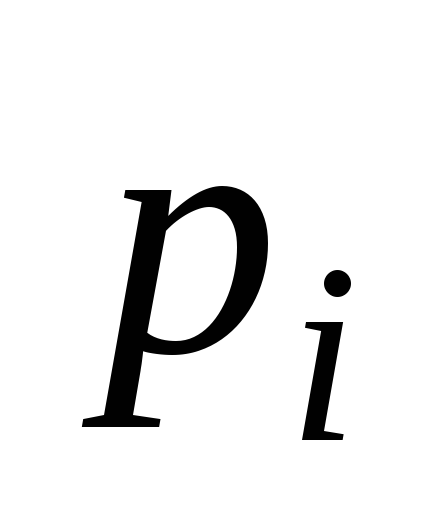Х–СВНТ вычислить .

4. .

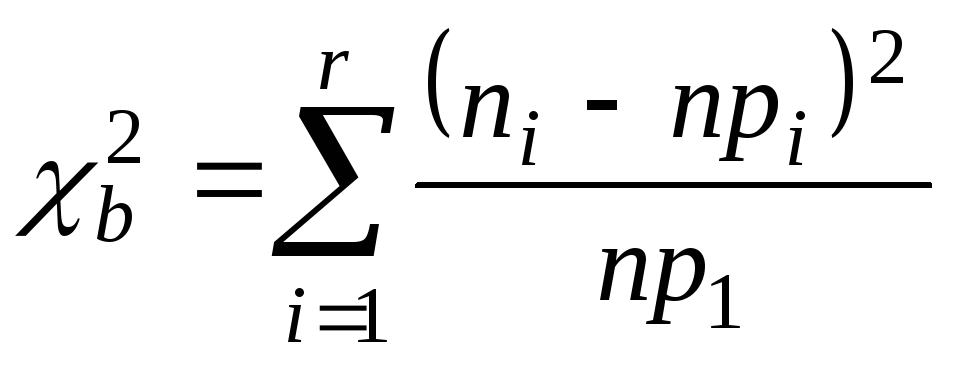5. Принять статистическое решение.

– гипотеза Н₀ – принимается.

– гипотеза Н₀ – отклоняется.

e – количество оцениваемых параметров.

Малочисленные частоты надо будет объединять.

Проверка гипотезы о равномерном распределении генеральной совокупности.

n = 200

А;

№	(xi-1, xi)	ni
1	2 – 4	21	 =0,05
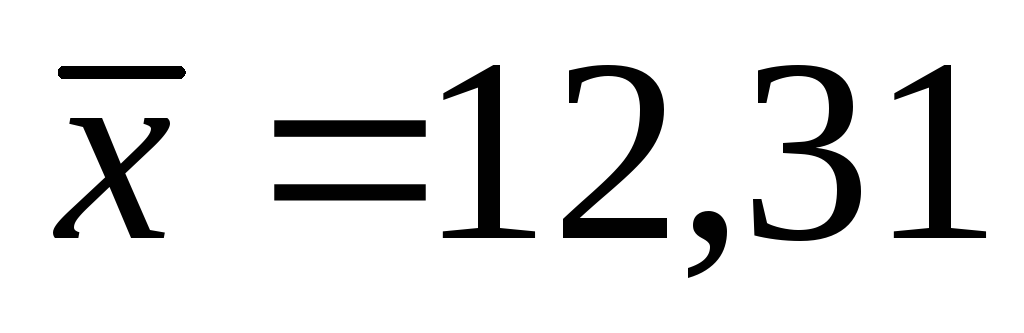
2	4 – 6	16
3	6 – 8	15
4	8 – 10	26
5	10 – 12	22
6	12 – 14	14
7	14 – 16	21
8	16 – 18	22
9	18 – 20	18
10	20 – 22	25

1.

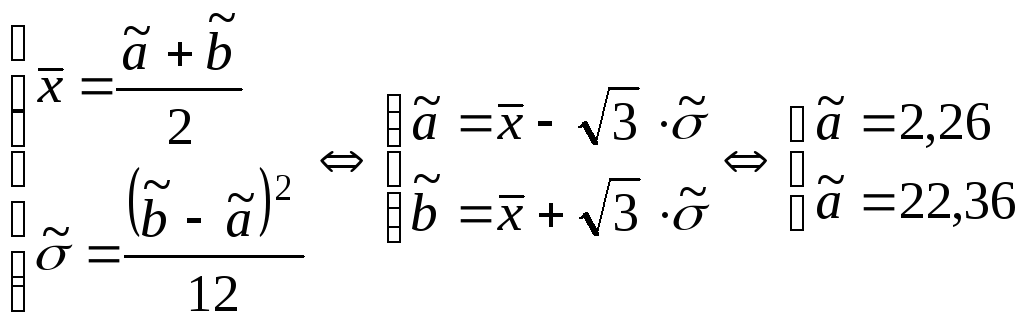
2.

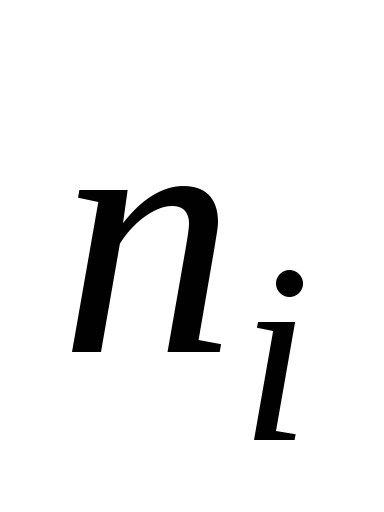
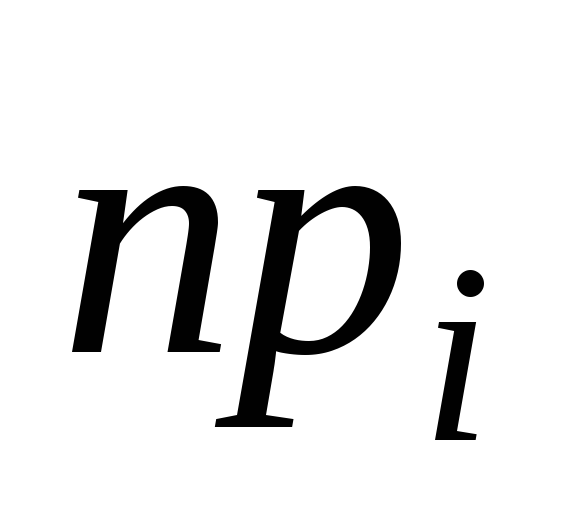
21	17,3	0,79
16	20	0,8

k = 10 – 2 – 1 = 7

– нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.