Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Допечатка 19 лекции

 6.4.2. Основные статики, связанные с выборочными средним и дисперсией, и их законы распределения.

(2)

(3)

Считаем, что генеральная Х~ (1)

Утверждение 19.1. Статика ~N(0,1), если выполнено (1)

- линейная функция от выборки, U – линейное преобразование – стандартизация 

 результат.

Утверждение 19.2. Статика ~ при условии (1)

Преобразуем, используя (2):

Ясно, что~N(0,1)  по теореме Пирсона  ~.

Утверждение 19.3. Статика ~

Преобразуем с помощью (3):

(4)

Если обозначить , то очевидно, что ~N(0,1) для любого k.

Другое представление для :

=

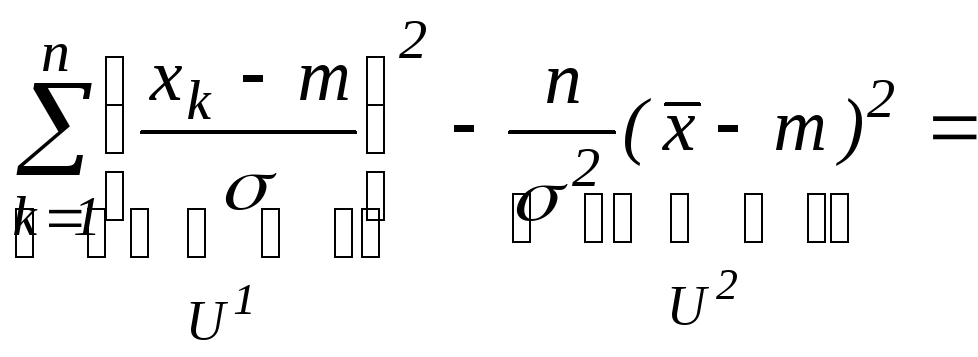
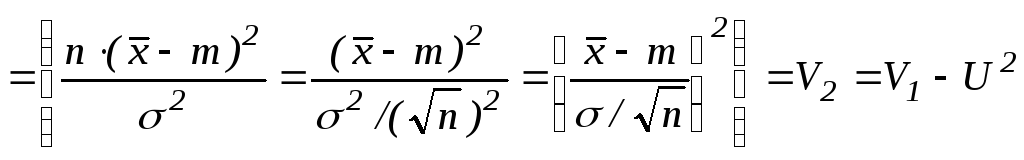(5)

Уравнение перепишем в виде: (6)

Известно, что ~, ~.

В теореме Филера доказывается, что и независимы (с помощью ортогональных преобразований).

Положим, ~, k – неизвестно.

Так как композиционно устойчиво,то из (6)  n=k+1  k=n-1  ~.

Утверждение 19.3. Статика ~St(n-1).

Преобразуем W:

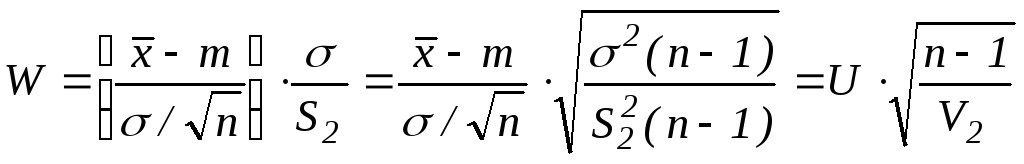, где U и V₂­ – независимы  по теореме Стьюдента  W~St(n-1).

 6.4.3. Понятие доверительного интервала и методика его построения.

Пусть  - неизвестная характеристика генерального,

- ее оценка по выборке;

( -) – ошибка при оценивании;

- абсолютная ошибка при этом,  - точность.

В статике  найти невозможно, но можно решить задачу о вероятности точности 

Подстановка правомерна: с какой вероятностью можно достичь заданной точности оценивания?

По заданному надо указать соответственную . (например

Простой пример. (оценка математического ожидания) Найти из условия

Известно, что ~N( , ).