Вопрос №12

Структура общего решения неоднородной системы уравнений

Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.

Рассмотрим неоднородную систему  и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений  и  неоднородной системы есть решение однородной системы.

Действительно, из равенств  и  следует, что .

2. Пусть  — решение неоднородной системы. Тогда любое решение  неоднородной системы можно представить в виде

, где  — решение однородной системы.

В самом деле, для любого решения  неоднородной системы разность  по свойству 1 является решением однородной системы, т.е.  — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть  — решение неоднородной системы, а  — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

(5.15)

при любых значениях [i]произвольных постоянных  является решением неоднородной системы, и, наоборот, для каждого решения  этой системы найдутся такие значения произвольных постоянных , при которых это решение  удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Алгоритм решения неоднородной системы уравнений

1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).

6. Найти частное решение  неоднородной системы, положив в (5.11) все свободные переменные равными нулю.

7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему  ее решений. Для этого подставить в (5.13) последовательно  стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.

8. Записать общее решение неоднородной системы по формуле (5.15).

Замечания 5.4

1. Используя фундаментальную матрицу  однородной системы , решение неоднородной системы  можно представить в виде

где  — частное решение неоднородной системы, а  — столбец произвольных постоянных.

2. Если базисный минор матрицы  расположен в левом верхнем углу (в первых  строках и первых  столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы

Тогда блочная матрица  оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец  является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде

(5.16)

где  — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.

Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы

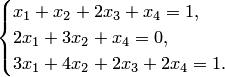
Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:

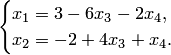
Переменные  — базисные, а  — свободные.

6. Полагая , получаем частное решение неоднородной системы .

7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):

8. Записываем по формуле (5.15) общее решение неоднородной системы

Искомая структура множества решений найдена.

Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:

Записываем частное решение неоднородной системы

и составляем фундаментальную матрицу:

По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):

которое совпадает с ранее полученным.

Метод вариации постоянных

Рассмотрим неоднородное уравнение -го порядка

,                                           (1)

где коэффициенты  и правая часть  - заданные непрерывные функции на интервале .

 

Допустим, что нам известна фундаментальная система решений  соответствующего однородного уравнения

                                       (2)

Как мы показали в § 1.15 (формула (6)), общее решение уравнения (1) равно сумме общего решения уравнения (2) и какого-либо решения уравнения (1).

Решение неоднородного уравнения (1) можно получить методом вариации постоянных, если известно общее решение однородного уравнения (2). Разъясним этот метод на примере уравнения порядка.

Итак, пусть задано линейное уравнение третьего порядка

.                                                        (3)

Пусть общее решение соответствующего однородного уравнения есть

,                             (4)

где  - линейно независимые решения уравнения (2)

.

Будем искать решение неоднородного уравнения (3) в виде суммы (4), где  - некоторые непрерывно дифференцируемые функции, которые надо найти. Наложим на искомые функции  два условия

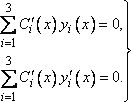                                                               (5)

Тогда будет

Подставив эти производные и саму функцию  в (3), получим

,

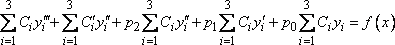или

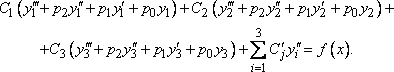
Но выражения в скобках в левой части этого равенства равны нулю, поэтому

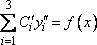.                                                                (6)

Мы получили уравнение (6) и два уравнения (5) с коэффициентами  и правой частью , которые непрерывны на . Эти три уравнения образуют линейную алгебраическую систему относительно неизвестных  с определителем, не равным нулю, потому, что это есть определитель Вронского для фундаментальной системы решений . Поэтому данная система имеет единственное решение

где  - непрерывные на  функции. Отсюда

.                                                      (7)

При этом функции  имеют на  непрерывную производную. Следовательно, частное решение неоднородного уравнения (1) имеет вид

,

где функции  определяются равенствами (7).

Пример,  - корни характеристического уравнения; общее решение однородного уравнения .

Найдем частное решение неоднородного уравнения методом вариации постоянных  и . Составим систему 5), (6):

.

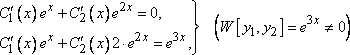Решая систему, имеем . Отсюда  и частное решение

.

Таким образом, общее решение исходного уравнения

Вопрос №13 Определения

Задача Коши, ,  - начальные данные:

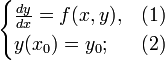
Решением задачи Коши является функция, определённая на интервале <a,b>, включающем , являющаяся решением уравнения (1) и удовлетворяющая начальному условию (2).

Определение. Решением интегрального уравнения:

является функция , которая определена на <a,b> и

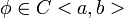1.  (непрерывна)

2.  <a,b>

3. подстановка 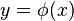 превращает уравнение (3) в тождество.

Лемма. Функция  является решением задачи Коши тогда и только тогда, когда она является решением интегрального уравнения.

Доказательство. Пусть  - решение задачи Коши  и 

Проинтегрируем тождество от  до :

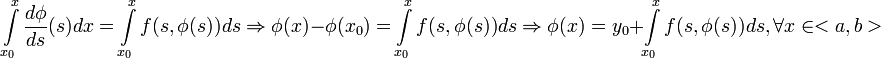
Теперь пусть  - решение интегрального уравнения, покажем, что она есть решение дифф. уравнения и удовлетворяет начальному условию. Для этого вначале подставим в (3) : 

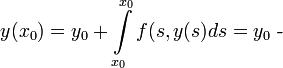
Продифференцируем (3) и получим (1)

Определение. , заданная на , удовлетворяет условию Липшица, если 

Заметим, что если функция удовлетворяет условию Липшица, то она является равномерно непрерывной на  (для док-ва замечания надо взять )

Определение. Последовательность функций  является равномерно ограниченной если 

Определение. Последовательность функций  называется равнестепенно непрерывной, если