Лекции / 6

6. Метод моментов для точной оценки параметров распределения. Примеры.

Метод моментов заключается в приравнивании теорет. моментов к соотв. эмпирическим моментам того же порядка. Он основывается на том факте, что эмп. ф-я распределения при достат. большом числе наблюд-й мало отлич. от теор. Сл-но, выборочные моменты явл. асимптотически несмещенными и состоятельными оценками теоретических моментов. В рез-те применения этого метода получ. сист. уравн-й. При числе ур-й больших 4-ех этот метод не дает точн. оценки. Если распределение характериз. одним параметром, то для его отыскания приравнивают один теор. момент к одному эмпир. моменту. Например, можно приравнять нач-е моменты 1-го порядка, т.е. . Для генер. совокупности . Более подробно

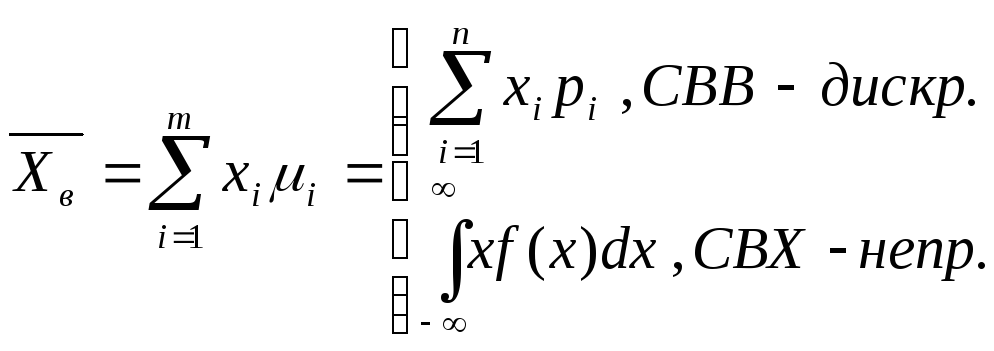
Как видно из последнего соотношения МО явл. функцией неизв. параметра. Поэтому решив ур-е (1), получим его точечн. оценку. Если распред-е хар-ся 2-мя параметрами, то надо приравнять 2 момента, напр., нач. момент 1-го порядка и центр. момент 2-го порядка. В рез-те получим сист.. Но оценки, получ. методом моментов не однозначны, т.к. можно приравнять как центр., так и нач моменты.

Пример: СВ Х распред. по з. Пуассона: , где m – число испытаний в одном опыте, - число появлений события в i-м опыте. Найти методом моментов по выборке оценку неизв. параметра . Воспользуемся ур-м (1). Как изв, для р. Пуассона , т.е. выборочное среднее - оценка параметра.