Лекции / 25

Вопрос 25.Свойства оценок наименьших квадратов. Ортогональная матрица планов.

1. Если распределение -нормальное, то оценка является наилучшей несмещенной оценкой для (в классе всех несмещенных оценок, т. е. и любая другая оценка ’) . имеет большую чем дисперсию. Оценка , являющаяся при этом оценкой максимального правдоподобия для , эффективная оценка для .

2. Если , , i=1,2,… и ковариация , то свойство (1) также будет иметь место и в случае, распределение не является нормальным. Действительно, =

Теорема. Пусть - оценка наименьших квадратов для , тогда в классе всех линейных оценок линейной комбинации , где - это вектор-строка, у которого j-ый элемент равен 1, а все остальные равны 0. Оценка является единственной оценкой обладающей минимальной дисперсией.

Эта теорема остаётся в силе и тогда, когда ранг матрицы X меньше k. В общем случае МНК оценки теряют оптимальные свойства. Когда общее для всех распределение не является нормальным, оценка наименьших квадратов для не совпадает с асимптотической эффективной оценкой максимального правдоподобия, но является асимптотически эффективной.

Ортогональные матрицы плана.

Если матрицу Х можно разбить на m совокупность столбцов так, чтобы для всех ij столбцы матрицы были ортогональны столбцам матрицы , т. е. матрицу

=0, при ij , то матрицу плана наз. ортогональной.

Разобьем соотв. образом и значение .

Пусть -это ранг матрицы , причем , где k-ранг матрицы .

Из равенства с учетом =0, при ij получаем

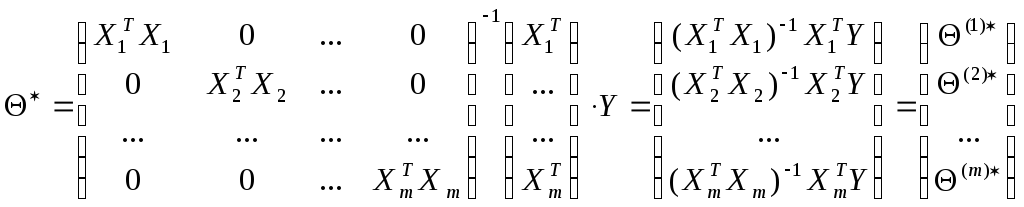
Это означает, что в случае ортогональной матрицы плана МНК (метод наименьших квадратов) оценки каждого столбца не зависимы друг от друга и не изменяются, если какие-либо из них положить =0.

Остаточная сумма квадратов в этом случае имеет вид:

.

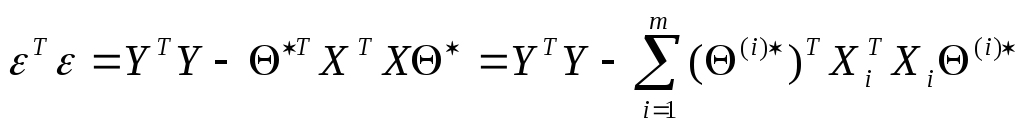Если про какие-то значения известно, что они =0, то величина остаточной суммы квадратов будет больше.

Т. к. эти величины независимые между собой целесообразна независимая проверка гипотез рав-ва 0 каждой из этих оценок.

Это свойство широко используется в дисперсионном анализе.