- •Тема 1. Второй закон термодинамики.
- •94. Определите изменение энтропии для реакции
- •Решение.
- •Решение.
- •121. Рассчитайте давления, при которых графит и алмаз находятся в равновесии для интервала температур 298—4000 к. При расчете используйте следующие данные для равновесия с (графит) с (алмаз):
- •Решение.
- •Решение.
- •Многовариантные задачи
- •Решение.
- •Тема 2. Характеристические функции
- •Решение:
- •Решение.
- •Решение.
- •Решение.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. А.А. КУЛЕШОВА»
А.В. Клебанов
М.А. Бандюк
РЕШЕБНИК ПО ФИЗИЧЕСКОЙ ХИМИИ.
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Методическая разработка
МОГИЛЕВ 2012
СОДЕРЖАНИЕ
-
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ..ИЗМЕНЕНИЕ ЭНТРОПИИ………………………………………………..3
-
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ……………………………………………….105
Тема 1. Второй закон термодинамики.
ИЗМЕНЕНИЕ ЭНТРОПИИ
1. Энтальпия плавления льда при 00С равна 6012 Дж/моль. Чему равна энтропия плавления льда? Найти энтропию льда при 00С, если энтропия воды при этой температуре равна 63,34 Дж/моль∙К.
Решение.
ΔSпл.= =22,01
=22,01
ΔSльда=ΔSводы-ΔSпл.=63,34-22,01=41,33 Дж/моль∙К
Ответ: 41,33 Дж/моль∙К
2. Энторопия жидкого ацетона при температуре кипения 56,20С равна 213,31 Дж/моль∙К. Энтальпия испарения ацетона 29090 Дж/моль. Найти энтропию парообразного ацетона при температуре 56,20С и давлении 1 атм.
Решение.
ΔSисп.=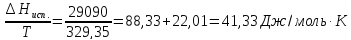
Ответ: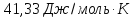
3. Диоксид углерода CO2 сублимирует при температуре -78,50С и давлении 1 атм. Энтальпия сублимации 25230 Дж/моль. Чему равна энтропия сублимации?
Решение.
ΔSсубл.=
Ответ: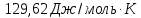
4. Серое олово при температуре 130С обратимо превращается в белое олова. Энтальпия превращения 20,92 Дж/моль. Чему равна энтропия превращения?
Решение.
ΔSпревр.=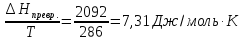
Ответ:
5. При температуре 95,50С и давлении 1 атм. Ромбическая сера обратимо превращается в моноклинную. Энтальпия превращения 450 Дж/моль. Чему равна энтропия моноклинной серы, если энтропия ромбической серы при этой температуре 36,73 Дж/моль∙К
Решение.
ΔSпревр.=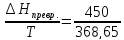 =1,22 Дж/моль∙К
=1,22 Дж/моль∙К
Ответ: 1,22 Дж/моль∙К
6. Молярная энтропия водорода при 250С и 1 атм. Равна 130,62 Дж/моль∙К. Чему равна энтропия водорода при 1000С и 1 атм. , если теплоёмкость Ср(г)=28,85 Дж/моль∙К?
Решение.
ΔS=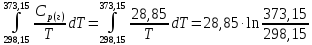 =
6,47 Дж/моль∙К
=
6,47 Дж/моль∙К
ΔS1000C= ΔS250C+ ΔS=130,52+6,47=136,99 Дж/моль∙К
Ответ: 136,99 Дж/моль∙К
7.
Энтропия CO
при 25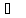 и 1атм. равна 197,55 Дж/моль∙К. Чему равна
энтропия CO
при 200
и 1атм. равна 197,55 Дж/моль∙К. Чему равна
энтропия CO
при 200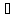 и 50 атм., предполагая, что CO
является идеальным газом?
и 50 атм., предполагая, что CO
является идеальным газом?
Решение.
ΔS=Cvln Дж/моль∙К
Дж/моль∙К
ΔS200= ΔS+ ΔS25=9,59+197,55=207,1 Дж/моль∙К
Ответ: 207,1 Дж/моль∙К
8.
Один моля кислорода расширяется до
десятикратного увеличения объёма и
одновременно охлаждается от 127 до 27 Чему равно изменение энтропии, если
теплоёмкость Ср(г)=29,2
Дж/моль∙К
Чему равно изменение энтропии, если
теплоёмкость Ср(г)=29,2
Дж/моль∙К
Решение:
ΔS=Cрln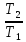 =29,2ln
=29,2ln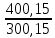 =8,39
Дж/моль∙К
=8,39
Дж/моль∙К
Ответ: 8,39 Дж/моль∙К
9.
Энтропия NH3
при 25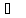 и 1 атм. равна 192,66 Дж/моль∙К. Зависимость
теплоёмкости Ср
от температуры выражается уравнением:
Ср(г)=
29,80+25,48∙10-3T-1,67∙105T-2
Дж/моль∙К.
Чему равна энтропия аммиака при 500
и 1 атм. равна 192,66 Дж/моль∙К. Зависимость
теплоёмкости Ср
от температуры выражается уравнением:
Ср(г)=
29,80+25,48∙10-3T-1,67∙105T-2
Дж/моль∙К.
Чему равна энтропия аммиака при 500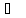 и 10 атм.?
и 10 атм.?
Решение.
ΔS=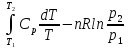 =29,80∙ln
=29,80∙ln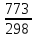 +25,48∙
+25,48∙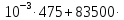 (1,67
(1,67 )=39,699
)=39,699
ΔS=39,699-8,314∙ln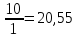
ΔS500= ΔS+ ΔS25=20,55+192,66=213,21
Ответ: 213,21 Дж/моль∙К
10. Найти изменение энтропии при переходе двух молей кислорода от объёма 30 л под давлением 3 атм. к объёму 15 л под давлением2 атм. Считать кислород идеальным газом.
Решение.
ΔS=n
( Cp
ln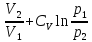 )=2(
)=2( )=-23,49
)=-23,49
Ответ: -23,49 Дж/моль∙К
11. Один моль идеального газа, занимающий объём 26 л, подвергается изотермическому расширению. Изменение энтропии 40 Дж/моль∙К. Каков конечный объём газа?
Решение:
ΔS=R
ln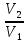
40=8,314ln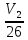
ln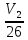 =4,81
=4,81
V2=3191 л
Ответ: 3191 л
12.
11,2 л азота нагревают от 0 до 100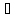 и одновременно уменьшают давление от
1 до 0,01 атм. Найти изменение энтропии,
считая азот идеальным газом.
и одновременно уменьшают давление от
1 до 0,01 атм. Найти изменение энтропии,
считая азот идеальным газом.
Решение.
ΔS=n
( Cp
ln )
)
n(N2)= =0,5
моль
=0,5
моль
ΔS=0,5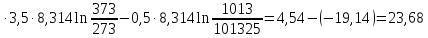
Ответ: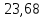 Дж/моль∙К
Дж/моль∙К
13.
Один моль двухатомного идеального газа
находится при 200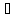 и 5 атм. В результате нагревания и сжатия
газа температура стала 500
и 5 атм. В результате нагревания и сжатия
газа температура стала 500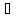 ,
давление равно 10 атм. Найти изменение
энтропии газа.
,
давление равно 10 атм. Найти изменение
энтропии газа.
Решение.
ΔS=nCp
ln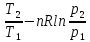
ΔS=3,5∙8,314ln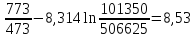
Ответ: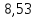 Дж/моль∙К
Дж/моль∙К
14.
Вычислить изменение энтропии при
нагревании одного моля CdS
от -120
до 0°С, если
зависимость мольной теплоемкости от
температуры выражается уравнением
Ср=54,0+3,8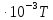 ,Дж/моль∙К
,Дж/моль∙К
Решение.
Изменение энтропии рассчитывается по формуле

Ответ:
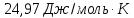
15. При
охлаждении 12 л кислорода от 200 до -40 °С
давление повышается от
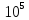 до 6,0
до 6,0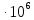 H/
H/ .
Рассчитать изменение энтропии, если
.
Рассчитать изменение энтропии, если
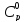 = 29,2
Дж/моль
= 29,2
Дж/моль К
(считать кислород идеальным газом).
К
(считать кислород идеальным газом).
Решение.
Находим число молей кислорода из уравнения состояния идеального газа:
n=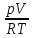 =
=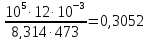
Поскольку в процессе меняется и давление и температура,
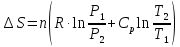
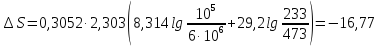 Дж/моль∙К
Дж/моль∙К
Ответ:
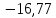 Дж/моль∙К
Дж/моль∙К
16. Определить изменение энтропии при превращении 2 г воды в пар при изменении температуры от 0 до 150°С и давлении I ат, если скрытая удельная теплота парообразования воды 2,255 кДж/г, мольная теплоемкость пара при постоянном давлении
Ср=30,13+11,3 103Т,
Дж/моль
103Т,
Дж/моль К.
К.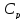 жидкой воды
75,30 Дж/моль
жидкой воды
75,30 Дж/моль К
К
Решение. Общее изменение энтропии складывается из трех составляющих:
1) нагревание жидкой воды от 0 до 100°С;
2) переход жидкой воды в пар при 100°С;
3) нагревание водяного пара от 100 до 150°С.
Для первой стадии изменение энтропии рассчитывается по формуле

где n - количество молей воды. Учитывая, что Ср является постоянной
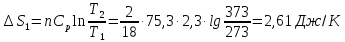
Изменение энтропии на второй стадии определяется но формуле
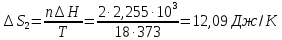
Изменение энтропии
на третьей стадии рассчитывается
по формуле

Общее изменение энтропии равно:

Ответ:

17. Найти изменение энтропии при нагревании 1 моля кадмия от 25 до 7270С, если температура плавления 3210С и энтальпия плавления 6109 Дж/моль. Теплоёмкость кристаллического и жидкого кадмия Ср(кр)=22,22+0,0123T Дж/моль∙К, Ср(ж)=29,83 Дж/моль∙К
Решение.
25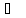 727
727

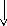
 Cd(тв.) Cd(тв.)
Cd(тв.) Cd(тв.)
S1 S3
 Cd(ж.)
Cd(ж.)
Cd(ж.)
Cd(ж.)
321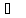 S2
321
S2
321
ΔS1=22,22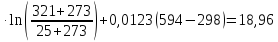
ΔS2=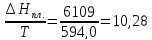
ΔS3=29,83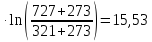
ΔS= ΔS1+ ΔS2+ ΔS3=18,96-10,28+15,53=44,78 Дж/моль∙К
Ответ: 44,78 Дж/моль∙К
18.
Энтропия кристаллического хлорида
натрия равна 72,13 Дж/моль∙К при Т=298,15 К
и Р=1 атм. Найти энтропию расплавленной
соли при температуре 850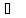 ,
если температура плавления 800
,
если температура плавления 800 а
энтальпия плавления 31,0 Дж/моль∙К.
Теплоёмкость NaCl
в твёрдом и жидком состоянии равна:
а
энтальпия плавления 31,0 Дж/моль∙К.
Теплоёмкость NaCl
в твёрдом и жидком состоянии равна:
Ср(кр)= 49,94+16,32∙10-3T Дж/моль∙К
Ср(ж)=66,53 Дж/моль∙К
Решение.
298,150K 8500С
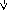
 NaCl
(кр) NaCl(расп.)
NaCl
(кр) NaCl(расп.)
 NaCl(пл.)
NaCl(пл.)
NaCl(пл.)
NaCl(пл.)
8000С 8000С
ΔS1=49,94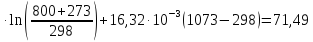 Дж/моль ∙К
Дж/моль ∙К
ΔS2=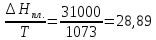 Дж/моль ∙К
Дж/моль ∙К
ΔS3=66,53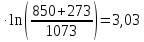 Дж/моль∙К
Дж/моль∙К
ΔS850=ΔSNaCl+ ΔS1+ ΔS2+ ΔS3=72,13+71,49+28,89+3,03=175,53 Дж/моль∙К
Ответ: 175,53 Дж/моль∙К
19.
Вычислите изменение энтропии при
нагревании 1 моля твёрдого брома от
температуры плавления -7,32 до 100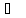 ,
если энтальпия плавления 10544 Дж/моль,
энтальпия испарения 30710 Дж/моль,
температура кипения 59
,
если энтальпия плавления 10544 Дж/моль,
энтальпия испарения 30710 Дж/моль,
температура кипения 59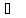 .
Теплоёмкость брома в жидком и парообразном
состоянии равна:
.
Теплоёмкость брома в жидком и парообразном
состоянии равна:
Ср(ж)= 75,71 Дж/моль∙К
Ср(г)= 37,20+0,71∙10-3T-1,19∙105T-2Дж/моль∙К
Решение.
265,60K 2730K
 Br(ж.)
Br(тв.)
Br(ж.)
Br(тв.)
 Br(ж.)
Br(тв.)
Br(ж.)
Br(тв.)
3320K 3320K
ΔSпл.=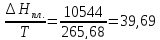 Дж/моль∙К
Дж/моль∙К
ΔS1=75,71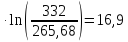
ΔS2=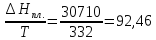 Дж/моль∙К
Дж/моль∙К
ΔS3=37,20
ΔS=16,91+92,46+4,135=113,51 Дж/моль∙К
Ответ: 113,51 Дж/моль∙К
20.
Энтропия жидкого бензола при 25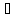 и 1 атм. равна 173,26 Дж/моль∙К. Найти
энтропию газообразного бензола при
500
и 1 атм. равна 173,26 Дж/моль∙К. Найти
энтропию газообразного бензола при
500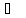 и 1 атм. , если энтальпия испарения бензола
при температуре кипения 80,1
и 1 атм. , если энтальпия испарения бензола
при температуре кипения 80,1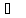 равна 30752 Дж/моль. Теплоёмкость жидкого
и газообразного бензола выражается
уравнениями:
равна 30752 Дж/моль. Теплоёмкость жидкого
и газообразного бензола выражается
уравнениями:
Ср(ж)= 59,50+255,0 ∙10-3T Дж/моль∙К
Ср(г)= -21,09+400,1∙10-3T-169,9∙10-6T-2 Дж/моль∙К
Решение.
ΔSисп.(500)=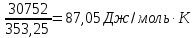
ΔS(ж)=59,50∙
ln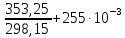 ∙(353,25-298,15)=24,16
∙(353,25-298,15)=24,16
ΔS(г)=
-21б09∙ ln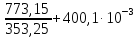 ∙(773,15-353,25)-
∙(773,15-353,25)-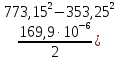 =111,282
=111,282
ΔS=173,26+87,05+24,16+111,282=395,752 Дж/моль∙ К
Ответ: 395,752 Дж/моль∙ К
21.
Вычислить
изменение энтропии системы и окружающей
среды при изотермическом затвердевании
1 моля меди, переохлаждённой ниже
температуры плавления на 180 градусов.
Температура плавления меди 1356 К, энтальпия
плавления Δпл.H1356
K=12970
Дж/моль. Теплоёмкость твердой и жидкой
меди: Ср=22.64+6,28∙ ,
Дж/моль∙ К
,
Дж/моль∙ К
Ср= 31,38 Дж/моль∙ К
Решение.
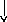

 1176
K
Cu(ж) Cu(кр)
1176
K
Cu(ж) Cu(кр)
 1356
Cu(ж) Cu(кр)
1356
Cu(ж) Cu(кр)
T=1082,85-180=902,85 =1176
K
=1176
K
ΔS1=31,38
ln
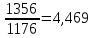 Дж/моль∙ К
Дж/моль∙ К
ΔS2=-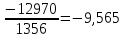 Дж/моль∙ К
Дж/моль∙ К
ΔS3=22,64
ln
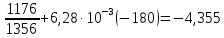 Дж/моль∙ К
Дж/моль∙ К
ΔSобщ= ΔS1+ ΔS2+ ΔS3=4,469+(-9,565)+(-4,355)=-9,45 Дж/моль∙ К
ΔSсреда=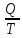
Q=-12970+((22,64∙(-180)+3,14∙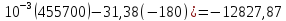
ΔSсреда=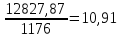
ΔSобщ=10,91-9,45=1,46 Дж/моль∙ К
Ответ: 1,46 Дж/моль∙ К
22.
Рассчитать разность между мольными
энтропиями твёрдой и жидкой ртути при
температуре -50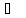 .
Температура плавления ртути -39
.
Температура плавления ртути -39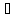 ,
энтальпия плавления при этой температуре
2340 Дж/моль. Теплоёмкость жидкой и твёрдой
ртути равна: Ср(кр)=29,71+6,69∙
,
энтальпия плавления при этой температуре
2340 Дж/моль. Теплоёмкость жидкой и твёрдой
ртути равна: Ср(кр)=29,71+6,69∙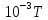 ,
Дж/моль∙ К
,
Дж/моль∙ К
Ср(ж)= 26,9 Дж/моль∙ К
Решение.
ΔS1=26,9
ln
 Дж/моль∙ К
Дж/моль∙ К
ΔS2=-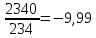 Дж/моль∙ К
Дж/моль∙ К
ΔS3=29,71
ln
 Дж/моль∙ К
Дж/моль∙ К
ΔS=-1,5-9,99+1,29=-10,20 Дж/моль∙ К
Ответ: -10,20 Дж/моль∙ К
23.
Два сосуда объёмом 1 л каждый соединены
трубкой с краном. В одном находится
водород при 1 атм. и 20 ,
в другом – гелий при 3 атм. и 100
,
в другом – гелий при 3 атм. и 100 . Найти изменение энтропии системы
после открытия крана и достижения
равновесной температуры, если стенки
сосудов и трубки теплоизолированные
от окружающей среды, Газы считать
идеальными.
. Найти изменение энтропии системы
после открытия крана и достижения
равновесной температуры, если стенки
сосудов и трубки теплоизолированные
от окружающей среды, Газы считать
идеальными.
Решение.

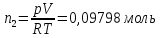
ΔS=nRln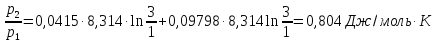
Ответ: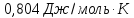
24. Вычислите изменение энтропии при плавлении 5 молей бензола, если температура плавления бензола равна 278.68 К, а теплота плавления 2,351 ккал/моль.
Решение.
Плавление бензола
- фазовый переход, протекающий при
постоянной температуре. Изменение
энтропии при переходе 5 молей
вещества из
твердого в жидкое состояние определим,
используя формулу
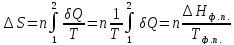

Ответ:
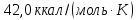
25.
Определите изменение энтропии при
превращении 2 г
воды в пар при
изменении температуры от 0 до 100
 и давлении 1 атм.,
если скрытая
удельная теплота парообразования воды
равна 2,255 кДж/г.
Мольная
изобарическая
теплоемкость жидкой воды в рассматриваемом
температурном интервале постоянна и
равна 75,30Дж/(моль
К).
и давлении 1 атм.,
если скрытая
удельная теплота парообразования воды
равна 2,255 кДж/г.
Мольная
изобарическая
теплоемкость жидкой воды в рассматриваемом
температурном интервале постоянна и
равна 75,30Дж/(моль
К).
Решение.
Изменение энтропии
системы в рассматриваемом температурном
интервале происходит в результате
течения следующих процессов: а) нагревания
воды от 0
 до
100
до
100
 в изобарических
условиях; б) испарения воды при температуре
кипения в изотермических условиях.
Следовательно, суммарное изменение
энтропии AS
равно сумме
изменений энтропии в процессах а) и б):
в изобарических
условиях; б) испарения воды при температуре
кипения в изотермических условиях.
Следовательно, суммарное изменение
энтропии AS
равно сумме
изменений энтропии в процессах а) и б):
А)
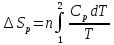
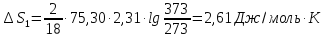
Б)
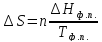 или
или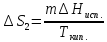
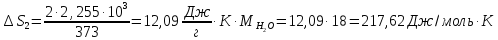

Ответ: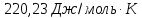
26.
Определите изменение энтропии при
нагреве I
моля Аl
от 25 до 600
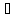 ,
если для него
в этом интервале теплоёмкость зависит
от температуры следующим образом: Ср
= 20,945 + 0,010728Т.
(Дж/(моль К)).
,
если для него
в этом интервале теплоёмкость зависит
от температуры следующим образом: Ср
= 20,945 + 0,010728Т.
(Дж/(моль К)).
Решение.
Для нагревания вещества при постоянном давлении:
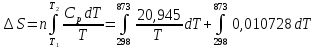

Ответ:
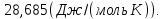
27. Определите изменение энтропии при плавлении меди массой 63,5 г, если теплота плавления меди равна 12980 Дж/моль. а температура плавления меди 1083 °С.
Решение.
n(Сu)=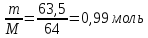
ΔS=n
Ответ: 9,57 Дж
28. Вычислите изменение энтропии при плавлении свинца массой 100 г, если температура плавления свинца 327,4 °С, а теплота плавления 5485 Дж/моль.
Решение.
m(Pb)=100 г
Tпл=327,4
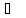
Qпл=5485 Дж/моль
n(Pb)=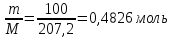
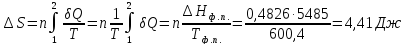
Ответ:
29. В двух сосудах одинаковой вместимости находится: в первом - азот массой 2,8 г, во втором аргон массой 4 г. Определите изменение энтропии при диффузии, возникающей в результате соединения сосудов с газами. Температура и давление постоянны.
Решение.
n(Ar)=
n(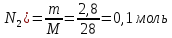
ΔS=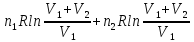 =0,1
=0,1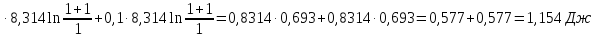
Ответ: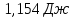
30.
Найдите изменение энтропии в процессе
обратимого изотермического сжатия 1
моля кислорода от 1,013
 105до
10,13
105до
10,13 105Па.
105Па.
Решение.
ΔS=nRln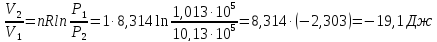
Ответ: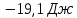
31.
Вода массой 100 г при 25 °С превращена в
пар с температурой 150 °С и давлением
1,013 105
Па. Вычислите изменение энтропии этого
перехода, если удельная теплота испарения
воды при 100
105
Па. Вычислите изменение энтропии этого
перехода, если удельная теплота испарения
воды при 100 равна 2257 Дж/ г, удельная теплоемкость
воды - 4,187 Дж/(г
равна 2257 Дж/ г, удельная теплоемкость
воды - 4,187 Дж/(г К),
а удельная теплоемкость водяного пара
при давлении 1,013
К),
а удельная теплоемкость водяного пара
при давлении 1,013
 105
Па равна 1,968 Дж/(г
105
Па равна 1,968 Дж/(г К).
К).
Решение.
Δ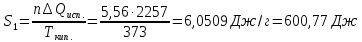
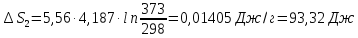
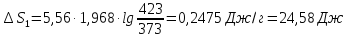
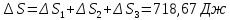
Ответ: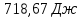
32.
Найдите изменение энтропии при переходе
3 молей кислорода от объема 0,0336 м3
под давлением 2,026 105
Па к объему 0,0672 м3
под давлением 1,013
105
Па к объему 0,0672 м3
под давлением 1,013 105
Па. Молярная теплоемкость кислорода
Ср
равна 29,37 Дж/(моль
105
Па. Молярная теплоемкость кислорода
Ср
равна 29,37 Дж/(моль К),
температура постоянна.
К),
температура постоянна.
Решение.
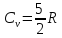 =20,785
=20,785
ΔS=n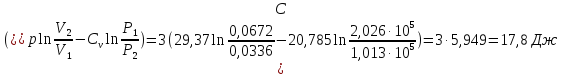
Ответ:

33.
Определите разность энтропии 1г воды
при 0 и 100
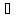 (давление нормальное), считая теплоемкость
воды постоянной и равной 4,19 Дж/(г
(давление нормальное), считая теплоемкость
воды постоянной и равной 4,19 Дж/(г К).
К).
Решение.
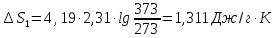
Ответ:
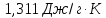
34. Определите изменение энтропии при охлаждении 5 молей алюминия от 0 до -100 °С. Средняя массовая
теплоемкость
алюминия в указанном интервале
температур 0,8129 Дж/(г К).
К).
Решение.

Ответ:
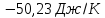
35.
Чему равно изменение энтропии 1 моля
нафталина при нагревании от 0 до 80,4 °С
(температура плавления), если теплота
плавления 149,6 Дж/г, а средняя массовая
теплоемкость кристаллического нафталина
1,315 Дж/(г К).
К).
Решение.
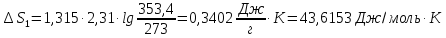
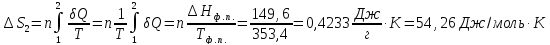
ΔS=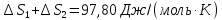
Ответ:
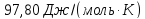
36.
Рассчитайте суммарное изменение энтропии
при нагревании 1 моля бензола от
температуры плавления (5,49 °С) до полного
испарения при температуре кипения (80,2
°С). Теплота плавления бензола 126,54 Дж/г,
теплота парообразования 396 Дж/г, массовая
теплоемкость бензола 1,94 Дж/(г К).
К).
Решение.
ΔS=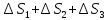
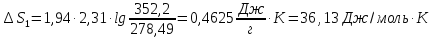
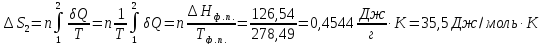
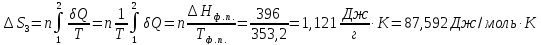
ΔS=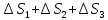 =159,2
Дж/(моль
=159,2
Дж/(моль К)\
К)\
Ответ:
159,2 Дж/(моль К)
К)
37.
В 0,30 кг жидкого
ацетона поместили серебряную ложку
массой 53 г. Определите энтропию системы
при 25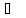 .
.
Решение.
Находим значения стандартных энтропий: для жидкого ацетона
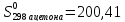 Дж/моль ∙К и для
серебра
Дж/моль ∙К и для
серебра
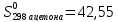 Дж/моль ∙К. Молярные массы равны:
ацетона-0,058 и серебра-0,108 кг/моль.
Дж/моль ∙К. Молярные массы равны:
ацетона-0,058 и серебра-0,108 кг/моль.
По полученным данным:
Энтропия 0,30 кг ацетона-
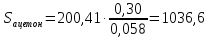 Дж/К
Дж/К
Энтропия серебряной ложки-
 Дж/К
Дж/К
Отсюда энтропия всей системы:
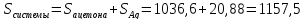 Дж/К
Дж/К
Ответ:
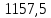 Дж/К
Дж/К
38.
Вычислите
изменение энтропии в процессе затвердения
1 моль переохлажденного бензола при 268
К, если при 278 К
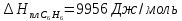 ,
,
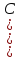 ,
,
,
,
 ,
P=const=1,01∙
,
P=const=1,01∙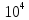 Па
Па
Решение.
Этот процесс необратим, поэтому мысленно проводим его обратимо в три стадии
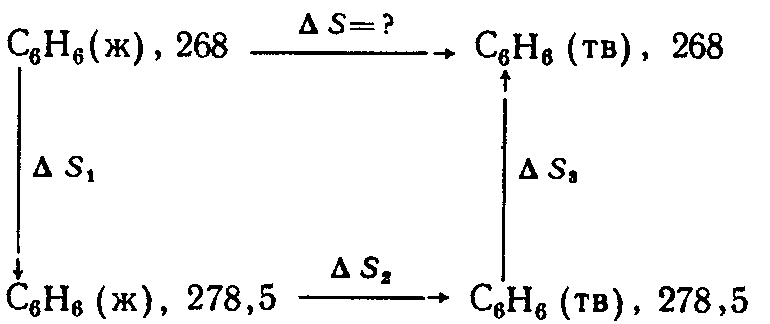
Тогда
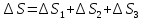
Вычисляем
 и
и
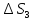 по уравнению (VII,5),
а
по уравнению (VII,5),
а
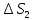 -по уравнению (VII.14).
Тогда
-по уравнению (VII.14).
Тогда
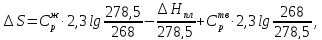
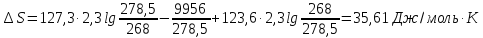
Ответ: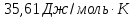
39. Вычислить энтропию хлорид серебра при 870 К.
Решение.
Согласно уравнению (VII. 15)
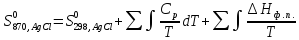
Выписываем из
справочника необходимые данные
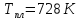 ,
,
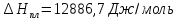 ,
,
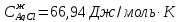 ,
,
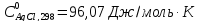 ,
, .
Подставляем
числа в уравнение
.
Подставляем
числа в уравнение
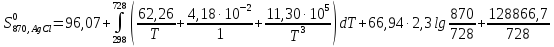
После интегрирования получаем

Приращение энтропии AgCl за счёт нагревания составит
( и
и
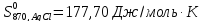
Ответ: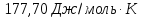
40. В одном из сосудов одинаковой вместимости 3 м3 находится 28 кг азота, а в другом 32 кг кислорода при одной и той же температуре. Вычислите изменение энтропии при диффузии в результате соприкосновения содержимого этих сосудов. Принять кислород и азот идеальными газами.
Решение.
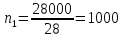 моль
моль
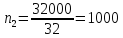 моль
моль
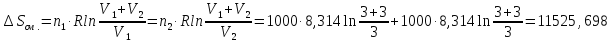 Дж/моль
Дж/моль
Ответ:
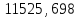 Дж/моль
Дж/моль
41. Определите ΔS для изобарического нагревания 1 моля азота от 300 до 10000 К. Ср = 6,4492 + 1,4125 · 10-3 Т – 0,807 · 10-7 Т2.
Решение.
ΔS=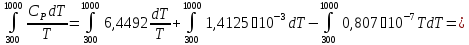
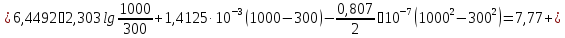
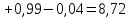 кал·0К-1·моль-1.
кал·0К-1·моль-1.
Ответ: кал·0К-1·моль-1.
кал·0К-1·моль-1.
42.
Нормальная температура кипения бензола
равно
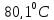 .
Оцените мольную теплоту испарения
бензола при этой температуре.
.
Оцените мольную теплоту испарения
бензола при этой температуре.
Решение.
Используя правило
Трутона ΔН пар
/Ткип≈21 ,
получим
ΔНпар≈Ткип·21=353·21=7400
,
получим
ΔНпар≈Ткип·21=353·21=7400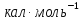
Экспериментально
значение равно 7220 кал.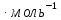
Ответ:
7400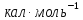
43. Найти изменение энтропии при превращении двух молей льда, взятых при О°С р = 1 атм, в пар при 200 °С и 3 атм. Теплота плавления льда равна 332,2 Дж∙г-1, теплота парообразования при 100 °С равна 2259 Дж∙г-1. Удельная теплоемкость пара равна 1,87 Дж∙г-1 ∙К-1, воды - 4,184 Дж∙г-1 ∙К-1 .
Решение.
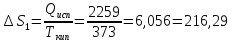 Дж∙К-1
Дж∙К-1
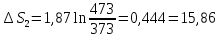 Дж∙К-1
Дж∙К-1
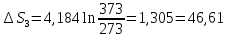 Дж∙К-1
Дж∙К-1
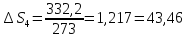 Дж∙К-1
Дж∙К-1
 Дж∙К-1
Дж∙К-1
Ответ:
 S=
306,32 Дж∙К-1.
S=
306,32 Дж∙К-1.
44. В одном из сосудов емкостью 0,1м3 находится кислород, в другом емкостью 0.4 м3 .В обоих сосудах температура 17е С и давление 1,013∙105 н/м2. Найти изменение энтропии при взаимной диффузии газов из одного сосуда в другой при Р и Т=const. Считать оба газа идеальными.
Решение.
Изменение энтропии определяем по формуле. Число молей каждого газа находим из уравнения Менделеева — Клапейрона
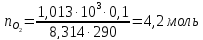
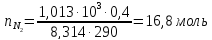
ΔS=2,3∙8,314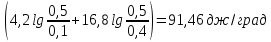
Ответ: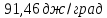
45.
Вычислить изменение энтропии в
процессе
изотермного расширения 2 моль
метана от
 =101,3∙
=101,3∙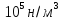 до
до
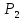 =1,013∙
=1,013∙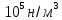 Газ
считать идеальным.
Газ
считать идеальным.
Решение.
По формуле (111,6) при Т=const находим
ΔS=-2∙8,314∙2,3lg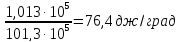
Ответ: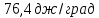
46. Рассчитать мольную энтропию окиси углерода при 200° С и 50,67∙105 н/м2, если энтропия при 25° С и 1,013∙105 н/м2 равна 197,9 дж/град∙моль, а зависимость мольной теплоемкости от температуры выражается уравнением
СР = 28,41+4,10∙10-3T — 0,46∙105T2 дж/моль∙ град.
Решение.
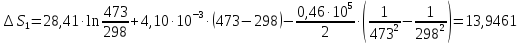
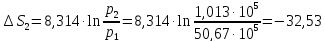
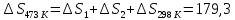 Дж/моль∙К
Дж/моль∙К
Ответ: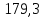 Дж/моль∙К
Дж/моль∙К
47. Найти изменение энтропии при нагревании I г∙атом кадмия от 25 до 727°С, если температура плавления 321°С и теплота плавления равна 6109 дж/г∙атом
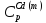 =
22,22+ 12,30∙
=
22,22+ 12,30∙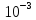 T
дж/моль∙град;
T
дж/моль∙град;
 =
= 29,83 дж/моль∙град.
=
= 29,83 дж/моль∙град.
Решение.
ΔS1=22,22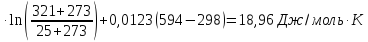
ΔS2=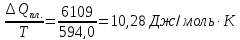
ΔS3=29,83
ΔS= ΔS1+ ΔS2+ ΔS3=18,96-10,28+15,53= 44,78 Дж/моль∙К
Ответ: 44,78 Дж/моль∙К
48. Какому конечному объему отвечает изменение энтропии, равное 38,28 дж/моль∙град, если 1 моль идеального газа, занимающий в данных условиях 0,02 м3, изотермически расширяется.
Решение.
ΔS=nRln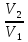
38,28=1∙8,314ln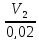
 л
л
Ответ: 2 м3
49.Насколько изменится энтропия в процессе изотермического расширения
10 г криптона от объема 0,05 м3 и давления 1,013∙105 н/м2 до объема 0,2 м3 и давления 0,2133∙105 н/м2 ?.
Решение.
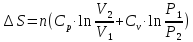
n(Kr)=0,1193 моль
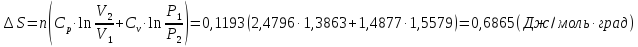
Ответ: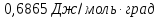
50. Найти изменение энтропии при изотермическом сжатии 1 моль паров бензола при 80°С от 0,4053∙105 до 1,013∙105 н/м2 с последующей конденсацией в охлаждением жидкого бензола до 60°С. Нормальная температура кипения бензола 80°С; мольная теплота испарения бензола 30,88 кдж/моль; удельная теплоемкость жидкого бензола 1,799 дж/г∙град.
Решение.
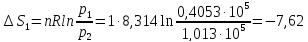 Дж/моль∙град
Дж/моль∙град
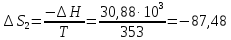 Дж/моль∙град
Дж/моль∙град
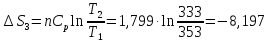 Дж/моль∙град
Дж/моль∙град
 Дж/моль∙град
Дж/моль∙град
Ответ: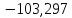 Дж/моль∙град
Дж/моль∙град
51. Определить
изменение энтропии в процессе сжижения
1 моль
метана, если
начальная температура равна 25°С, а
конечная 111,8° К. Мольная теплота испарения
метана при 111,8° К равна 8234,0 дж/моль
и мольная
теплоемкость
 =35,79
дж/моль∙град.
Вычислить
работу сжижения метана, приняв к. п.
д. равным 10%.
=35,79
дж/моль∙град.
Вычислить
работу сжижения метана, приняв к. п.
д. равным 10%.
Решение.
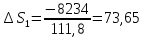 дж/моль∙град
дж/моль∙град
 дж/моль∙град
дж/моль∙град
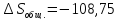 дж/моль∙град
дж/моль∙град
A=-143,11
Ответ:-108,75; -143,11
52. Рассчитать-изменение
энтропии 1 моль
бензола при
переходе из жидкого состояния при 25°С
в пар при 100°С, если теплота испарения
бензола 393,3 дж/г
и температура кипения бензола 80,2°С,
мольная теплоемкость жидкого бензола
равна Ср
(ж) = 136,1 дж/моль∙град,
а мольная
теплоемкость паров бензола
Ср(г) = - 33,90 +
471,87∙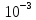 -298,34∙
-298,34∙ + 70,84∙
+ 70,84∙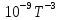 дж/моль∙град.
дж/моль∙град.
Решение.
Δ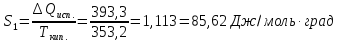
Δ
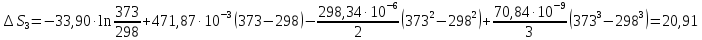
ΔS= Δ
Ответ: 107
53. Вычислить возрастание энтропии 1 моль брома Вr2. взятого при температуре плавления —7,32°С, и переходе его из твердого состояния в пар при температуре кипения 61,55°С; мольная теплоемкость жидкого брома
Ср(ж) = 0,4477 дж/г∙град; теплота плавления 67,72 дж/г; теплота испарения 182,8 дж/г.
Решение.
Δ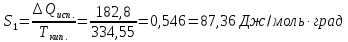
Δ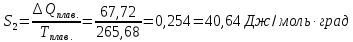
Δ
ΔS= Δ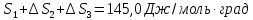
Ответ: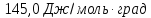
54. Определить увеличение энтропии 1 моля кристаллического магния при нагревании от 300 до 800 К при постоянном давлении, если теплоёмкость магния равна Ср(кр)= 22,3+10,64∙10-3T-0,42∙105T-2, Дж/моль∙К
Решение.
ΔS=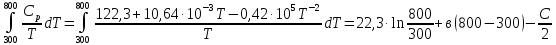 (
( -
-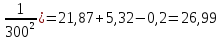 Дж/моль∙К
Дж/моль∙К
Ответ: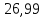 Дж/моль∙К
Дж/моль∙К
55. Определить увеличение энтропии 1 моля азота при нагревании от 25 до 10000С: а) при постоянном давлении; б) при постоянном объёме. Зависимость теплоёмкости от температуры выражается уравнением Ср=27,88+4,27∙10-3T Дж/моль∙К
Решение.
А)ΔS=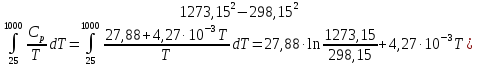 )=40,47+4,16325=44,64
Дж/моль∙К
)=40,47+4,16325=44,64
Дж/моль∙К
Б) Cp-Cv=R
Cv= Cp-R=27,88+4,27∙10-3T-8,314=19,566+4,27∙10-3T
ΔS=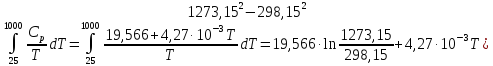 )=28,4+4,16325=32,56
Дж/моль∙К
)=28,4+4,16325=32,56
Дж/моль∙К
Ответ: 44,64 Дж/моль∙К; 32,56 Дж/моль∙К
56. Как изменится энтропия 1 моля гелия при нагревании его от 20 до 70 °С, если объем газа при этом изменится от 24 до 28,1 л?
Решение.
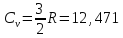
ΔS=n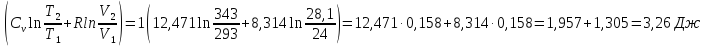
Ответ: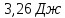
57.
Средняя массовая теплоемкость железа
в пределах температур 0 - 200 °С равна
0.486 Дж/(г К).
Определите изменение энтропии при
нагревании 1 кг железа oт
100 до 150 °С.
К).
Определите изменение энтропии при
нагревании 1 кг железа oт
100 до 150 °С.
Решение.
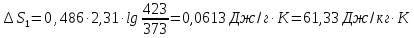
Ответ:
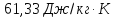
58.
Вычислите изменение энтропии при
нагревании 1 кг свинца от температуры
его плавления (327,4 °С) до 800
 .
Теплота
плавления свинца 24,8 кДж/кг, а теплоемкость
жидкого свинца в интервале температур
327 - 1000 °С равна
0,1415 кДж/(кг
.
Теплота
плавления свинца 24,8 кДж/кг, а теплоемкость
жидкого свинца в интервале температур
327 - 1000 °С равна
0,1415 кДж/(кг К).
К).
Решение.
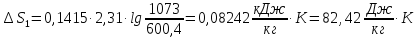
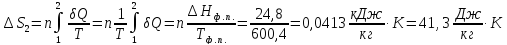
ΔS=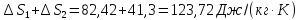
Ответ:
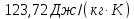
59. Вычислите изменение энтропии при нагревании 16кг О2 от 273 до 373К:
1) при постоянном объёме;
2) при постоянном давлении.
Считать кислород идеальным газом
Решение.
1) при постоянном объёме
n(О2)=16000/32=500 (моль)
ΔS=(5/2)∙n∙R∙ ln(T2/T1);
ΔS=5/2∙500∙8,314∙ ln(373/273)=3243,6 Дж/К.
-
при постоянном давлении
ΔS=(5/2)∙n∙R∙ ln(T2/T1)+R;
ΔS=(5/2)∙500∙8,314∙ln(373/273)+8,314=4539,4 Дж/К.
Ответ: 3243,6; 4539,4 Дж/К.
60. Рассчитайте изменение энтропии при нагревании 58,82 кг В2О3 от 298 до 700К, теплоемкость В2О3 Ср0=36,5525+106,345*10-3Т Дж/(моль*К).
Решение.
n(В2О3)=58820/70=840,3 (моль)
ST=∫T1T2(Ср(T)/T)dT=∫700298=(36,5525+106,345∙103/T/T)dT=840,3∙(36,5525ln(700/298)+106,345∙10-3∙840,3(700-298))=26230,2622+35923,40481=62153,7 Дж/К.
Ответ: 62153,7 Дж/К.
61. Бромбензол кипит при 429,8К, его теплота парообразования при этой температуре 241,9∙103 Дж/кг. Рассчитайте изменение энтропии при испарении 10 кг бромбензола.
Решение.
n(C6H5Br)=10/157=0,0637 моль,
S=0,0637∙241,9∙103∙ln(429,8/273)=6993,4 (Дж/К)
Ответ: 6993,4 (Дж/К)
62. Вычислите изменение энтропии при охлаждении 12∙10-3 кг (12 г) кислорода от 290 до 233К и одновременном повышении давления от 1,01∙105 до 60,6∙105 Па, если Ср=32,9 Дж/(моль∙К).
Решение.
n(О2)=12/32=0,375 моль;
S1=0,375∙32,9∙ln(233/290)=-2,7 Дж/(моль∙К)
S2=0,375∙32,9∙ln(60,6∙105 /1,01 ∙105)=50,51 Дж/(моль∙К)
S=50,51- 2,7=47,81 Дж/(моль∙К)
Ответ: 47,81 Дж/(моль∙К).
63.
Рассчитать изменение энтропии в процессе
нагревания 1 моля ртути от -77°С до 25 °С.
Теплота плавления ртути при t
= -38,9 °С равна 11,58 Дж г-1;
удельная теплоемкость твердой ртути
Ст
= 0,138 Дж
г-1;
удельная теплоемкость твердой ртути
Ст
= 0,138 Дж г-1
г-1 К-1,
жидкой ртути
К-1,
жидкой ртути
Сж
= 0,140 - 2,86 10
-6Т
Дж
10
-6Т
Дж г-1
г-1
 К-1
.Атомный вес ртути равен 200,6.
К-1
.Атомный вес ртути равен 200,6.
Решение.
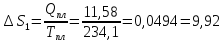 Дж
Дж моль-1
моль-1 К-1
К-1
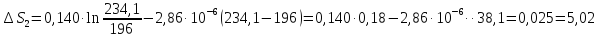 Дж
Дж моль-1
моль-1 К-1
К-1
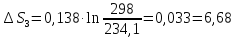 Дж
Дж моль-1
моль-1 К-1
К-1
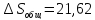 Дж
Дж моль-1
моль-1 К-1
К-1
Ответ:
 S
= 21,56 Дж
S
= 21,56 Дж моль-1
моль-1 К-1.
К-1.
64. Определить изменение энтропии, если 0,0112 м3 азота нагреваются от 0 до 50°С. Одновременно давление уменьшается от 1,013∙105 до 1,013∙103 н/м2. Теплоемкость равна 29,29 дж/моль∙град.
Решение.
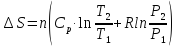
n=p 1V 1/RT 1=0,499 моль

Ответ: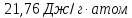
65. Как
изменится энтропия при нагревании 1
моль
хлорида натрия
от 25°С до 1073° К, если температура его
плавления 800°С, удельная теплота плавления
516,7 дж/г.
Мольная
теплоемкость
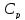 (т)
= 45,96+ 16,32∙
(т)
= 45,96+ 16,32∙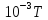 дж/моль∙град.
дж/моль∙град.
Решение.
Δ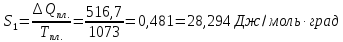
Δ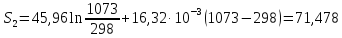

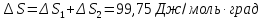
Ответ: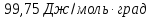
66. Найти изменение энтропии при нагревании 1 моль ацетона от 25 до 100°С, если удельная теплоту испарения ацетона равна 514,6 дж/г, температура кипения равна 56°С, мольные теплоемкости жидкого ацетона
СР(ж)=
125 дж/моль∙град,
паров ацетона
Ср(г) = 22,47 + 201,8∙ 63,5∙
63,5∙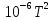 дж/моль∙град.
дж/моль∙град.
Решение.
Δ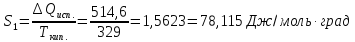
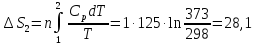

ΔS= Δ
Ответ: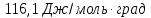
67. Рассчитать изменение энтропии при нагревании 2 моль метанола от 25 до 100°С, если удельная теплота испарения СН3ОН 1100,4 дж/г, температура кипения 64,7° С, мольные теплоемкости жидкого метанола СР(ж) = 81,56 дж/моль∙град и паров метанола
СР(г)=
15,28+ 105,2∙10 -3T—31,04∙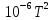 дж/моль∙град.
дж/моль∙град.
Решение.
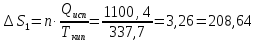
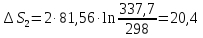
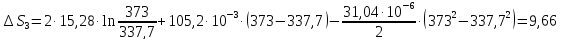
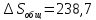 дж/моль∙град.
дж/моль∙град.
Ответ: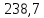 дж/моль∙град.
дж/моль∙град.
68. Определить
изменение энтропии при нагревании 1
моль
этанола от 25
до 100°С, если удельная теплота испарения
С2Н5ОН
863,6 дж/г,
температура
кипения 78,3°С, мольные теплоемкости
жидкого этанола
СР(ж)=
111,4 дж/моль∙град,
и паров этанола
Ср(г)= 19,07 +
212,7∙10-3T-108,6∙10-6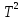 + 21,9∙
+ 21,9∙ дж/моль∙град.
дж/моль∙град.
Решение.
Δ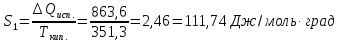
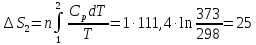
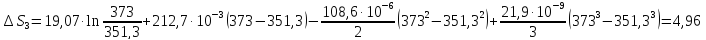
ΔS= Δ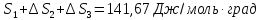
Ответ:
69. Найти
изменение энтропии при нагревании 1
моль
толуола от 25
до 150°С, если удельная теплота испарения
толуола 347,3 дж/г,
температура
кипения 110,6°С, мольные теплоемкости
жидкого толуола СР(ж)
= 166 дж/моль∙град
и паров толуола
СР
(г) = - 33,88
+557,0∙10-3T-342,4∙10-6 +79,87∙10-9
+79,87∙10-9 дж/моль∙град.
дж/моль∙град.
Решение.

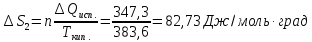
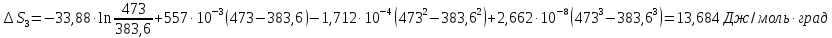

Ответ:
70. Как изменится энтропия при нагревании I моль моноклинной серы от 25 до 200°С, если удельная теплота плавления моноклинной серы 45,19 дж/г, температура плавления 119,3°С, мольные теплоемкости жидкой серы
СР
(ж) = 35,73 +1,17∙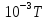 — 3,305 • 105
— 3,305 • 105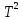 дж/моль∙град
и твердой серы
дж/моль∙град
и твердой серы
СР(т) = 23,64 дж/моль∙град.
Решение
Δ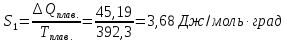
Δ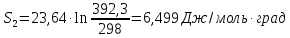
Δ
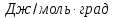
Δ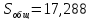
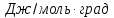
Ответ:
71. Определить изменение энтропии 1 моль хлорида натрия при нагревании от 20 до 850° С, если известно, что мольная теплоемкость твердого хлорида натрия составляет Ср(т) = 45,94+ 16,32∙10-3T дж/моль∙град и для жидкого соединения СР(ж) = 66,53 дж/моль∙град; теплота плавления 31,0 кдж/моль; температура плавления 800° С.
Решение


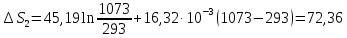
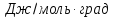
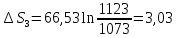


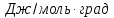
Ответ:

72.
Рассчитать прирост энтропии при смешении
250 см3
азота с 500 см3
кислорода при 1067 гПа и 27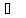 .
Чему равнялась бы работа при обратном
смешении газов?
.
Чему равнялась бы работа при обратном
смешении газов?
Решение.
ΔSсмеси=-R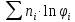
n(N2)=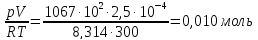
n(O2)=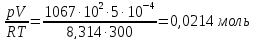
ϕ(N2)=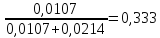
ϕ(O2)=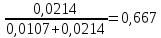
ΔSсмеси=-8,314∙(0,0107∙ln0,333+0,0214∙ln0,667)=0,17 Дж/моль
Ответ: 0,17 Дж/моль
73.
Вычислить изменение энтропии при
смешении 10 л водорода с 5 л метана, если
исходные газы и образующаяся смесь
газов находятся при 25 и 100 гПа.
и 100 гПа.
Решение.
р =100 гПа=100 102
Па
102
Па
25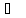 =298,15
К
=298,15
К
V(CH4)=5л=0,005 м3
V(H2)=10л=0,01 м3
n(H2)=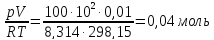
n(CH4)=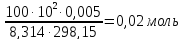
ϕ(H2)=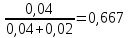
ϕ(CH4)=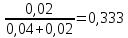
ΔSсмеси=-R
ΔSсмеси=-8,314∙(0,04∙ln0,667+0,02∙ln0,333)=-8,314∙(-0,038)=0,32 Дж/моль
Ответ: 0,32 Дж/моль
74. Вычислить изменение энтропии при разделения 1 моль воздуха при 1 атм. на чистые кислород и азот. Принять, что в воздухе 21% об. Кислорода и 79% об. азота.
Решение.
ΔS=n1Rln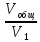 +n2Rln
+n2Rln
ΔS=0,21∙8,314ln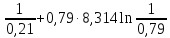 =(-2,72)+(-1,55)=-4,27
Дж/моль∙ К
=(-2,72)+(-1,55)=-4,27
Дж/моль∙ К
Ответ: -4,27 Дж/моль∙ К
75. Рассчитайте изменение энтропии при смешивании 1 моля водорода с 1 молем азота при н.у.
Решение.
V при н.у.=11,2 дм3
ΔS=
Ответ: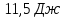
76.
В двух сообщающихся сосудах, разделенных
перегородкой, находится 1 моль азота и
2 моль кислорода. Перегородку вынимают,
газы смешиваются. Рассчитайте изменение
энтропии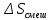 ,
если исходные температуры и давления
одинаковы, а объёмы различны;
,
если исходные температуры и давления
одинаковы, а объёмы различны;
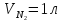 ;
;
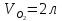 .Конечное
давление смеси равно исходному давлению
газа.
.Конечное
давление смеси равно исходному давлению
газа.
Решение.
Процесс смешения
газов необратим, и изменение энтропии
выражается неравенством
 .
Но если необратимый и обратимый процессы
проводятся в одних и тех же граничных
условиях, то
.
Но если необратимый и обратимый процессы
проводятся в одних и тех же граничных
условиях, то
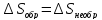 .
Всякий необратимый процесс можно
мысленно провести обратимо в несколько
стадий в тех же граничных условиях и
подсчитать энтропию для каждой обратимой
стадии. Тогда сумма изменений энтропии
этих стадий будет равна изменению
энтропии необратимого процесса. В данной
задаче общее изменение энтропии можно
заменить суммой изменения энтропий за
счёт расширения каждого из газов по
отдельности, т. е. принять, что
.
Всякий необратимый процесс можно
мысленно провести обратимо в несколько
стадий в тех же граничных условиях и
подсчитать энтропию для каждой обратимой
стадии. Тогда сумма изменений энтропии
этих стадий будет равна изменению
энтропии необратимого процесса. В данной
задаче общее изменение энтропии можно
заменить суммой изменения энтропий за
счёт расширения каждого из газов по
отдельности, т. е. принять, что
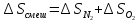 .
Согласно уравнению
.
Согласно уравнению
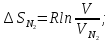
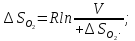
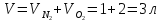
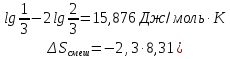
(
Ответ: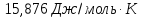
77.
Смешали 1 моль
аргона, взятого при
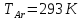 ,
с 2 моль азота, взятого при
,
с 2 моль азота, взятого при
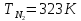 .
Исходные давления компонентов и конечное
давление смеси одинаковы. Вычислите
температурную составляющую энтропии
смешения. Теплоёмкость аргона
.
Исходные давления компонентов и конечное
давление смеси одинаковы. Вычислите
температурную составляющую энтропии
смешения. Теплоёмкость аргона
 =20,8
Дж/моль
=20,8
Дж/моль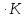 и азота
и азота
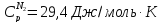
Решение.
Процесс смешения газов необратим, поэтому вычисляем общее приращение энтропии системы как сумму изменений энтропий компонентов за счёт увеличения температуры и за счёт уменьшения давления т.е.

Слагаемое является температурной составляющей
общего приращения энтропии в результате
смешения. Согласно уравнению
является температурной составляющей
общего приращения энтропии в результате
смешения. Согласно уравнению
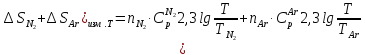 ,
,
T-конечная температура смеси, вычисляется по уравнению теплового баланса
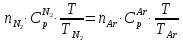 ,
,
Где
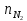 и
и
 -количества
молей аргона и азота. Подставляем числа
в уравнение:
-количества
молей аргона и азота. Подставляем числа
в уравнение:
29,4∙2(323-T)=20,8∙1(T-293)
После преобразования
уравнения и вычислений находим T=315
K.
Подставляем числа в уравнение
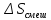

Ответ: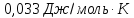
78. Рассчитайте изменение энтропии в процессе смешения 5 кг воды Т1=353К с 10 кг воды при Т2=290К. теплоемкость воды считать постоянной и равной 4,2 Дж/(моль∙К).
Решение.
n(Н2О)= 5000/18=278 моль;
n(Н2О)=10000/18=556 моль;
278∙4,4∙(Т- Т1)= 556∙4,2∙( Т2-Т);
3502,8Т=1089370,8;
Т=311К
S=556∙4,2∙ln(311/290) + 278∙4,4∙ln(311/353)=163,3-148= 15,3 Дж/(моль∙К).
Ответ: 15,3 Дж/(моль∙К).
79.
Определите
изменение энтропии при смешении 1 моль
аргона, взятого при TAr
= 293 К и
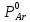 = 1,0133 • 105
Па с 2 моль азота, находящегося при
= 1,0133 • 105
Па с 2 моль азота, находящегося при
 =
1,0133
=
1,0133 105
Па и
105
Па и
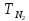 =
323 К. Давление смеси равно Рсм
= 1,0133∙105
Па. Принять аргон и азот идеальными
газами, а теплоемкость каждого газа
— величиной, постоянной в указанном
интервале температур и равной для азота
Сv
= 20,935 Дж/(моль∙К),
для аргона Сv=
12,561 Дж/(моль∙К).
=
323 К. Давление смеси равно Рсм
= 1,0133∙105
Па. Принять аргон и азот идеальными
газами, а теплоемкость каждого газа
— величиной, постоянной в указанном
интервале температур и равной для азота
Сv
= 20,935 Дж/(моль∙К),
для аргона Сv=
12,561 Дж/(моль∙К).
Решение.
nRT=pV
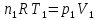
1∙8,314∙293=1,0133∙105∙V1
V1=0,02 м3

2∙8,314∙323=1,0133∙105∙V2
V2=0,05 м3
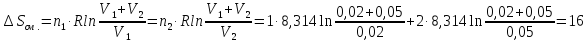 Дж/моль
Дж/моль
Ответ: 15,341 Дж/моль
80.
Определить
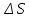 для
смешивания 1 моля азота с 3 молями
кислорода при
для
смешивания 1 моля азота с 3 молями
кислорода при
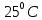 и общем конечном давлении 1 атм. Начальное
давление каждого газа 1 атм.
и общем конечном давлении 1 атм. Начальное
давление каждого газа 1 атм.
Решение.
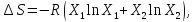
Где Х1 – мольная доля азота, а Х2 – мольная доля кислорода.
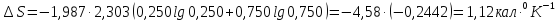
Ответ: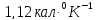
81.при давлении 2 атм занимают объем 30 л, до давления 1 атм и объема 100 л. Изобарная теплоемкость водорода Ср при этих условиях равна 29,3 Дж∙моль1∙К-1.
Решение.
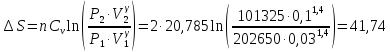
Ответ: ΔS = 41,74 Дж∙К-1
82. 2 моля N2 и 1 моль O2, находящиеся при 27 °С и 1 атм, смешиваются. После этого газовая смесь нагревается до 827 °С и сжимается до 5 атм. Найти изменение энтропии системы, если средние мольные теплоемкости (Сp) N2 и 02 равны, соответственно, 29,58 и 32,97 Дж∙моль-1∙К-1.
Решение.
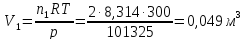

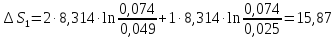 Дж ∙К-1
Дж ∙К-1
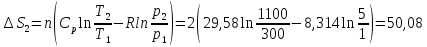 Дж ∙К-1
Дж ∙К-1
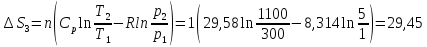 Дж ∙К-1
Дж ∙К-1
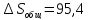 Дж ∙К-1
Дж ∙К-1
Ответ: ΔS = 95,40 Дж ∙К-1
83. Вычислить изменение энтропии при смешении 0,0001 м3 кислорода с 0,0004 м3 азота при постоянной температуре 17° С и давлении 1,013∙105 н/м2.
Решение.
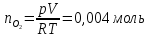

ΔS=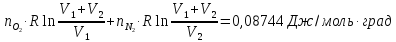
Ответ:
84. Смешаны 0,002 м3 гелия и 0,002 м3 аргона при 27°С и 1,013∙105 н/м2 каждый. После изотермного смешения полученная газовая смесь нагрета до 327°С при постоянном объеме. Вычислить общее возрастание энтропии, учитывая, что мольная теплоемкость обоих газов одинакова и равна
Cv(г)= 12,55 дж/моль∙град.
Решение.
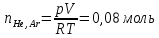
ΔS1=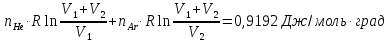
ΔS2=0,08 12,55∙ln
12,55∙ln
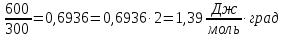
ΔS=2,3
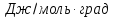
Ответ: 2,3
85. Вычислить изменение энтропии при разделении I моль воздуха при 1,013∙105 н/м2 на чистые кислород и азот (принять состав воздуха 21 об. % кислорода и 79 об. % азота).
Решение.
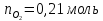
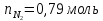
V(воздуха)=1л
V(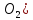 =0,21
л
=0,21
л
V(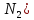 =0,79
л
=0,79
л
ΔS=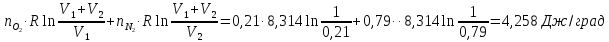
Ответ:
86. Рассчитать энтропию реакции 2H2(г)+CO(г)→CH3OH(г) при температурах 298,15 и 1000К, используя абсолютные энтропии соединений при Т=298,15 и р=1атм.:S0сн3OH=239,76 Дж/моль∙ К, S0H2=130,52 Дж/моль∙ К, S0СО=197,55 Дж/моль∙ К.
Зависимость теплоёмкости от температуры выражается уравнениями:
Ср(CH3OH)= Дж/моль
Дж/моль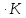
Ср(H2)=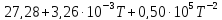 Дж/моль
Дж/моль
Ср(CO)= Дж/моль
Дж/моль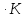
Решение.
ΔS298,15=239,76-2∙130,52-197,55=-218,83 Дж/ К
ΔS1000=-218,83+
Ответ: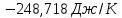 ;
-218,83 Дж/ К
;
-218,83 Дж/ К
87. Рассчитайте энтропию реакции CaCO3(кр)→CaO(кр)+CO2(г) при температурах 298,15 и 1200 К, используя абсолютные энтропии соединений при Т=298,15 и р=1атм.: S0CaO=38,07 Дж/моль∙К, S0CO2=213,66 Дж/моль∙К, S0CaCO3=91,71 Дж/моль∙К. Зависимость теплоёмкости соединений от температуры следующая:
Ср(CaO)=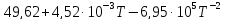 Дж/моль
Дж/моль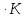
Ср(CO2)=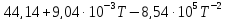 Дж/моль
Дж/моль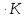
Ср(CaCO3)=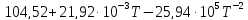 Дж/моль
Дж/моль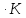
Решение.
ΔS298,15=213,66+38,07-91,71=160,02Дж/К
ΔS1200=ΔS298,15+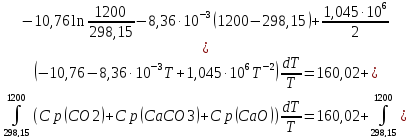
Ответ: 160,02Дж/К;

88.
Рассчитать энтропию реакции
2NaHCO3(кр)→Na2CO3(кр)+H2O(г)+CO2(г)
при температурах 298,15 и 500К на основании
абсолютных энтропий веществ при Т=298,15К
и р=1атм.:
S0Na2CO3=138,80
Дж/моль∙К, S0H2O=188,72
Дж/моль∙К, S0CO2=213,66
Дж/моль∙К, S0NaHCO3=102,10
Дж/моль∙К. Теплоёкость участников
реакции равна: Ср(Na2CO3)=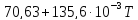 Дж/моль
Дж/моль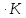
Ср(H2O)=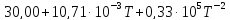 Дж/моль
Дж/моль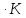
Ср(CO2)=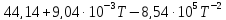 Дж/моль
Дж/моль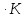
Ср(NaHCO3)= T
Дж/моль
T
Дж/моль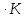
Решение.
ΔS298,15=213,66+188,72+138,8-2 102,10=336,98Дж/К
102,10=336,98Дж/К
ΔS500=336,98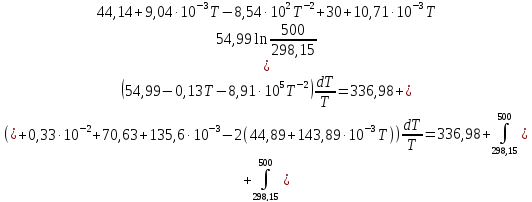
Ответ: 336,98Дж/К;
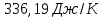
89.
Энтальпия плавления льда при 0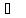 равна -6013 Дж/моль. Теплоёмкость Ср
льда и воды соответственно равна 37,24 и
75,30 Дж/моль∙ К. Найти изменение энтальпии
и энтропии для процесса:
равна -6013 Дж/моль. Теплоёмкость Ср
льда и воды соответственно равна 37,24 и
75,30 Дж/моль∙ К. Найти изменение энтальпии
и энтропии для процесса:
 H2O
(ж; -10
H2O
(ж; -10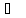 ;
1 атм.) H2O
(кр; -10
;
1 атм.) H2O
(кр; -10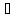 ;
1 атм.)
;
1 атм.)
Решение.
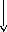
 -10
-10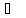 H2O(ж)
-10
H2O(ж)
-10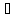 H2O(ж)
H2O(ж)
ΔS1=Cp∙ln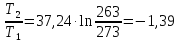 Дж/моль∙ К
Дж/моль∙ К
ΔS2=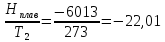 Дж/моль∙
К
Дж/моль∙
К
ΔS3=
Cp∙ln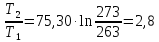 Дж/моль∙ К
Дж/моль∙ К
ΔSобщ= ΔS1+ ΔS2+ ΔS3=-1,39-22,01+2,8=-20,59 Дж/моль∙ К
ΔH=Cp(T2-T1)=37,24(0-10)=-372,4
ΔH2=-6013 ΔH3=75,30∙10=753
ΔH=-372-6013+753=-5632
Ответ: -20,59 Дж/моль∙ К; -5632
90. Вычислите изменение энтропии для реакции С2Н2+ 2Н2 = C2H6 в стандартных условиях при температуре 298 К.
Решение.
Энтропия - функция состояния системы, ее изменение определяется разностью значений абсолютных энтропии продуктов реакции и исходных веществ (с учетом
стехиометрических коэффициентов), и справочнике находим значения абсолютных энтропии участников реакции при температуре 298 К:
|
|
С2H2 |
H2 |
C2H6 |
|
|
48,00 |
31,21 |
54,85 |
 =
=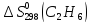 -
-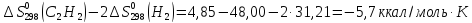
Ответ: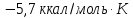
91.
Вычислите изменение энтропии
 S°
при стандартных условиях для реакций:
S°
при стандартных условиях для реакций:
2H2S+S02=2H2O(ж) + 3S;
Zn + H2S04 = ZnS04 + Н2;
СН4 + 202 = СО2 + 2Н20(пар)
Решение.
2H2S+S02=2H2O(ж) + 3S
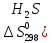 )=205,64
дж/моль∙град
)=205,64
дж/моль∙град
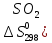 )=248,1
дж/моль∙град
)=248,1
дж/моль∙град
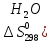 )=69,96
дж/моль∙град
)=69,96
дж/моль∙град
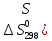 )=31,88
дж/моль∙град
)=31,88
дж/моль∙град
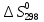 =
=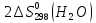 +
+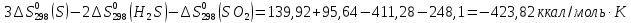
Zn + H2S04 = ZnS04 + Н2
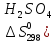 )=156,90
дж/моль∙град
)=156,90
дж/моль∙град
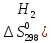 )=130,6
дж/моль∙град
)=130,6
дж/моль∙град
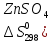 )=124,6
дж/моль∙град
)=124,6
дж/моль∙град
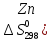 )=41,59
дж/моль∙град
)=41,59
дж/моль∙град
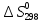 =
= +
+
СН4 + 202 = СО2 + 2Н20(пар)
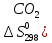 )=213,6
дж/моль∙град
)=213,6
дж/моль∙град
 )=205,03дж/моль∙град
)=205,03дж/моль∙град
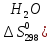 )=188,74
дж/моль∙град
)=188,74
дж/моль∙град
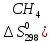 )=186,19
дж/моль∙град
)=186,19
дж/моль∙град
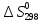 =
= +
+
Ответ: (-423,82; 56,71; -5,17 (Дж/К)
92.
Вычислите изменение энтропии
 S°
при стандартных условиях для реакций:
S°
при стандартных условиях для реакций:
2С2Н5С1 + 2Na = С4Н10 + 2NaCI,
2CH3OH = CH3-O-CH3 + Н20(ж),
С2Н5ОН + СНзСООН = Н3СООС2Н5 + Н20(ж).
Решение.
2С2Н5С1 + 2Na = С4Н10 + 2NaCI
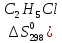 )=274,8
дж/моль∙град
)=274,8
дж/моль∙град
 )=51,42дж/моль∙град
)=51,42дж/моль∙град
 )=310
дж/моль∙град
)=310
дж/моль∙град
 )=72,36
дж/моль∙град
)=72,36
дж/моль∙град
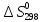 =
=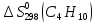 +
+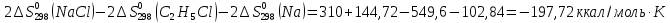
С2Н5ОН + СНзСООН = Н3СООС2Н5 + Н20(ж).
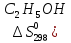 )=160,7
дж/моль∙град
)=160,7
дж/моль∙град
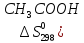 )=159,8
дж/моль∙град
)=159,8
дж/моль∙град
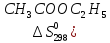 )=259
дж/моль∙град
)=259
дж/моль∙град
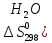 )=69,96
дж/моль∙град
)=69,96
дж/моль∙град
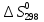 =
=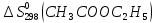 +
+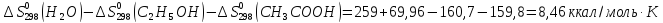
Ответ: (-197,72; 8,40 (Дж/К))
93.
Газообразные водород и хлор при 25
 поступают в реактор синтеза хлороводорода,
где взаимодействуют при 725
поступают в реактор синтеза хлороводорода,
где взаимодействуют при 725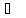 по реакции:
по реакции:
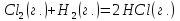 .
Определите изменение энтропии системы,
начиная с момента поступления газов в
реактор, если их объёмный расход одинаков.
.
Определите изменение энтропии системы,
начиная с момента поступления газов в
реактор, если их объёмный расход одинаков.
Решение.
Процесс состоит из
трёх стадий: смешения исходных веществ,
нагревания их до 725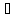 и химического превращения. В соответствии
с этим, изменение энтропии системы
включает энтропии: смешения (
и химического превращения. В соответствии
с этим, изменение энтропии системы
включает энтропии: смешения (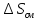 );
изобарического нагревания компонентов
(
);
изобарического нагревания компонентов
( )
и реакции (
)
и реакции (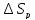 ).
).
Исходная смесь
состоит из 1 моль
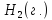 и 1 моль
и 1 моль
 ,
следовательно, молярные доли компонентов
перед началом реакции одинаковы и равны:
,
следовательно, молярные доли компонентов
перед началом реакции одинаковы и равны:
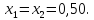 Отсюда имеем:
Отсюда имеем:
 Дж/К
Дж/К
Определяем изменение энтропии при изобарном нагревании компонентов системы по отдельности:
Для
 -
-
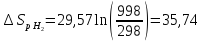 Дж/К
Дж/К
Для
 -
-
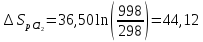 Дж/К
Дж/К
где 29,57 и 36,50 - значения изобарных теплоёмкостей водорода и хлора.
Изменение энтропии системы на стадии химического превращения определяем по закону Гесса.
Для водорода -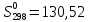 Дж/моль
∙К
Дж/моль
∙К
Для хлора -
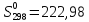 Дж/моль ∙К
Дж/моль ∙К
Для хлороводорода
-
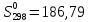 Дж/моль ∙К
Дж/моль ∙К
Отсюда, воспользовавшись следствием закона Гесса, имеем:
 Дж/К
Дж/К
Cуммируя результаты расчётов для всех трёх стадий процесса, имеем:
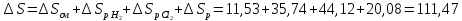 Дж/К
Дж/К
Ответ:
 Дж/К
Дж/К

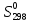 ,ккал/моль
,ккал/моль