
Решение_задач_исследования_операций
.pdf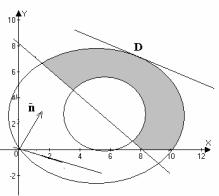
81
прямым - есть вектор n = (1; 3) . Перемещаем линию уровня в
направлении нормали до тех пор, пока она не станет касательной к верхней окружности.
Рис. 2.12
Обозначим точку касания буквой D; в этой точке значение Z будет максимальным. Угловой коэффициент касательной K равен угловому
коэффициенту прямой x + 3x |
|
= z |
|
. Значит, k = − |
1 |
. |
1 |
2 |
|
0 |
3 |
||
|
|
|
|
|||
С другой стороны, угловой коэффициент касательной для
окружности ( x − 5)2 |
+ (x − 3)2 |
= 36, |
|
найдем, дифференцируя это уравнение |
|||||||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
по переменной x : |
2 (x − 5) + 2 (x − 3) x |
′ = 0 |
|
||||||||
|
|
1 |
|
1 |
|
2 |
|
|
2 |
|
|
Отсюда, |
x ′ = − |
x1 − 5 |
|
. |
|
|
|
|
|
|
|
|
2 |
x2 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решим систему уравнений: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x − 5 |
|
1 |
|
|
|
|
|
|
|
− |
1 |
|
= − |
|
, |
|
|
|
|
|
|
x − 3 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
( x − 5)2 |
+ ( x |
− 3)2 = 36; |
|||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
x |
= 3x −12, |
|
|
||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
( x − 5)2 |
+ (3x −15)2 |
= 36; |
|||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
x |
= 3x −12, |
|
|
||||
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x 2 − 50x + 107 = 0. |
|
||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Одно решение |
этой |
системы |
x |
= |
|
25 − 3 |
10 |
|
; x = |
15 − 9 10 |
является |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
2 |
5 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
посторонним, |
потому, |
что |
x2 |
не |
удовлетворяет |
условию |
|||||||||||||||||||
неотрицательности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Другое решение: |
x |
= |
25 + 3 10 |
≈ 6, 9; x |
= |
|
15 + 9 |
10 |
≈ 8, 7 дает координаты |
||||||||||||||||
|
|
|
1 |
|
|
|
5 |
|
|
|
|
2 |
5 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
точки D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
70 + 30 10 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При этом Z |
max |
= x + 3x |
= |
= 14 + 6 10 . |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
2 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения минимального значения функции цели будем перемещать линию уровня в направлении, противоположном вектору нормали n , до тех пор, пока у нее не окажется одна общая точка с областью допустимых решений. Такой точкой является точка Е = (8; 0) .
Значит, Zmin |
= 8 , если x1 = 8; x2 = 0 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
при x = |
25 + 3 |
10 |
; x = |
15 + 9 10 |
|
|||
Ответ: Z |
max |
= 14 + 6 10 |
; |
|||||||||
|
|
|
||||||||||
|
|
|
1 |
5 |
2 |
5 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Zmin = 8 , если x1 = 8; x2 = 0 .
Пример 2.6. Для задачи с дробно-линейной целевой функцией и линейной системой ограничений графическим методом найти глобальные экстремумы (максимум и минимум), если математическая модель задачи имеет вид:
z = 2x1 − x2 (max, min ), x1 + x2
2x1 − 3x2 ≥ −13,
x1 + x2 ≥ 6,
4x1 − x2 ≤ 19, x1 ≥ 0, x2 ≥ 0.
Решение. Найдем область определения допустимых значений для переменных x1; x2 определим на плоскости X1 0 X 2 множество решений системы ограничений (рис. 2.13)

83
Рис. 2.13
Областью допустимых значений (множеством решения системы неравенств) является множество точек, расположенных внутри треугольника ABC. Выразим x2 через значение функции z и переменную x1, из выражения для целевой функции
z= 2x1 − x2 , x1 + x2
z( x1 + x2 ) = 2x1 − x2 ,
zx1 + zx2 = 2x1 − x2 ,
x2 (z + 1) = (2 − z ) x1,
x = |
2 |
− z |
x |
2 |
z |
+ 1 |
1 |
|
|
Данному соотношению удовлетворяют точки, принадлежащие
прямой x |
= k x |
с угловым коэффициентом k = |
2 − z |
. |
|
||||
2 |
1 |
z + 1 |
||
|
|
|
||
Значит, линиями уровня функции цели являются прямые, проходящие
через начало координат с угловым коэффициентом k = 2 − z . z + 1
Определим предельные значения угловых коэффициентов для семейства прямых, являющихся линиями уровня и имеющими общие точки с множеством допустимых значений. Пусть угол α1 равен углу между осью OX1 и радиус-вектором OA, а угол α2 равен углу между осью OX2 и радиус-вектором OB, тогда должно выполняться условия tg α1 ≤ k ≤ tg α2 .
Найдем координаты точки А; для этого решим систему уравнений
84
x1 + x2 = 6,
4x1 − x2 = 19.
Получим x1 = 5; x2 = 1. значит, tg α1 = 1 .
5
Найдем координаты токи В; для этого решим систему уравнений
2x1 − 3x2 = −13,
x1 + x2 = 6.
Получим, x1 = 1; x2 = 5. Значит, tg α2 = 5 .
Таким образом, имеем неравенства |
1 |
≤ k ≤ 5 , |
1 |
≤ |
2 − z |
≤ 5 . |
|||||||
|
|
|
|
|
|
5 |
|
|
|
5 z + 1 |
|||
Решим систему неравенств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
≤ |
2 − z |
, |
|
6z − 9 |
≤ 0, |
||||||
|
5 |
|
z + 1 |
|
z + 1 |
|
|
|
|
|
|||
|
2 |
− z |
|
|
|
6z + 3 |
|
|
|
|
|
||
|
≤ 5; |
|
≥ 0. |
||||||||||
|
|
|
|
|
z + 1 |
||||||||
z + 1 |
|
|
|
|
|
|
|
|
|||||
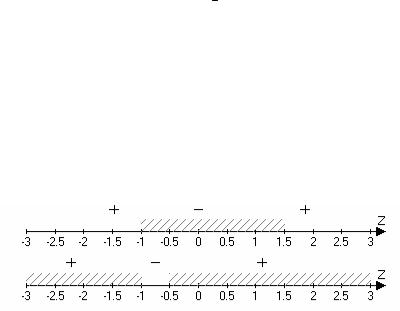
Каждое из этих неравенств решаем методом интервалов
Общее решение системы неравенств: −0, 5 ≤ z ≤ 1, 5
Таким образом, zmin = −0, 5 ; это значение достигается в точке А(5; 1). zmax = 1, 5 ; это значение достигается в точке В(1; 5)
Ответ:
zmin = −0, 5 |
при |
x1 = 5; x2 = 1; |
zmax = 1, 5 |
при |
x1 = 1; x2 = 5. |
Пример 2.7. Графическим методом найти максимум и минимум целевой функции, если математическая модель задачи имеет вид:
z = (x + 1)2 + ( x + 2)2 |
(max, min) |
||||
|
|
1 |
|
2 |
|
2x + 3x |
|
≥ 6 |
|
||
|
1 |
|
2 |
≤ 18 |
|
3x1 − 2x2 |
|
||||
|
|
+ 2x2 |
≤ 8 |
|
|
− x1 |
|
||||
x1 ≥ 0; x2 ≥ 0
Решение. Найдем и изобразим на плоскости X1OX2 множество решений системы ограничений (рис. 2.14). Область допустимых решений состоит из внутренних точек многоугольника ABCDE. Линии

85
уровня представляют собой окружности с центром в точке О1(-1; -2). Глобальный максимум находится в точке В, как самой удаленной от точки О1. Глобальный минимум находится в точке F, в которой окружность касается прямой проходящей через ED. Точка В является точкой пересечения прямых (II) и (III), для определения координат этой точки решим систему уравнений:
3x1 − 2x2 = 18,
− x1 + 2x2 = 8.
Рис. 2.14
Получим значения x1 = 13; x2 = 10,5. При этом zmax = 142 + 12, 52 = 352, 25 .
Для определения координат точки F в начале получим уравнение прямой, проходящей через точки E(0; 2) и D(3; 0)
x1 |
− 0 |
= |
x2 |
− 2 |
. |
|
3 − 0 |
0 − 2 |
|||||
|
|
|||||
Отсюда, получим уравнение прямой ED x2 = − 2 x1 + 2 .
3
Угловой коэффициент этой прямой k1 = − 2 .
3
Найдем теперь уравнение прямой, проходящей через точку О1(-1; 2) перпендикулярно к прямой ED. Угловой коэффициент этой прямой K2 определим из условия перпендикулярности прямых: k1 k2 = −1 . Значит,
k2 |
= |
3 |
. Уравнение прямой O1F запишем в виде: |
x2 |
+ 2 = |
3 |
( x1 + 1) . |
|
|
||||||
|
2 |
|
|
2 |
|
||
Отсюда, получим уравнение прямой O1F: x2 = 3 x1 − 1 .
2 2
Для определения координат точки F решим систему:

86
Получим, x1 |
= |
15 |
; x2 = |
16 |
. |
||||||
|
|
|
|
||||||||
|
|
13 |
|
|
|
13 |
|
||||
|
|
15 |
2 |
|
16 |
||||||
Тогда, zmin |
= |
|
|
|
+ 1 |
+ |
|
||||
|
|
||||||||||
|
|
13 |
|
|
13 |
||||||
|
|
x |
|
= − |
2 |
x + 2, |
|||||
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
3 1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
x |
|
= |
x − |
. |
|||||
|
|
|
|
|
|||||||
|
|
|
|
2 |
2 |
|
1 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|||
+ 2 |
2 |
= |
2548 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
169 |
|
|
|
|
|
||
Ответ:
z |
|
= |
2548 |
|
при |
x |
= |
15 |
; x = |
16 |
; |
|
|
min |
169 |
|
|
1 |
13 |
2 |
13 |
|
|||
|
|
|
|
|
|
|
||||||
zmax |
= 352, 25 |
при |
x1 = 13; x2 = 10, 5. |
|||||||||
Пример 2.8. Найти |
условный |
экстремум |
|
функции Z = x + 2 y при |
||||||||
условии x2 + y2 = 5 методом Лагранжа.
Решение. Методом множителей Лагранжа используется для решения задач нелинейного программирования.
Пусть задана задача линейного программирования
L = f(M) = (x1;x2;…xn ) → max (min)
при ограничениях: gi(x1, x2,…xn ) = 0, i=1,1m .
Пусть функции f(x1, x2,…xn ) и g(x1, x2,…xn ) непрерывны вместе со своими частными производными. Так как ограничения заданы в виде уравнений, то для решения задачи воспользуемся методом отыскивания условного экстремума функции нескольких переменных, который сводится к исследованию на обычный экстремум функции
Лагранжа. |
|
|
|
|
L(x1, x2,…xn,λ1,…, ,λm) = f(x1, x2,…xn)+ ∑m λ |
|
g |
(x , x |
2 ,…xn ) , |
k =1 |
k |
|
k 1 |
|
где λk (k= 1m ) – множители Лагранжа.
Необходимое условие наличия условного экстремума выражаются системой (n+m) уравнений:
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L(M ) |
= 0,(i =1m), |
||||||
|
|
∂x |
||||||
|
|
|
i |
|||||
g |
|
(M ) = 0,(k = |
|
), |
||||
k |
1m |
|||||||
|
|
|
|
|
|
|
|
|
из которых могут быть найдены неизвестные где M0 (x10 , x20 ,..., xn0 ) -
точка, в которой возможен условный экстремум.
Достаточные условия наличия условного экстремума связана с изучением знака 2-го дифференциала функции Лагранжа:
d 2 L( x10 , x20 ,..., xn0 , λ10 ,..., λ0m , dx1 ,..., dxn )
87
для каждого набора значений x20 ,..., xn0 , λ10 ,..., λ0m , полученный из системы (1) при условии, что dx1,…,dxn удовлетворит уравнениям:
n ∂g |
k |
(M |
0 |
) |
|
|
|
|
||
∑ |
|
|
|
|
dxj = 0, k = 1, m |
|||||
|
|
|
|
|
|
|||||
g =1 |
∂xj |
|
|
|
|
|
|
|
||
dx 2 |
+ dx |
2 |
+ ... + dx |
2 |
≠ 0 . |
|||||
1 |
|
|
2 |
|
|
n |
|
|
||
Функция L=f(M) имеет условный максимум в точке M0, если для всевозможных значений dx1,…,dxn, удовлетворяющих условиям (2), выполняется неравенство:
d2 L(x10 , x20 ,..., xn0 , λ10 ,..., λ0m , dx1 ,..., dxn ) < 0
иусловный минимум, если при этих условиях:
d2 L( x10 , x20 ,..., xn0 , λ10 ,..., λ0m , dx1 ,..., dxn ) > 0 .
Вслучае двух переменных при одном ограничении g(x;y)=0, то функция Лагранжа имеет вид:
L(x;y;λ)=f(x;y)+ λg(x;y).
Система для нахождения стационарных (критических) точек состоит из трёх уравнений:
|
∂L |
= 0 , |
∂L |
= 0 , g(x;y)=0. |
|
|
|
||
|
∂x |
∂y |
||
Если M ( x0 , y0 ), λ0 - любой |
из решений этой системы, вместо |
|||
изучения знака второго дифференциала, можно исследовать знак определителя .
|
0, |
|
|
g ′ |
(M |
0 |
) |
|
g ′ |
(M |
) |
|
|
||
|
|
|
|
x |
|
|
|
|
y |
|
0 |
|
|
. |
|
= − |
g ′ |
(M ) L′′ |
(M ) L′′ |
(M ) |
|||||||||||
|
x |
|
0 |
|
xx |
|
|
|
0 |
|
xy |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
g ′ |
|
(M ) L′′ |
(M ) L′′ |
(M ) |
|
|||||||||
|
y |
0 |
|
xy |
|
|
|
0 |
|
yy |
|
|
0 |
|
|
При этом:
1)если <0, то функция Z = f(x;y) имеет в точке M0 условный максимум,
2)если >0, то функция Z = f(x;y) имеет в точке M0 условный минимум.
Для нашей задачи составляем функцию Лагранжа:
L(x;y; λ)=x+2y+ λ(x2+y2=5).
Находим частные производные: ∂∂Lx =1+ λ x; ∂∂Ly = 2 + 2λ y.
Система уравнений принимает вид:

88
|
|
|
|
|
|
|
1+ 2λ x = 0, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
+ λ y = 0, |
|
|
|||||
|
|
|
|
|
|
|
x2 + y2 = 5. |
|
|
||||||
Решаем систему: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = − |
1 |
, |
|
|
|
|
|||||||
|
|
2λ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = − 1 |
, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
+ |
|
1 |
= 5, |
|
λ |
2 = 1 |
|
||
|
|
|
|
|
|
|
, |
||||||||
|
|
|
4λ |
|
|
|
λ |
|
|
|
|
4 |
|
||
|
λ = |
1 |
|
, |
|
|
|
|
|
|
λ = − 1 |
, |
M1 (-1,-2); |
||
|
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|||||
x = −1, |
|
|
|
|
|
|
x2 |
= 1, |
|
M2 (1,2). |
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
= 2, |
|
||
y = −2, |
|
|
|
|
|
|
y2 |
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее находим вторые частные производные функции Лагранжа и составляем второй дифференциал d2L:
′′ |
′′ |
= 0 |
′′ |
= 0 |
′′ |
= 2λ . |
Lxx |
= 2λ ; Lxy |
; L yx |
; L yy |
Следовательно d2L=2λ(dx2+dy2)
При λ2=1/2 d2L>0, следовательно в точке M1(-1;-2) функция имеет условный минимум, равный: Zmin (M1 ) = −5 .
При λ2= -1/2 d2L>0, следовательно, в точке M2(1;2) функция имеет максимум, равный: Zmax (M2 ) = 5
Теперь определить тип экстремумов в стационарных точках другим
способом (с помощью определителя |
|
): |
|
|
|
|
|||||||
|
|
|
|
g(x; y) = x 2 + y2 − 5 g′ |
= 2x; |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
′ |
|
′′ |
= 2λ ; |
′′ |
= |
0 |
′′ |
|
′′ |
= 2λ . |
|
|
|
= 2 y; |
Lxx |
Lxy |
; L yx = 0 |
; L yy |
|||||||
|
|
g y |
|
|
|
|
|
|
|
|
|
|
|
При λ = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
−2 |
−4 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
1 = |
−2 |
1 |
0 |
= 20 > 0 |
|
|
||
|
|
|
|
|
|
−4 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следовательно, в точке M1(-1;-2) для λ=1/2 функция Z=x+2y имеет условный минимум, равный Zmin(M1)=-5;
При λ = − |
1 |
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
2 |
4 |
|
|
|
0 |
|
||||
|
|
2 = |
2 −1 |
0 |
= −20 < 0 |
|
|
4 |
0 |
1 |
|
||

89
следовательно, в точке M2(1;2) для λ=-1/2 функция имеет условный максимум, равный Zmax(M2)=5.
Ответ: Zmin = (M1 ) = −5, Zmax = (M 2 ) = 5.
Пример 2.9. Применяя метод Лагранжа, найти точки условного экстремума функции U = xy + yz при заданных ограничениях:
x2 + y2 = 2,
y + z = 2.
x, y, z -целочисленные координаты. Решение. Составляем функцию Лагранжа:
L=xy+yz+λ1(x2+y2-2)+ λ2(y+z-2).
Находим частные производные функции Лагранжа:
L′ = y + 2λ x ; L′ |
= x + z + 2λ y + λ |
; L′ = y + λ ; L′ = x2 + y2 − 2; L′ = y + z − 2. |
||||||
x |
1 |
y |
1 |
2 |
z |
2 |
λ1 |
λ2 |
Для нахождения стационарных точек, получаем систему уравнений:
y + 2λ1 x = 0,
x + z + 2λ1 y + λ2 = 0,
y + λ2 = 0,x2 + y2 = 2,y + z = 2;
|
|
|
|
|
|
|
|
|
|
|
= −λ2 |
|
|
(из3) |
|||
y |
|
|
||||||
|
|
= |
|
λ2 |
|
|
|
|
x |
|
|
|
|
|
(из1, 3) |
||
2λ1 |
|
|
||||||
|
|
|
|
|
|
|||
|
|
= 2 − y = 2 + λ2 |
|
|||||
z |
(из5 и1) |
|||||||
|
λ |
|
|
|
|
|
|
|
|
|
2 |
|
+ 2 + λ2 − 2λ1λ2 + λ2 = 0 |
(из2) |
|||
|
|
|||||||
2λ1 |
|
|
|
|
|
|
||
λ22 |
|
+ λ |
2 |
= 2 |
(из4) |
|||
|
4λ 2 |
|
2 |
|||||
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
Можно показать, что из последних уравнений системы следует уравнение четвертой степени относительно λ1 :
16λ14 − 32λ13 + 8λ1 −1 = 0
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|||||
Корни этого уравнения: |
λ1(1) |
= − |
; λ1( 2) = |
; λ1(3) = 2 − 3; λ1( 4) = 2 + 3. |
||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
||
а) при значении λ (1) = − |
1 |
, получим λ = −1; x = 1; y = 1; z = 1. |
Стационарная |
|||||||||||||
|
||||||||||||||||
|
1 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точка M1 (1;1;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
при значении λ (2) |
= |
1 |
|
, |
получим λ |
|
= −1; x = −1; y = 1; z = 1. Стационарная |
||||||||
|
|
|
||||||||||||||
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
точка M1 (−1;1;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
значения λ1 = 2 ± |
|
|
|
|
являются |
|
посторонними |
корнями, им |
|||||||
|
3 |
|
|
|
||||||||||||
соответствуют стационарные точки с не целочисленными координатами (не соответствуют условию задачи).
Далее, находим вторые частные производные функции L и составляем второй дифференциал d 2 L :
90
|
L′′ = 2λ ; L′′ |
= 1; |
L′′ = 0; |
L′′ = 1; |
L′′ |
= 2λ ; L′′ = 1; |
L′′ = 0; |
L′′ = 1; |
L′′ = 0. |
|
||||
|
xx |
1 |
|
xy |
|
xz |
yx |
yy |
1 |
yz |
zx |
zy |
zz |
|
Следовательно d 2 L = 2λ dx2 |
+ 2dxdy + 2λ dy2 + 2dydz . |
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
Из условий связи следуют равенства: |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
xdx + ydy = 0, |
|
|
|
|
|
||
|
|
|
|
|
|
|
dy + dz = 0. |
|
|
|
|
|
||
Исследуем |
знак |
d 2 L |
для |
первой |
стационарной |
точки |
при |
|||||||
λ1 = −0, 5; λ2 |
= −1; M1 (1;1;1) : |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
dx + dy = 0, |
|
|
|
|
|
||
|
|
|
|
|
|
|
dy + dz = 0. |
|
|
|
|
|
||
Откуда получаем: |
|
|
|
|
|
|
|
|
|
|||||
|
|
dx = −dy; dz = −dy d 2 L (M |
) = −dy2 |
− 2dy2 − dy2 − 2dy2 < 0 |
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Значит, |
в точке M1 (1;1;1) |
функция имеет условный максимум, равный |
||||||||||||
Lmax (M1 ) = 1 1 + 1 1 = 2 . |
|
|
|
|
|
|
|
|
|
|||||
Исследуем |
знак |
d 2 L |
для |
второй |
стационарной |
точки |
при |
|||||||
′ |
′ |
|
2 |
( |
|
) |
|
|
|
|
|
|
|
|
λ1 |
= 0, 5; λ2 = −1; M |
|
−1;1;1 : |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
−dx + dy = 0, dx = dy, |
|
|
|
|
||||
|
|
|
|
|
|
dy + dz = 0; |
dz = −dy. |
|
|
|
|
|||
поэтому d 2 L (M |
2 |
) = dy2 + 2dy2 |
+ dy2 − 2dy2 = 2dy2 |
> 0 . |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит, в точке M 2 (−1;1;1) функция имеет условный минимум, равный
Lmin (M 2 ) = −1 1 + 1 1 = 0 .
Ответ: Lmax (M1 ) = 1 1 + 1 1 = 2 ,
Lmin (M 2 ) = −1 1 + 1 1 = 0 .
Контрольные вопросы к индивидуальным заданиям № 2
1.Как записывается общий вид математической модели транспортной задачи?
2.Какие виды транспортных задач Вы знаете?
3.Что представляет целевая функция в транспортной задаче?
4.Какое основное отличие закрытой и открытой транспортных задач?
5.Что называется опорным решением транспортной задачи?
6.Какие существуют методы получения первого опорного плана?
7.В чем суть этих методов?
8.Что называется циклом пересчета в транспортной задаче?
9.Каковы основные правила сдвига по циклу?
10.В чем состоит суть методов потенциала?
