Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский государственный технологический университет им. В.Г. Шухова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Решение_задач_исследования_операций

.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

707.24 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Имеем, Zmin	= −2	при x1 = 4; x2		= 0; x3 = 0; x4 = 2 .
Ответ:	Zmax	= 8	при x1 = 0; x2 = 2; x3 = 2; x4 = 0 ,
Zmin = −2			при x1 = 4;	x2	= 0; x3 = 0; x4 = 2 .
Пример 1.2. Решить задачу линейного программирования
			Z = 3x1 + 2x2 → max (min ) ;
			−x1 + 2x2 ≤ 4,
			2x1 − x2 ≤10,
			x + x ≥ 2,
			1		2
				x1 ≥ 0, x2 ≥ 0.
графическим методом.
Решение.	Изобразим			на	плоскости	множество	точек,
удовлетворяющих			первому	неравенству		системы ограничений:
− x1 + 2x2 ≤ 4 .
Границей этого множества является прямая						− x1 + 2x2 = 4 ,	которая

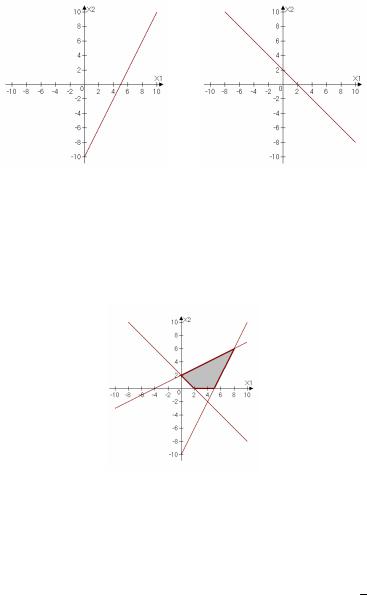
проходит через две точки (0; 2) и (-4; 0). Эта прямая делит плоскость на две части; координаты точки (0; 0) удовлетворяют неравенству − x1 + 2x2 ≤ 4 , поэтому, множеством решений неравенства будет та

полуплоскость, которая содержит точку (0; 0) – полуплоскость под прямой (рис. 1.4).

Рис. 1.4

Аналогично, строим полуплоскости для второго и третьего неравенств системы ограничений задачи (рис.1.5, 1.6).

Рис. 1.5	Рис.1.6
Учитывая условия неотрицательности	переменных x1 ≥ 0, x2 ≥ 0 ,

получим, что область допустимых решений состоит из точек, принадлежащих выделенному четырехугольнику(рис 1.7).

Изобразим линию уровня функции цели для z = 0 3x1 + 2x2 = 0 .

Рис. 1.7


Эта прямая	проходит через точки (0; 0) ,					(−2; 3) .	Находим
направление роста функции цели. Оно задаётся вектором								= (3; 2) .
							n
Координаты вектора			есть коэффициенты при			переменных x1, x2
		n
функции цели.	Вектор				перпендикулярен линиям уровня функции
				n

цели. Направление убывания функции цели задаётся вектором −n . В нашем случае −n = (−3; − 2) . Перемещаем линию уровня вдоль

направления n , пока у неё не окажется только одна общая точка с областью допустимых решений. Аналогично поступаем для

определения

минимума

функции цели,

перемещая линию уровня

z = 0 в направлении, противоположном

. C – точка максимума

функции цели, B – точка минимума функции цели:

− x + 2x

= 4

2 ,

= 18,

= 6,

C(I,II)

C(8; 6)

2x − x = 10 ↓ +, x1

= 2x2 − 4,

x1 =

2 6 − 4 = 8,

B (I, III)

− x + 2x = 4,

3x = 6,

x = 2,

B(0; 2)

+ x2 = 2,

x1 = 2 − x2 , x1 =

Zmax (C) = 3 8 + 2 6 = 36 ,

Zmin (B) = 3 0 + 2 2 = 4 .

Ответ: Zmax

= Z (C) = 36 при C(8; 6) ,

Zmin = Z (B) = 4 при B(0; 2) .

Пример 1.3. Симплексным методом решить задачу линейного программирования при оптимизации функции цели на максимум.

Z = x1 + 2x2 → max ,

−2x1 + x2 ≤ 2,
	− 2x ≤ 2,
x	− 2x ≤ 2,
1	2
x1	+ x2 ≤ 5,

x1 ≥ 0, x2 ≥ 0.

Решение. Задача задана в стандартной форме, поэтому для применения симплекс-метода запишем её в канонической форме. Для этого водим добавочные, новые неотрицательные переменные x3, x4, x5 (если знак неравенства ≤, то добавочная переменная прибавляется, если знак неравенства ≥, то добавочная переменная отнимается).

Функцию цели также переписываем в виде: f (z; x1 ,..., xn ) = 0 .

Получаем:

Z − x1 − 2x2 = 0,

−2x1 + x2 + x3 = 2,

x1 − 2x2 + x4 = 2,x1 + x2 + x5 = 5.

Заполняем первую симплексную табл. 1.13. Таблица включает столбцы: шаг – номер таблицы по порядку, БП – базисные переменные на i-м шаге, z, xi (i = 1, 2, …) – переменные, заданные в задаче, плюс добавочные переменные, b – свободные члены, Σ - сумма всех

элементов строки, λ - оценочные отношения, равные bi xi

(рассматриваются только неотрицательные отношения), действия над строками.

Таблица 1.13

Шаг	БП	z	x1		↓x2	x3	x4	x5	b	Σ	λ					Действия
		1	-	-2		0	0	0	0	-	-					2(I	н)	+
		1	1	-2		0	0	0	0	2	-					(0)→(0)
			1							2						(0)→(0)
			-									2		= 2min		(I) →(I н)
	x3		-		1	1	0	0	2	2		2
	x3		2		1	1	0	0	2	2	1
			2

0												2			= −1 → ∞	2(I	н)	+
	x4		1	-2		0	1	0	2	2		2				(II)	→(II
	x4		1	-2		0	1	0	2	2						(II)	→(II
												− 2				н)
	x5		1	1		0	0	1	5	8		5	= 5			(I н) + (III)
	x5		1	1		0	0	1	5	8	1		= 5			→(III н)
																→(III н)

На 0-шаге: x3, x4, x5. - базисные переменные (чаще всего добавочные переменные), x1, x2. - свободные переменные.

Решение 0-шага: x1 = 0, x2 = 0, x3 = 2, x4 = 2, x5 = 5.

Так как все переменные базисного решения неотрицательны, то оно называется допустимым опорным планом.

Применяем симплекс-метод:

1)так как в (0)-строке имеются отрицательные оценки, то найденное решение не является оптимальным;

2)выбираем ведущий столбец – столбец с наименьшей отрицательной оценкой в (0)-строке;

2)выбираем ведущую строку – строка с наименьшим оценочным

отношением λ (рассматриваются только неотрицательные оценки):

	1		2		5	= min {2; ∞; 5} = 2 ,
min		;		;
min		;		;
	2		−2		1

Следовательно, ведущей будет (I)-строка. Переменная x3 выводится из базиса, x2 становится базисной;

4)находим ведущий элемент – на пересечении ведущих строки столбца;

5)применяем гауссово преобразование так, чтобы в ведущем столбце стояли 0, кроме одного ведущего элемента, который равен 1;

6)повторяем шаги 1)-5).

На 2 шаге в (0)-строке нет отрицательных оценок, следовательно, оптимальное решение найдено: x1 = 1, x2 = 4, x3 = 0, x4 = 9, x5 = 0, (табл. 1.14)

Базисные переменные: x1, x2, x4. Свободные переменные: x3, x5.

Причём: Z = 9 − 1 x3 − 5 x5 → max .

3 3

Таблица 1.14

																				25

Ша		Б	z		x1		x2		x3		x4	x5	b	Σ				λ		Действия
г		П	z		x1		x2		x3		x4	x5	b	Σ				λ		Действия
г		П
			1	-5			0		2		0	0	4	2						5(IIIн)+
			1	-5			0		2		0	0	4	2						(0)→(0н)
																				(0)→(0н)
																2		= −1 → ∞		2(IIIн)+(I)
		x2		-2			1		1		0	0	2	2		− 2		= −1 → ∞		2(IIIн)+(I)
		x2		-2			1		1		0	0	2	2						→(Iн)
																				→(Iн)

1															6			= −2	→ ∞	3(IIIн)+(II)
		x4		-3			0		2		1	0	6	6		− 3		= −2	→ ∞	3(IIIн)+(II)
		x4		-3			0		2		1	0	6	6						→(IIн)
																				→(IIн)

																3	= 12min			(Iн)	1
		x5			3		0		-1		0	1	3	6		3				(Iн)
		x5			3		0		-1		0	1	3	6	3					3
																				3
																				→(IIIн)
																				→(IIIн)
									1			5		1
			1	0			0				0		9
									3			3
														2
														2

									1			2
		x2		0			1				0		4	6
		x2		0			1		3		0	3	4	6
2									3			3
2

		x4		0			0		1		1	1	9	1
		x4		0			0		1		1	1	9	2
														2
									−	1		1
		x1		1			0		−		0		1	2
		x1		1			0		3		0	3	1	2

Zmax	= 9 .
Ответ: Zmax				= 9		xопт		= (1; 4; 0; 9; 0) .

Замечание: при решении ЗЛП на минимум возможны два пути:

1) отыскать максимум функции F, полагая F = −Z и учитывая, что

Zmin = −Fmax ;

2) модифицировать симплекс-метод, на каждом шаге уменьшая линейную функцию цели за счёт той переменной, которая в (0)-строке содержит наибольшую положительную оценку.

Пример 1.4. Решить ЗЛП методом искусственного базиса

Z = 3x1 + 2 x2 → max,

	− x + 2 x			≤ 4,
	1		2
2 x1 − x2			≤ 10,
	− x1 − 2 x2 ≤ −2,

x1 ≥ 0, x2		≥ 0.

x1, x2 , x5 . Исходный опорный план:

x3 , x4 , y1 ;

Решение. Приведём ЗЛП к каноническому виду, для этого вводим дополнительные неотрицательные переменные x3 , x4 , x5 :

Z = 3x1 + 2x2 → max,

− x1 + 2x2 + x3 = 4,

2x1 − x2 + x4 = 10,

− x1 − 2x2 + x5 = −2.

Первое базисное решение: x1 = 0, x2 = 0, x3 = 4, x4 = 10, x5 = −2 .

Так как среди базисных переменных есть одна, принимающая отрицательное значение, то базисное решение не является допустимым и симплекс-метод применять нельзя. Для каждой отрицательной переменной вводим искусственную неотрицательную переменную, одновременно изменяя функцию цели.

Получаем новую задачу, для которой известен исходный опорный план, это так называемая M-задача.

Z = 3x1 + 2x2 − M y1 → max,

где M − достаточно большое положительное число

− x + 2x2 + 3x3 = 4,

2x1 − x2 + x4 = 10,

x1 + 2x2 − x5 + y1 = 2.

В опорном решении М–задачи базисными являются те базисные переменные, которые были положительными в исходной задаче, плюс вновь введенные искусственные переменные. Остальные переменные

– свободные, включая те базисные переменные, которые были отрицательными. В нашем случае: базисные переменные

свободные переменные

x1 = 0, x2 = 0, x3 = 4, x4 = 10, x5 = 0, y1 = 2, z = 0

Данное базисное решение является допустимым и можно применять симплекс-метод. Новая М-задача решается обычным симплексметодом, только первая симплекс-таблица дополняется еще одной М- строкой. Если на каком-то шаге искусственная переменная y1

становится свободной, то столбец y1 из дальнейшего рассмотрения исключается. Выразим функцию цели через свободные переменные:

y1 = 2 − x1 − 2x2 + x5 ,

Z= 3x1 + 2x2 − M (2 − x1 − 2x2 + x5 ) = (3 + M ) x1 + (2 + 2M )x2 − Mx5 − 2M ,

Z− (3 + M )x1 − (2 + 2M )x2 + Mx5 − 2M = 0.

Заполним симплекс-табл. 1.15 и решаем задачу. По симплексной таблице анализируем полученные результаты.

																											Таблица 1.15

Шаг	БП	z			x1	x2	x3	x4	x5		y1	b	∑	λ												Действия

		1	-3			-2	0	0	0		0	0	-4									2(III H ) + (0) → (0 H )

			-M			-	0	0	M		0	-	-									2M (III H ) + (M 0 )
			-M			2M	0	0	M		0	2M	4M									→ (M 0 H )
																						→ (M 0 H )
0	x3		-1			2	1	0	0		0	4	6		4	= 2						−1 (III H ) + (I )
0	x3		-1			2	1	0	0		0	4	6	2		= 2						→ (I H )
														2								→ (I H )

	x4		2			-1	0	1	0		0	10	12		12		= −6 → ∞					(III				) + (II ) → (II					)
	x4		2			-1	0	1	0		0	10	12				= −6 → ∞					(III			H	) + (II ) → (II				H	)
															−2										H					H
															−2
														2						min		(III )				1	→ (III
	y1		1			2	0	0	-1		1	2	5			= 1←												H	)
	y1		1			2	0	0	-1		1	2	5	2		= 1←										2		H	)
														2												2

		1	-2			0	0	0	-1		1	2	0									2 (IIIн) + (0) → (0н)

		0	0			0	0	0	0		M	0	M

	x3		-2			0	1	0	1			2	2		2		= −1 → ∞					2 (IIIн) + (I ) → (Iн)
	x3		-2			0	1	0	1			2	2		−2		= −1 → ∞					2 (IIIн) + (I ) → (Iн)
															−2
1				5						1							2			22			−5	(IIIн) + (II )
	x4					0	0	1	−			11	14	11					=			2		(IIIн) + (II )

			2							2										5
			2							2							5			5		→ (IIн)
																						→ (IIн)


				1					−	1						2					min	(III ) 2 → (IIIн)
	x2					1	0	0				1	2	1				= 2		←
	x2			2		1	0	0		2		1	2	1		1		= 2		←
				2						2						1

																				28
																				Окончание табл. 1.15

Ш	БП	z	x1		x2			x3			x	x5	y1	b	∑	λ								Действия
аг	БП	z	x1		x2			x3			4	x5	y1	b	∑	λ								Действия
		1	0	4				0			0	-3		6	8		6		= −6 → ∞		3 (IIн) + (0) → (0н)
		1	0	4				0			0	-3		6	8				= −6 → ∞		3 (IIн) + (0) → (0н)
																	−1
	x3		0	4				1			0	-1		6	10						(IIн) + (I ) → (Iн)

2																	6	= 3				1
2	x4		0	-5					0		1	2		6	4	2		= 3						(II ) → (IIн)

																			min		2
																			min		2
																←
	x1		1	2				0			0	-1		2	4		2		= −2 → ∞		(IIн) + (III ) → (IIIн)
	x1		1	2				0			0	-1		2	4				= −2 → ∞		(IIн) + (III ) → (IIIн)
																	−1

				−		7				3												7
		1	0				0					0		15	14								(Iн) + (0) → (0н)
										2
																					2
						2
						2


					3					1												2		(I ) → (Iн)
	x3		0				1					0		9	12
					2					2
3					2					2											3
																					3


				−		5				1												5		(Iн) + (II ) → (IIн)
	x5		0	−		2	0			2		1		3	2							5
	x5		0				0					1		3	2						2



				−		1				1											1
	y1		1	−			0			2		0		5	6						1		(Iн) + (III ) → (IIIн)
	y1		1			2	0			2		0		5	6							2	(Iн) + (III ) → (IIIн)

							7		8
		1	0	0								0		36	42
		1	0	0			3		3			0		36	42
							3		3

							2		1
	x3		0	1								0		6	8
	x3		0	1			3		3			0		6	8
							3		3
4
4							5			4
							5			4
	x5		0	0								1		18	22
	x5		0	0			3		3			1		18	22
							3		3

							1			2
	x1		1	0								0		8	10
	x1		1	0			3			3		0		8	10
							3			3

Так как в (0)-строке все оценки положительны, то, соответственно, критерий оптимальности решения ЗЛП на максимум выполнен и оптимальное решение задачи найдено: 1) базисные переменные x1=10; x2=8; x5=22; 2) свободные переменные x3=0; x4=0; 3) оптимальное значение Zmax = 36 .

Функция цели через свободные переменные выражается равенством:

Z = 36 − 7 x3 − 8 x4 → max . 3 3

Ответ: zmax = 36, , x*=(10; 8; 0; 0; 22).

Пример 1.5. Решить ЗЛП, заданную в канонической форме, методом искусственного базиса.

Z = 3x1 + 2x2 + x3 − 8x4 → max,

3x1 + 3x2 + 4x3 − 7 x4 = 10,2x1 + x2 + x3 − 2x4 = 2,

xi ≥ 0, i = 1, 4.

Решение. Вводим искусственные (неотрицательные) переменные y1 и y2 и формулируем новую задачу:

Z = 3x1 + 2x2 + x3 − 8x4 − M ( y1 + y2 ) → max,

3x1 + 3x2 + 4x3 − 7x4 + y1 = 10,

2x1 + x2 + x3 − 2x4 + y2 = 2, xi ≥ 0, i = 1, 4, y j ≥ 0, j = 1, 2.

Находим исходный опорный план: 1) базисные переменные: y1 = 10 ; y2 = 2 ; 2) свободные переменные: x1 = 0, x2 = 0, x3 = 0, x4 = 0 .

Так как значения переменных неотрицательны, то данное решение допустимое и можно применить симплекс-метод.

Чтобы применить симплекс-метод нужно функцию цели выразить через свободные переменные:

y1 = 10 − 3x1 − 3x2 − 4x3 + 7 x4 , y2 = 2 − 2x1 − x2 − x3 + 2x4 ,

y1 + y2 = 12 − 5x1 − 4x2 − 5x3 + 9x4

Z= 3x1 + 2x2 + x3 − 8x4 − M (12 − 5x1 − 4x2 − 5x3 + 9x4 ) =

=(3 + 5M )x1 − (2 + 4M )x2 − (1 + 5M )x3 + (8 + 9M )x4 − 12M ,

Z− (3 + 5M ) x1 − (2 + 4M )x2 − (1 + 5M )x3 + (8 + 9M )x4 −12M = 0.

Заполняем симплекс-табл. 1.16 и находим решение ЗЛП.

																							30
																					Таблица 1.16

Шаг		z	x1	x2	x3	x4	x5	y1	b	∑								λ			Действия

			-3	-2	-1	8	0	0	0	3									(1 + 5M )(IIн) + (0) → (0н)
		1																	(1 + 5M )(IIн) + (0) → (0н)
		1	-	-	-	9M	0	0	-	-
			5М	4M	5M	9M	0	0	12M	17M
0		y1	3	3	4	-7	1	0	10	14		10		=			5		−4 ( IIH ) + ( I ) → ( IH )
		y1	3	3	4	-7	1	0	10	14				=					−4 ( IIH ) + ( I ) → ( IH )
											4					2
											2							min	( II ) → ( IIH )
		y2	2	1	1	-2	0	1	2	5					= 2 ←
		y2	2	1	1	-2	0	1	2	5	1				= 2 ←
											1
			-1	-1	0	6	0	1	2	8									(0) − (6 − М )(Iн) → (0н)
		1
		1	5M	M	0	-M	0	5M	-2M	8M
			5M	M	0	-M	0	5M	-2M	8M
1
1		y1	-5	-1	0	1	1	-4	2	-6		2			= −1 → ∞				( I ) → ( IH )
												2

												−2
		x3	2	1	1	-2	0	1	2	5	1		2			= 2 ←			( II ) + 2 ( IH ) → ( IIH )
													2					min
													1

		1	29	5	0	0			-10	18

			0	0	0	0			0	M
			0	0	0	0			0	M
2		x4	-5	-1	0	1			2	-2									( IIH ) + ( I ) → ( IH )

		x	-8	-1	1	0			6	0										1	(II ) → (II		)
		3																	2			H
																			2
	Так как искусственные переменные																y1 , y2 стали свободными, то

столбцы y1 , y2 из дальнейшего рассмотрения можно исключить.

Так как в (0)–строке все элементы положительны, то задача решена,

имы нашли оптимальное решение:

1)базисные переменные: x3=6, x4=2;

2)свободные переменные: x1=0, x2=0, y1=0, y2=0.

Оптимальное значение Zmax	= −10; выражение функции цели через
свободные переменные: Z = −10	− 29x1 − 5x2 → max.

Ответ: Zmax = −10, x*=(0; 0; 6; 2).

Пример 1.6. Для исходной задачи, заданной в стандартной форме, составить математическую модель двойственной задачи.

По решению двойственной или исходной задачи найти решение другой с использованием основных теорем двойственности.

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.12.2018118.78 Кб11реферат по информатике.doc
#
11.03.201547.7 Кб13Реферат социология.docx
#
01.09.201989.6 Кб14реферат.doc
#
11.03.20157.12 Mб171Реферат.docx
#
06.05.201933.76 Кб62решение 2 задание.docx
#
18.04.2015707.24 Кб34Решение_задач_исследования_операций.pdf
#
11.03.20151.29 Mб143решенные задачи госэкзамен.docx
#
11.03.20154.81 Mб32Роботы.pdf
#
11.03.201526.2 Кб14Романская архитектура германии.docx
#
25.09.201931.3 Кб3Руденко , информатика.docx
#
27.08.2019269.82 Кб2РУП Правовая информатик 2011 специалитет 030501...doc