Решение_задач_исследования_операций

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белгородский государственный технологический университет им. В.Г. Шухова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Таблица 1.11

.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

707.24 Кб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

							11
							Таблица 1.8

Вариант			Задача	Вариант			Задача
	z = 4x1 − 2x2 → max,				z = x1 − x2 → max,
1	2x1 + 3x2 ≤ 18,			2	−2x1 + 3x2 ≤ 9,
1				2

	− x1 + 3x2 ≤ 9,				x1 − 2x2 ≤ 2,

	2x1 − x2 ≤ 10,				x1 + x2 ≤ 8,
	xi ≥ 0; i = 1, 2.				xi	≥ 0; i = 1, 2.
						Продолжение табл. 1.8

Вариант			Задача	Вариант			Задача
	z = 3x1 − 4x2 → max,				z = x1 − 3x2 → max,
3	x1 + 2x2 ≤ 4,			4	−2x1 + 3x2 ≤ 6,
3				4

	x1 + x2 ≤ 3,				x1 + 3x2 ≤ 15,
			≤ 8,
	2x1 + x2		≤ 8,		3x1 − x2 ≤ 15,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = 5x1 + 4x2 → max,				z = 3x1 + 2x2 → max,
5	− x + 2x		≤ 12,	6	2x − x		≤ 8,
5		1	2	6		1	2
	5x1 − 4x2 ≤ 20,				− x1 + 2x2 ≤ 8,

	x1 ≤ 8,				x1 ≤ 6,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = 3x1 + 5x2 → max,				z = 3x1 + 5x2 → max,
7	x1 ≤ 8,			8	−2x1 + x2 ≤ 2,
7				8

	− x1 + 2x2 ≤ 12,				2x1 − x2 ≤ 10,

	−3x1 + 2x2 ≤ 8,				− x1 + 2x2 ≤ 10,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = x1 + 2x2 → max,				z = 2x1 + 4x2 → max,
9	− x1 + 2x2 ≤ 7,			10	x1 − x2 ≤ 5,
9				10

	x1 + x2 ≤ 11,				−3x1 + 2x2 ≤ 8,

	x1 ≤ 8,				x2 ≤ 7,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

11	z = 4x1 + 3x2 → max,				z = 3x1 + 5x2 → max,
11	−3x1 + 4x2 ≤ 32,				x1 + x2 ≤ 9,
	−3x1 + 4x2 ≤ 32,			12	x1 + x2 ≤ 9,
			≤ 19,	12

	2x1 + x2				3x1 − 2x2 ≤ 12,

	3x1 − x2 ≤ 21,				x1 + 4x2 ≤ 16,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = 6x1 + 3x2 → max,					z = 3x1 + 4x2 → max,
13	− x + 2x			≤ 18,	14	x + 2x		≤ 20,
13		1	2		14	1	2
	5x1 + x2 ≤ 53,					− x1 + 2x2 ≤ 8,
			≤ 4,
	x1 − 2x2		≤ 4,			3x1 − x2 ≤ 18,
	xi	≥ 0; i = 1, 2.				xi ≥ 0; i = 1, 2.

						Продолжение табл. 1.8

Вариант			Задача	Вариант			Задача
	z = 5x1 + 4x2 → max,				z = 2x1 − 4x2 → max,
15	− x1 + x2 ≤ 1,			16	3x1 + 2x2 ≤ 18,


	x1 − 2x2 ≤ 1,				− x1 + 2x2 ≤ 10,
							≤ 9,
	2x1 + x2 ≤ 22,				3x1 − x2
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.
	z = −4x1 + 3x2 → max,				z = 3x1 + 4x2 → max,
17	2x1 + x2 ≤ 4,			18	4x1 − 3x2 ≤ 32,
							≤ 21,

	x1 + 2x2 ≤ 8,				x1 − 3x2
							≤ 19,
	x1 + x2 ≤ 3,				x1 + 2x2
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = − x1 + x2 → max,				z = 3x1 + 6x2 → max,
19	3x1 − 2x2 ≤ 9,			20	−2x1 + x2 ≤ 4,
							≤ 18,

	x1 + x2 ≤ 8,				2x1 − x2
							≤ 53,
	−2x1 + x2 ≤ 2,				x1 + 5x2
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = −3x1 + x2 → max,				z = 4x1 + 5x2 → max,
21	3x + x		≤ 15,	22	2x − x		≤ 12,
		1	2			1 2
	3x1 − 2x2 ≤ 6,				x2 ≤ 8,

	− x1 + 3x2 ≤ 15,				−4x1 + 5x2 ≤ 20,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.
	z = 4x1 + 5x2 → max,				z = 2x1 + 3x2 → max,
23	−4x1 + 5x2 ≤ 20,			24	2x1 − x2		≤ 8,


	2x1 − x2 ≤ 12,				x2 ≤ 6,

	x2 ≤ 8,				− x1 + 2x2 ≤ 8,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

	z = 5x1 + 3x2 → max,					z = 5x1 + 3x2 → max,
25	2x − x			≤ 12,	26	2x − x		≤ 10,
25		1	2		26		1 2
	2x1 − 3x2 ≤ 8,					x1 − 2x2		≤ 2,

	x2 ≤ 8,					− x1 + 2x2 ≤ 10,
	xi	≥ 0; i = 1, 2.				xi	≥ 0; i = 1, 2.

Окончание табл. 1.8

Вариант			Задача	Вариант			Задача
	z = 2x1 + x2 → max,				z = 4x1 + 2x2 → max,
27	x1 + x2 ≤ 11,			28	− x1 + x2		≤ 5,


	x2 ≤ 8,				x1 ≤ 7,

	2x1 − x2 ≤ 7,				2x1 − 3x2 ≤ 8,
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.
	z = 5x1 + 3x2 → max,				z = 4x1 + 3x2 → max,
29	x + x		≤ 9,	30	2x + x		≤ 20,
		1	2			1 2
	4x1 − x2 ≤ 16,				− x1 + 3x2 ≤ 18,
							≤ 8,
	−2x1 + 3x2 ≤ 12,				2x1 − x2
	xi	≥ 0; i = 1, 2.			xi	≥ 0; i = 1, 2.

Задание 4

Методом искусственного базиса найти решение задачи линейного программирования при оптимизации функции цели на максимум или минимум. Варианты заданий приведены в табл. 1.9.

Таблица 1.9

Вариант		Задача	Вариант			Задача
	z = x1 + x2 → max,			z = 4x1 + 3x2 → max,
1	x1 + 2x2	≤ 10,	2	− x1 + 2x2 ≤ 8,
1		≥ 2,	2		+ x2	≥ 4,

	x1 + 2x2			2x1
		≤ 10,			− x2	≤ 8,
	2x1 + x2	≤ 10,		2x1	− x2	≤ 8,
	xi ≥ 0, i = 1, 2.			xi ≥ 0, i = 1, 2.

	z = −x1 + 2x2 → max,			z = 5x1 + 4x2 → max,
3	4x1 − 2x2 ≤ 12,		4	2x1 + x2		≥ 8,
		+ 3x2 ≤ 6,				≤ 16,

	− x1			2x1 − x2
		+ 4x2 ≥ 16,
	2x1			− x1 + 3x2 ≤ 12,
	xi ≥ 0, i = 1, 2.			xi ≥ 0, i = 1, 2.

	z = 2x1 + 2x2 → max,			z = 3x1 − x2 → max,
5	3x1 − 2x2 ≥ −6,		6	4x1 + x2 ≥ 4,
		+ x2 ≥ 3,			+ x2 ≤ 6,

	3x1			x1
					≤ 2,
	x1 ≤ 3,			x1
	xi ≥ 0, i = 1, 2.			xi ≥ 0, i = 1, 2.

					Продолжение табл. 1.9

Вариант			Задача	Вариант		Задача
	z = 4x1 + 3x2 → max,				z = 3x1 + x2 → max,
7	3x1 − x2 ≥ 3,			8	x1 + x2 ≥ 2,
		− 2x2	≤ 2,

	x1				x1 − x2 ≥ 1,
		+ 2x2	≤ 10,
	x1				x1 ≤ 4,
	xi ≥ 0, i = 1, 2.				xi	≥ 0, i = 1, 2.

	z = 3x1 + x2 → max,				z = 2x1 + 3x2 → max,
9	3x1 + 2x2 ≥ 6,			10	x1 + x2 ≥ 4,
			≤ 9,

	3x1 − x2				−2x1 + 3x2 ≤ 18,
		≤ 6,
	x2				5x1 − x2 ≤ 20,
	xi ≥ 0, i = 1, 2.				xi	≥ 0, i = 1, 2.
	z = 4x1 + 2x2 → max,				z = 2x1 − x2 → max,
11	−2x1 + 3x2 ≤ 6,			12	3x1 − x2 ≤ 6,
			≤ 12,

	3x1 − x2				4x1 + 2x2 ≥ 16,
		+ 4x2	≥ 8,
	x1				−2x1 + 4x2 ≤ 12,
	xi ≥ 0, i = 1, 2.				xi	≥ 0, i = 1, 2.
	z = 2x1 + x2 → max,				z = 2x1 + 2x2 → max,
13	x1 + x2 ≥ 1,			14	x2 ≤ 3,
			≤ 6,

	3x1 − x2				x1 + 3x2 ≥ 3,

	− x1 + 3x2 ≤ 6,				−2x1 + 3x2 ≥ −6,
	xi ≥ 0, i = 1, 2.				xi	≥ 0, i = 1, 2.

	z = 2x1 + 5x2 → max,			z = 3x1 + 4x2 → max,
15	x1 + 2x2 ≥ 4,		16	− x1 + 3x2 ≥ 3,
15		+ 3x2 ≤ 12,	16

	− x1			2x1 + x2 ≤ 10,

	x1 + x2 ≤ 8,			−2x1 + x2 ≤ 2,
	xi ≥ 0, i = 1, 2.			xi ≥ 0, i = 1, 2.

	z = 3x1 + 6x2 → max,			z = x1 + 3x2 → max,
17	x1 + x2 ≥ 2,		18	2x1 + 3x2 ≥ 6,
17		− x2 ≤ 8,	18

	2x1			x1 ≤ 6,
		+ 2x2 ≤ 8,
	− x1	+ 2x2 ≤ 8,		− x1 + 3x2 ≤ 9,
	xi ≥ 0, i = 1, 2.			xi ≥ 0, i = 1, 2.

Окончание табл. 1.9

Вариант			Задача	Вариант			Задача
	z = 6x1 + 3x2 → max,				z = 3x1 + 4x2 → max,
19	x1 + 2x2		≤ 16,	20	2x1 − x2		≤ 8,
						+ 2x2 ≤ 8,

	− x1 + 4x2 ≥ 8,				− x1
			≥ 6,				≥ 4,
	3x1 − x2				x1 + 2x2
	xi ≥ 0, i = 1, 2.				xi ≥ 0, i = 1, 2.

	z = x1 + x2 → max,				z = 4x1 + 5x2 → max,
21	x1 + 2x2		≤ 10,	22	3x1 − x2		≤ 12,
			≤ 10,			+ 2x2 ≤ 16,

	2x1 + x2				− x1
			≥ 2,				≥ 8,
	2x1 + x2				x1 + 2x2
	xi ≥ 0, i = 1, 2.				xi ≥ 0, i = 1, 2.

	z = −x1 + 3x2 → max,				z = x1 + 2x2 → max,
23	x2 ≤ 2,			24	3x1 − x2 ≤ 6,
		+ 4x2	≥ 4,			+ 3x2 ≤ 6,

	x1				− x1
		+ x2 ≤ 6,
	x1				x1 + x2 ≥ 1,
	xi ≥ 0, i = 1, 2.				xi ≥ 0, i = 1, 2.

	z = x1 + 3x2 → max,				z = 5x1 + 2x2 → max,
25	− x1 + x2 ≥ 1,			26	x1 + x2 ≤ 8,
		+ x2 ≥ 2,				+ x2	≥ 4,

	x1				2x1
		≤ 4,				− x2	≤ 12,
	x2				3x1
	xi ≥ 0, i = 1, 2.				xi ≥ 0, i = 1, 2.

	z = 3x1 + 2x2 → max,				z = 6x1 + 3x2 → max,
27	− x1 + 5x2 ≤ 20,			28	2x1 − x2 ≤ 8,
							+ 2x2 ≤ 8,

	x1 + x2 ≥ 4,				− x1

	3x1 − 2x2 ≤ 18,				x1 + x2 ≥ 2,
	xi	≥ 0, i = 1, 2.			xi	≥ 0, i = 1, 2.
	z = 2x1 + 4x2 → max,				z = 3x1 + 6x2 → max,
	3x − 2x		≤ 6,		2x + x ≤ 16,
29		1	2	30		1	2
	4x1 + x2 ≥ 8,				4x1		− x2 ≥ 8,

							+ 3x2 ≥ 6,
	− x1 + 3x2 ≤ 12,				− x1
	xi	≥ 0, i = 1, 2.			xi	≥ 0, i = 1, 2.

Задание 5

Для исходной задачи, заданной в стандартной форме, составить математическую модель двойственной задачи. По решению двойственной (или исходной) задачи найти решение другой задачи с использованием основных теорем двойственности. Решение исходной задачи (или двойственной) найдите графическим методом и симплексным методом. Варианты задания 5 приведены в таблице для вариантов задания 4.

Задание 6

Для исходной задачи, записанной в канонической форме, составить математическую модель двойственной задачи, решить её графическим методом. По решению двойственной задачи найти решение исходной задачи с использованием основных теорем двойственности. Найти также решение двойственной задачи по известному решению исходной задачи (полученному в задании 2) с использованием основных теорем двойственности. Варианты задания 6 приведены в таблице для вариантов задания 2.

Рекомендации по решению индивидуальных заданий № 1

Пример 1.1. Преобразовать задачу из канонической формы к стандартной. Графическим методом найти значения неизвестных, при которых целевая функция принимает наибольшее и наименьшее значения.

Z = − x1 + 5x2 − x3 + x4 (max, min),

3x1 + 5x2 + 2x3 + x4 = 14,4x1 + 10x2 + x3 + 3x4 = 22,

xi ≥ 0 , i = 1, 2, 3, 4.

Решение. Запишем соотношение, определяющее функцию цели Z, в виде уравнения и добавим его к системе ограничений

z + x1 − 5x2 + x3 − x4 = 0,
	+ 5x2 + 2x3	+ x4 = 14,
3x1
	+ 10x2 + x3	+ 3x4 = 22.
4x1

Заполним симплексную табл. 1.10

						Таблица 1.10

z	x1	x2	x3	x4	b
						нулевая строка
1	1	-5	1	-1	0	нулевая строка
						первая строка
0	3	5	2	1	14	первая строка
						вторая строка
0	4	10	1	3	22	вторая строка

Будем выполнять линейные преобразования Жордана-Гаусса такие, чтобы в преобразованной таблице были единичные столбцы, например, в столбце x4 будет один элемент, равный единице, а остальные элементы равны нулю, для этого выполним над строками преобразования

(0) + (I ) → (0)

(II ) − 3(I ) → (II )

Врезультате получим табл. 1.11

На втором шаге выполним преобразования, чтобы столбец для x2 стал единичным:

(I ) + (II ) → (I )

−1 (II ) → (II )

Врезультате получим табл. 1.12.

Таблица 1.12

z	x1	x2	x3	x4	b

1	4	0	3	0	14

0	-2	0	-3	1	-6

0	1	1	1	0	4

Переменные x2 и x4 называются базисными, а переменные x1, x3 – свободными. Последней таблице соответствуют задачи

Z = −4x1 − 3x3 + 14 (max, min),

−2x1 − 3x3 + x4 = −6,

x1 + x2 + x3 = 4,

xi ≥ 0, i = 1, 2, 3, 4.

Отсюда получим

Z = −4x1 − 3x3 + 14 (max, min),

x4 = −6 + 2x1 + 3x3 ,

x2 = 4 − x1 − x3 ,

xi ≥ 0, i = 1, 2, 3, 4.

Поскольку переменные x4, x2 могут по условию принимать только неотрицательные значения, то уравнение-равенство можно записать в виде неравенств:

Z = −4x1 − 3x3 + 14 (max, min),

−6 + 2x1 + 3x3 ≥ 0,

4 − x1 − x3 ≥ 0,

xi ≥ 0; x3 ≥ 0.

В результате получим задачу линейного программирования в стандартной форме, в которой остались две переменные

Z = −4x1 − 3x3 + 14 (max, min),

2x1 + 3x3 ≥ 6,

x1 + x3 ≤ 4, x1 ≥ 0; x3 ≥ 0.

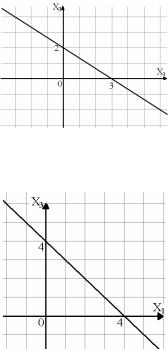
Решим задачу графическим методом. В прямоугольной декартовой системе координат строим прямую 2x1 + 3x3 = 6, соответствующую первому ограничению и выделяем полуплоскость над прямой, точки которой являются решением неравенства 2x1 + 3x3 ≥ 6 (рис.1.1).

Рис. 1.1

Построим теперь прямую x1 + x3 = 4, соответствующую второму ограничению и выделим полуплоскость под прямой, точки которой удовлетворяют неравенству x1 + x3 ≤ 4 (рис.1.2).

Рис. 1.2

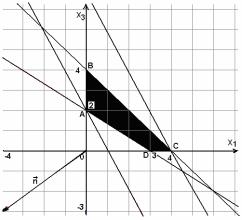
Находим теперь общую часть полуплоскостей решений, учитывая условия неотрицательности переменных x1, x3 (находим область допустимых значений, рис. 1.3).

Рис 1.3

Строим нормаль линий уровня n = (−4, −3) . При нахождении максимума целевой функции линию уровня (прямую, перпендикулярную нормали) перемещаем в направлении нормали до тех пор, пока не найдём последнюю общую точку с областью допустимых решений x1 = 0; x3 = 2.

При нахождении минимума целевой функции линию уровня перемещаем в направлении, противоположном нормали, до крайней точки x1 = 4; x3 = 0.

Можно также, вместо перемещений линий уровня, найти координаты всех угловых точек области допустимых решений A(0;2), B(0:4), C(4:0), D(3:0), вычислить значения функции z в этих точках и выбрать наибольшее и наименьшее значения. В нашем случае z(A)=8; z(B)=2; z(C)=-2; z(D)=2.

Имеем:

Zmax	= 8	при	x1	= 0;	x3 = 2,
Zmin	= −2	при	x1	= 4;	x3 = 0 .

Подставим координаты точки A в выражения для x2 и x4. Найдём их значения для максимума z:

x4 = −6 + 2 0 + 3 2 = 0, x2 = 4 − 0 − 2 = 2.

Значит Zmax = 8 при x1 = 0; x2 = 2; x3 = 2; x4 = 0 .

Аналогично найдём значения переменных x2 и x4 при минимуме z x4 − 6 + 2 4 + 3 0 = 2,

x2 = 4 − 4 − 0 = 0.

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.12.2018118.78 Кб10реферат по информатике.doc
#
11.03.201547.7 Кб13Реферат социология.docx
#
01.09.201989.6 Кб14реферат.doc
#
11.03.20157.12 Mб171Реферат.docx
#
06.05.201933.76 Кб62решение 2 задание.docx
#
18.04.2015707.24 Кб34Решение_задач_исследования_операций.pdf
#
11.03.20151.29 Mб143решенные задачи госэкзамен.docx
#
11.03.20154.81 Mб32Роботы.pdf
#
11.03.201526.2 Кб14Романская архитектура германии.docx
#
25.09.201931.3 Кб3Руденко , информатика.docx
#
27.08.2019269.82 Кб2РУП Правовая информатик 2011 специалитет 030501...doc