Вопрос 9. (Обратная матрица)

Матрица А^-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа таки слева – получается единичная матрица. А^-1 *А=А*А^-1 Из определения следует, что только квадратная матрица имеет обратную и обратная матрица так же является квадратной того же порядка.

Теорема №1: Матрица А^-1 существует тогда и только тогда, когда исходная матрица не вырождена, то есть определитель матрицы отличен от нуля. Если определитель равен нулю, то матрица называется вырожденной или особенная.

Теорема №2: Для того, что бы матрица А имела обратную, необходимо и достаточно что бы она была не вырожденной.

Правила нахождения обратной матрицы:

1. Вычислить определитель матрицы А (если А=0 – обратная матрица не существует)

2. Составить матрицу из алгебраических дополнений к элементам матрицы А

3. Транспонировать матрицы (Аij-Aji).

Вопрос 10. (Элементарные преобразования матриц. Ранг матрицы. Вычисление ранга матрицы методом Гауса).

Элементарными преобразованиями матрицы называют следующие операции:

 перестановка любых двух строк матрицы;

 умножение любой строки на произвольное, отличное от нуля, число;

 сложение любой строки с другой строкой , умноженной на произвольное число;

 транспонирование матрицы.

Матрица A^T называется транспонированной по отношению к матрице A= {a_ij}, если A^T= {a_ji}:

Иными словами, матрица, получающаяся из матрицы A  заменой строк столбцами, называется транспонированной по отношению к матрице A и обозначается A^T.

Элементарные преобразования не меняют ранга матрицы.

Наивысший порядок отличных от нуля миноровматрицы называется рангом матрицы.

То есть, если ранг матрицы равен r, то среди миноров матрицы порядка r есть хотя бы один, отличный от нуля, а все миноры матрицы более высоких порядков равны нулю.

Обозначаем Rg A, rg A, rank A.

Ранг матрицы равен максимальному числу линейно независимыхстрок (столбцов) матрицы. То есть, если ранг матрицы равенr, то среди строк (столбцов) матрицы есть r линейно независимых строк (столбцов), а любые r+1 строки (столбца) — линейно зависимы.

Матрицы, имеющие одинаковый ранг — подобные матрицы.

Элементарные преобразования не меняют ранга матрицы.

Ранг ступенчатой матрицы равен количеству ненулевых строк.

Метод Гаусса нахождения ранга матрицы

Пусть дана матрица размеров. Для нахождения ее ранга нужно выполнить следующие действия

1. Привести матрицу к ступенчатому виду (см. метод Гаусса).

2. В полученной матрице вычислить количество ненулевых строк. Это число равно рангу матрицы.

Вопрос 11. (Система линейных алгебраических уравнений слау. Основные понятия)

Совокупность уравнений

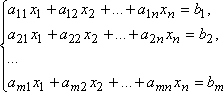
относительная неизвестных x₁, x₂, ..., x_n-1, x_n называется системой линейных алгебраических уравнений.

Числа a_ij — коэффициенты системы, b_i— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.

Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.

Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.

Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.

Если среди правых частей b_i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.

Если все правые части системы равны нулю, то система называется однородной.

Система линейных уравнений может быть записана в матричной форме A·x = b:

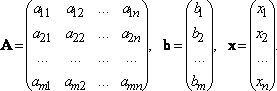
Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.

Иногда удобно записывать систему линейных уравнений в другой матричной форме:

A⁽¹⁾x₁ + A⁽²⁾x₂ + ... + A⁽ⁿ⁾x_n = b. Здесь  A⁽¹⁾, A⁽²⁾, ... , A⁽ⁿ⁾ — столбцы матрицы системы.

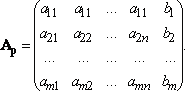
Матрица Ap называется расширенной матрицей системы.

Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.