1.Теория пределов

1.1.Множества на числовой оси

Определение 1. Окрестностью радиуса h > 0 конечной точки x0 или h - окрестностью точки x0

называется множество чисел x , удовлетворяющих неравенству x0 −h < x < x0 +h , т. е. множество

(x0 − h; x0 + h) (рис. 1).

Обозначается: Uh (x0 ) .

Рис. 1.

Если x Uh (x0 ) , то x удовлетворяет неравенству

x − x0 < h − h < x − x0 < h x0 − h < x < x0 + h .

Расширим систему вещественных чисел, добавив к ним два символа −∞ и + ∞ , которые назовём бесконечно-удалёнными точками числовой оси. Определим для этих точек следующие свойства:

1) Если x R и является конечным числом, то

x + ∞ = +∞ ; x −∞ = −∞ ; −x∞ = +x∞ = 0 ;

2)Если x > 0 , то x (+∞) = +∞ , x (−∞) = −∞ ;

3)Если x < 0 , то x (+∞) = −∞ , x (−∞) = +∞ ;

Определение 2. Пусть h > 0 . h -окрестностью точки (+∞) называется множество чисел x , удовлетворяющих неравенству x > h , т. е. множество (h; + ∞) (рис. 2). Обозначение: Uh (+∞) .

Рис.2.

Тогда x Uh (+∞) x > h .

Определение 3. Пусть h > 0 h -окрестностью точки (−∞) называется множество чисел x , удовлетворяющих неравенству x < −h , т. е. множество (−∞; − h) (рис. 3). Обозначение: Uh (−∞) .

Рис. 3.

Тогда x Uh (−∞) x < −h .

Определение 4. Пусть h > 0 . Проколотой h -окрестностью точки x0 называется множество чисел

•

x Uh (x0 ) и x ≠ x0 (рис. 4). Обозначение: U h (x0 ) .

если в любой проколотой окрестности точки x0 находится хотя бы один элемент данного множества X .

Можно показать, что в любой окрестности точки сгущения находится бесконечное множество

элементов множества X .

Точка сгущения может принадлежать множеству, но может ему и не принадлежать. Например, для множеств (1; 2) и [1; 2] точки 1 и 2 являются точками сгущения.

2

Определение 6. Точка, принадлежащая множеству и не являющаяся его точкой сгущения, называется изолированной. Например, во множестве натуральных чисел {n} каждая конечная точка является

изолированной. Множество имеет единственную предельную точку x0 = +∞ . Действительно, в любой

•

lim f (x) = A Uε ( A) Uδ (x0 ) : x Uδ (x0 ) ∩ X f (x) Uε ( A) .

x→x0

Если известно, что x0 и A - конечные или бесконечные числа, то можно дать определение предела

•

без использования понятия окрестности. При этом записи x Uδ (x0 ) и f (x) Uε ( A) следует заменить соответствующими неравенствами.

Рассмотрим некоторые случаи значений x0 и A .

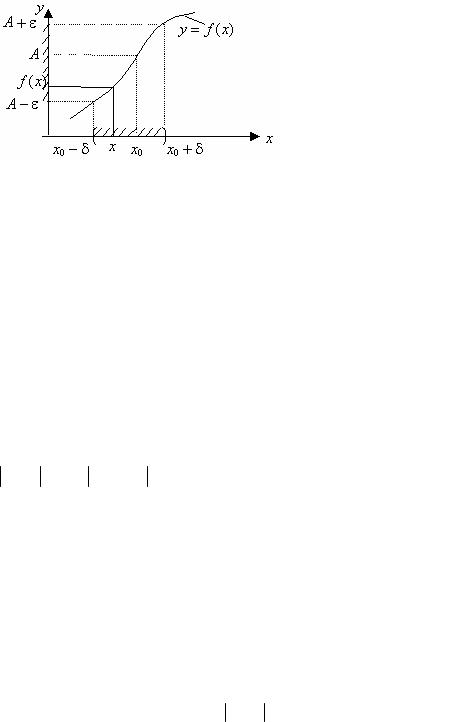
1). Пусть x0 , A - конечные числа (рис. 6) lim f (x) = A ε > 0 δ(ε) > 0 : x X и

x→x0

0 < x − x0 < δ f (x) − A < ε.

ε > 0 δ(ε) > 0 : x X и 0 < x − x0 < δ f (x) > ε (рис. 7).

3

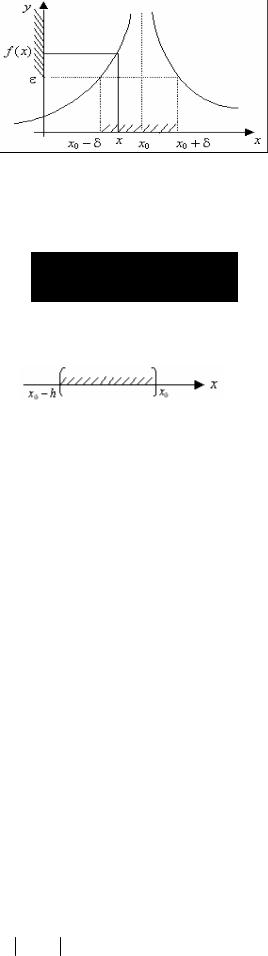
Рис. 7.

1.3. Односторонние пределы. Предел последовательности

Определение 1. Пусть h > 0 . Правосторонней h -окрестностью точки x0 называется множество точек x : x (x0 ;h + x0 ) , где h > 0 (рис. 8).

Рис. 8.

Левосторонней h -окрестностью точки x0 называется множество точек x : x (x0 − h; x0 ) ,где h > 0 (рис. 9).

Рис. 9.

Правая и левая окрестности обозначаются: Uh+ (x0 ) и Uh−(x0 ) соответственно.

Определение 2 (Правостороннего предела).

A = lim f (x) Uε ( A) Uδ(x0 ) : x Uδ+ (x0 ) ∩ X f (x) Uε ( A) .

x→x0 +0

Определение 3 (Левостороннего предела).

A = lim f (x) Uε ( A) Uδ (x0 ) : x Uδ− (x0 ) ∩ X f (x) Uε ( A) .

x→x0 −0

ЗАМЕЧАНИЕ

Из определений ясно, предел в конечной точке существует только тогда, когда оба односторонних предела в этой точке существуют и они равны между собой.

ЗАМЕЧАНИЕ

Для точек x0 = ±∞ понятие окрестности совпадает с понятием правосторонней или левосторонней

окрестности. Поэтому lim f (x) совпадает с соответствующим право-(или лево) сторонним пределом x→±∞

функции.

Поскольку последовательность – это функция натурального аргумента, то единственной точкой сгущения области определения числовой последовательности является точка + ∞ . Поэтому предел последовательности может быть определен только при аргументе n → ∞.

Определение 4 (Предел числовой последовательности).

lim xn = A Uε ( A) число M N : n > M xn Uε ( A) .

n→∞

При этом, если A - конечное число, то определение предела можно записать в виде: ε > 0 M N : n > M xn − A < ε .

4

f( y) ,

3)существует lim f ( y) = B ,

→Ay

то существует lim f (g(x)) = B .

x→x0

5