
- •2. Векторная алгебра (4 часов).
- •2. Векторная алгебра
- •2.1 Векторы в пространстве
- •2.3 Задачи, решаемые с помощью скалярного произведения
- •2.4 Направляющие косинусы
- •2.5 Коллинеарные векторы
- •2.6 Векторное произведение и его свойства
- •2.7 Смешанное произведение векторов и его свойства
- •2.8 Геометрический смысл векторного произведения
- •2.9 Задачи, решаемые с помощью векторного произведения
- •2. Векторная алгебра (4 часа).
- •Основная
- •Дополнительная

r |
r r |
образуют правую тройку, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3. Векторы a,b ,c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
так как ar br cr = ([ar,br],cr)= ([ar,br],[ar,br])= |
|
[ar,br] |
|
2 > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
[ar,br] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
[ar,b ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Рис. 2.11. |
|
|
|
|
|
|
|
|
|
|
br |
|
|
|
|
|
||||||||||
Пример 1. Найти |
|
[cr ,cr |
] |
|
, если cr = 4ar −2b и cr = −ar +3b . |
|
|
ar |
|
= |
|
|
|
|
|
= 2 , ar b = 30o . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
1 |
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. По свойствам векторного произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
[cr1 ,cr2 ]= [4ar −2br,−ar +3br |
]= −4[ar,ar]+ 2[b ,ar]+12[ar,b]−6[b ,b ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Учитывая, что [ar, ar]= 0r, [br, br]= 0r и [ar,b]= −[b ,ar], получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
[cr1 ,cr2 ]= −2[ar,br]+12[ar,br]=10[ar,br]. Тогда |
|
[cr1 ,cr2 ] |
|
=10 |
|
[ar,br] |
|
|
=10 |
|
ar |
|
|
|
br |
|
sin(ar br)= |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=10 2 2 sin 30o = 40 0,5 = 20 .
Ответ. [cr1 ,cr2 ] =20.
2.9Задачи, решаемые с помощью векторного произведения
1.Вычисление площадей параллелограмма и треугольника, построенных на двух векторах.
a
 α
α
b
Рис. 2.12
Площадь параллелограмма, построенного на векторах a и b равна |
|
|
|||||||||||||||||||||||||
Sпар = |
|
ar |
|
|
|
br |
|
sin(ar br), а площадь треугольника Sтр |
|
=1 2 Sпар =1 2 ar br sin(ar br). |
|||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
Из условия |
|
2 |
|
пункта 2.8 следует Sпар = [ar,br], Sтр =1 2 |
|
[ar,br] |
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
Пример 1. Вычислить площадь треугольника |
ABC , |
|
если |
A(2,− 2,3), |
B(−3,− 6,0), |
||||||||||||||||||||||
C(4,−3,−1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Треугольник АВС образован векторами |
kr |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
−5 |
|
|
|
|
|
2 |
[AB, AC]= |
|
ir |
rj |
|
r |
r |
r |
13 |
|
|||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
− 4 |
|
|
|
|
|
−1 |
|
|
−5 − 4 |
−3 |
|
|
|
|||||||||||||
AB = |
|
и |
AC = |
. |
|
|
=13i |
−26 j |
+13k |
= − 26 |
. |
||||||||||||||||
|
−3 |
|
|
|
|
|
− 4 |
|
|
|
2 −1 − 4 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|||||||||
S ABC =1 2 [AB, AC] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
=1 2 |
132 + 262 +132 |
=13 2 |
6 . |
|
|
|
|
|
|
|
|
||||||||||||||||
Ответ. 13 2 |
6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
18

2. Вычисление момента сил. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если вектор силы |
fr |
приложен к точке A и требуется найти момент этой силы |
|
|
|||||||||||||
относительно точки О, то момент силы M равен M = [OA, f ](рис.2.13). |
|
|
|
|
|
||||||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
fr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.13. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
r |
−1 |
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить |
|
|
|
|
|
|
|
|
|
|
|
A(3,− 2,7) |
|||||
момент силы |
|
f = 2 |
, |
приложенной |
к |
точке |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно точки O(−1,2,1). |
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
||||
|
ir |
rj |
kr |
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
r |
r |
|
r |
|
−18 |
||||||
|
|
|
|
|
|||||||||||||
|
|
− 4 |
|
|
4 |
− 4 |
6 |
|
+ |
|
− |
12 |
|
||||
Решение. OA = |
, M = [OA, f ]= |
|
|
= −18i |
−12 j |
4k |
= |
. |
|||||||||
|
|
6 |
|
|
|
−1 |
2 |
1,5 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
−18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
−12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. M = |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Определение вектора, ортогонального двум данным
Иногда требуется найти вектор, ортогональный двум данным. Из условия 1 пункта 2.8 следует, что искомый вектор коллинеарен векторному произведению заданных векторов.
Пример 3. Найти вектор p , ортогональный векторам,
|
1 |
|
r |
−7 |
(p,c)= 3 |
1 |
|||
ar |
|
2 |
|
|
0 |
|
|
||
= |
и b |
= |
, для которого |
, где c = 1 . |
|||||
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
||
Решение. |
Вектор |
p коллинеарен векторному произведению [ar,b ], следовательно |
|||||||
p =α [ar,br].
Поскольку [ar |
|
r |
]= |
|
ir |
rj |
kr |
|
r |
r |
|
r |
|
4 |
|
|
|
|
|
|
|||||||||||||
|
|
1 |
2 |
3 |
|
+ |
|
|
|
|||||||
,b |
|
|
= 4i |
− 23 j |
14k |
= |
− 23 , то |
|||||||||
|
|
|
|
|
|
−7 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
||||
|
4 |
|
|
|
4α |
|
|
|
|
|
|
|
|
|
|
|
|
− 23 |
|
|
|
|
|
|
|
|
|
|
|
|
4α 1 − 23α 1 +14α 1 = 3 , |
||
p =α |
|
= |
− 23α . Так как (p,cr)= 3 , то |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
14α |
|
|
|
|
|
|
|
|
|
|
|||
или −5α = 3,α = −3 5 = −0,6 . Теперь можно определить координаты вектора p :
5 = −0,6 . Теперь можно определить координаты вектора p :
19
4 |
|
− 2,4 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p = α − 23 |
|
= 13,8 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14 |
|
−8,4 |
|
|
|
|
|
|
|
|
|||||||||
|
|
− 2,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ. p = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13,8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
−8,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.10 |
Геометрический смысл смешанного произведения. Задачи, |
||||||||||||||||||
|
|
|
|
|
решаемые с помощью смешанного произведения |
||||||||||||||
arbrcr = ([ar,br],cr)= |
|
[ar,br |
] |
|
|
|
cr |
|
cosα , где α - угол между векторами |
[ar,b ]и c . |
|||||||||
|
|
|
|
||||||||||||||||
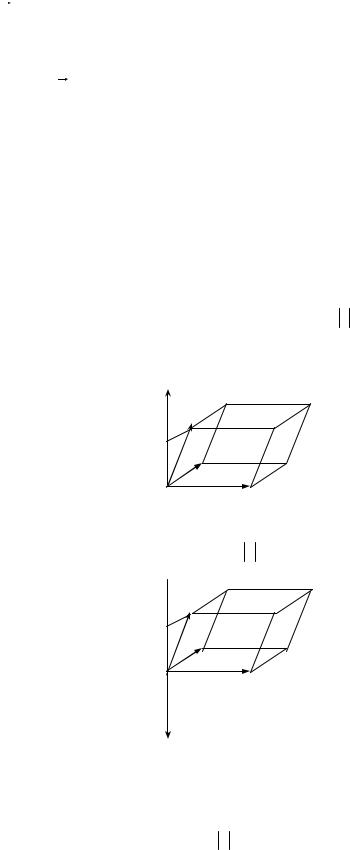
Построим на векторах |
ar,b ,cr параллелепипед (рис. 2.14.) |
и покажем, что смешанное |
|||||||||||||||||
произведение arbrcr равно модулю объема этого параллелепипеда. |
Так как |
|
[ar,br] |
|
равно |
||||||||||||||
|
|
||||||||||||||||||
площади параллелограмма, построенного |
на векторах ar,b |
или |
площади основания |
||||||||||||||||
параллелепипеда, |
построенного на векторах |
ar,b ,cr, а cr cosα – проекция вектора cr на |
|||||||||||||||||
вектор [ar,br]или высота h параллелепипеда, то arb cr = Sпар−ма h =Vпараллелепида .
[ar,br]
cr
h α b
a
Рис. 2.14.
Рис. 2.14. сделан для векторов, которые образуют правую тройку, в этом случае угол между векторами cr и [ar,br]острый и h = cr cosα > 0 .
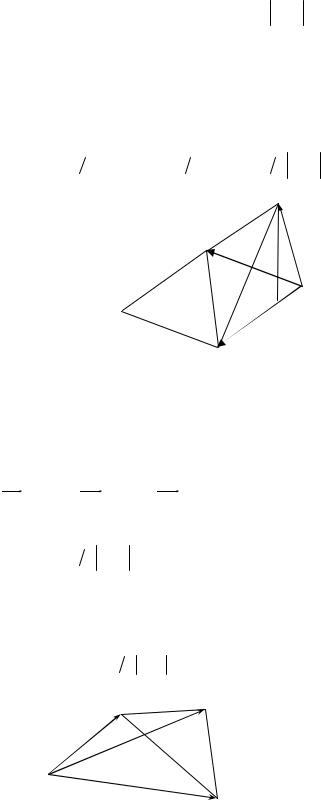
c h α b
a
[ar,br]
Рис. 2.15.
r r r [r r]
Если тройка векторов a,b ,c – левая (рис.2.15.), то угол между векторами c и a,b >90o. В этом случае cosα < 0 и тогда h = −cr cosα > 0 . Поэтому arb cr = −Vпараллелепида . При любом расположении векторов arb cr = ±Vпараллелепида .
20
Геометричеcкий смысл смешанного произведения используют при вычислении объемом параллелепипедов и тетраэдров, построенных на трех векторах. Формула объема
параллелепипеда уже получена Vпараллелепида = arbrcr .
Выведем формулу объема тетраэдра (четырехугольной пирамиды), построенной на
векторах ar,br,cr. Из рис. 2.16 легко видеть, чтоVтетраэдра =1 3 S0 h , где S0 - площадь треугольника в основании тетраэдра, а h – его высота. Поскольку площадь треугольника
3 S0 h , где S0 - площадь треугольника в основании тетраэдра, а h – его высота. Поскольку площадь треугольника
S0 =1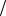 2 Sпар−ма , где Sпар−ма – площадь параллелограмма, построенного на векторах a и b ,
2 Sпар−ма , где Sпар−ма – площадь параллелограмма, построенного на векторах a и b ,
а высоты тетраэдра и параллелепипеда, построенных на векторах ar,b ,cr совпадают, то
Vтетраэдра =1 6 Sпар−ма h =1 6 Vпар−да =1 6 arbrcr .
c
b h
a
Рис. 2.16.
Пример. Найти объем тетраэдра ABCD , если A(1,−3,−5), B(−1,2,− 4), C(0,0,− 2),
D(− 6,−1,− 2).
Решение. |
Тетраэдр ABCD построен на векторах |
||||||
− 2 |
|
|
−1 |
−7 |
|
||
|
|
|
3 |
|
|
2 |
|
AB = 5 |
, AC = |
, AD = |
, (Рис. 2.17). |
||||
|
|
|
3 |
|
|
3 |
|
1 |
|
|
|
|
|
||
|
|
|
r r r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Vтетраэдра =1 6 a b c . Вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
r r r |
|
− 2 |
5 |
1 |
|
(−3) (−3) |
|
|
− 2 |
5 |
1 |
|
|
5 |
−12 |
|
= (−13 |
|
−12)= −77 . |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
−1 |
3 |
3 |
|
|
|
= |
|
5 −12 |
0 |
|
= |
|
5 |
||||||
a b c = = |
|
|
|
|
|
−1 |
−13 |
|
||||||||||||
|
|
− 7 |
2 |
3 |
|
|
|
|
|
−1 |
−13 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда Vтетраэдра =1 6 −77 = 77 / 6 .
Ответ. 77 / 6 . D
C
A
B
Рис. 2.17.
21
