Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный морской технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

razdel_2_konspekta_lektsy.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

626.88 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 154 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Решение

Областью определения функции является множество (0 + ∞) , для которого 0 есть

предельная точка. Покажем, что

ε > 0

δ(ε) > 0 : 0 < x < δ log2 x < −ε (рис. 2.11).

(

)

− ε)

Рис. 2.11.

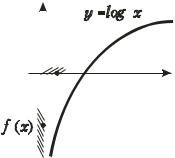
На рисунке 2.11 изображен график

функции у = log2 x

проиллюстрировано

определение предела.

Рассмотрим равносильные неравенства

log2 x < −ε 0 < х< 2−ε .

Если взять δ(ε) = 2−ε , то будет выполнено:

ε > 0 δ(ε) = 2−ε : 0 < x < δ = 2−ε log2 x < −ε ,

а это и доказывает, что

lim

log2 x = −∞.

x→0−0

2.1.4. Основные теоремы о пределах

Теорема 2.1.1. (Единственность предела)

Если функция f (x)

имеет предел при x → x0 , то он единственный.

Доказательство. (От противного)

Пусть lim f (x) = A

и lim f (x) = B . Тогда по определению конечного предела

x→x0

f (x) − B < ε .

ε > 0 Uδ(x0 ) : x U δ(x0 ) ∩ X f (x) − A < ε и

•

Найдём

A − B

A − B + f (x) − f (x)

( A − f (x)) + ( f (x) − B)

≤

A − f (x)

f (x) − B

f (x) − A

f (x) − B

= ε

A − B

< ε

ε > 0 . Поскольку модуль – число

Получили, что

не

отрицательное,

то

неравенство

A − B

< ε

ε > 0 может быть выполнено только в случае A − B = 0 , т. е.

при A = B .

Теорема 2.1.2. (Предельный переход в неравенстве)

Если в некоторой окрестности точки

выполняется неравенство f (x) ≤ g(x)

существуют конечные пределы lim f (x) = A

и lim g(x) = B , то A ≤ B .

x→x0

Доказательство

Пусть X ― общая область определения функций определению предела функции

f (x) и g(x)

. Тогда по

•

lim f (x) = A ε > 0 Uδ1 (x0 ) : x U δ1 (x0 ) ∩ X f (x) − A < ε ,

x→x0

lim g(x) = B ε > 0 Uδ

•

(x0 ) ∩ X

g(x) − B

(x0 ) : x U δ2

< ε.

x→x0

Если в обоих случаях взять одно и то же ε > 0 и из найденных окрестностей Uδ1

(x0 )

и Uδ2

(x0 )

выбрать

наименьшую,

т.

е.

Uδ(x0 ) =Uδ1 (x0 ) ∩Uδ2 (x0 ) ,

то

для

•

(xо) ∩ X выполняются оба неравенства одновременно, т. е.

x U δ

A −ε < f (x) < A + ε, B −ε < g(x) < B + ε.

Выберем ε =

A − B

, предположив противное, т. е. пусть A > B . Тогда

A − B

A + B

3A − B

−

< f (x) < A

< f (x) <

A − B

3B − A

< g(x) <

A + B

−

< g(x) < B

g(x) <

A + B

< f (x) ,

из последнего неравенства следует,

что

g(x) < f (x) ,

что противоречит

условию

теоремы, значит наше предположение

A > B

неверно. Тогда

верным

является

неравенство A ≤ B .

Теорема 2.1.3. (Предел суперпозиции, т. е. сложной функции)

Если:

1) f ( y) и g(x) таковы, что можно образовать их суперпозицию F(x) = f (g(x)) ,

существует

lim g(x) = A , точка

A -

является

точкой

сгущения

области

x→x0

определения функции

f ( y) ,

3) существует lim f ( y) = B ,

y→A

то существует lim

f (g(x)) = B .

x→x0

Доказательство

Пусть X – область определения функции g(x) ,

Y – область определения функции

f ( y) . По определению предела функции

•

lim

g(x) = A U h ( A) Uδ(xo ) : x Uδ(x0 )

∩ X g(x) U h

( A) ,

x→x0

•

lim

f ( y) = B Uε (B) U h

( A) : y U h2 ( A)

∩Y f ( y) Uε (B) .

y→A

Возьмём h = min {h1; h2 }. Тогда получим

•

Uε (B) Uδ(xo ) : x U δ(xo ) ∩ X f (g(x)) Uε (B) .

Значит, по определению предела функции B = lim

f (g(x)) .

x→x0

Теорема 2.1.4. (О сжатой функции)
Если в некоторой	окрестности	точки x0	три функции	связаны неравенством
ϕ(x) ≤ f (x) ≤ g(x) и	существуют	конечные	пределы lim ϕ(x) = lim g(x) = A , то
			x→x0	x→x0

существует lim f (x) = A.

x→x0

Доказательство

Пусть X - общая область определения трёх функций, тогда

•

lim ϕ(x) = A Uε ( A) Uδ1 (x0 ) : x U δ1 (x0 ) ∩ X ϕ(x) − A

x→x0

lim	g(x) = A U	ε ( A) Uδ		•	(x0 ) ∩ X		g(x) − A
lim	g(x) = A U	ε ( A) Uδ	(x0 ) : x U δ2		(x0 ) ∩ X		g(x) − A
x→x0		2
Найдём	окрестность	Uδ(x0 ) =Uδ		(x0 ) ∩Uδ		(x0 ) ,	тогда
			1		2

•

x U δ(x0 ) ∩ X выполняются оба неравенства одновременно:

<ε,

<ε .

для

A −ε < ϕ(x) < A + ε и A −ε < g(x) < A + ε.

Но так как ϕ(x) ≤ f (x) ≤ g(x) , то A −ε < ϕ(x) ≤ f (x) ≤ g(x) < A + ε, а это означает,

что существует lim f (x) = A.

x→x0

Теорема 2.1.5. (Первый замечательный предел)

Сначала докажем, что при 0 < x <	π	выполняется неравенство		.
			sin x < x < tg x
	2

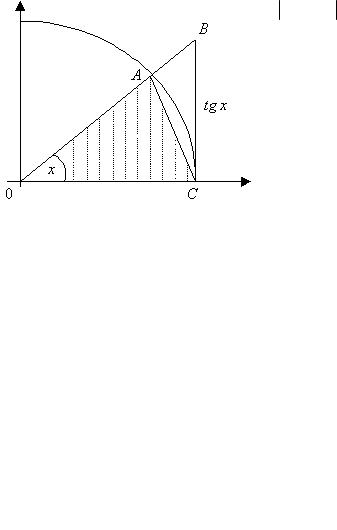
Возьмём Ι четверть тригонометрического круга и отложим угол x радиан (рис. 2.12).

											Рис. 2.12.
Очевидно,			что				S OAC < Sсек.OAC < S OBC ,					найдём эти					площади,					зная, что		радиус
окружности равен 1.
				1								1									1	R2 x =	1
S OAC			=	1		OA		OC sin(OA ; OC) =				1		1 1 sin x , Sсек.OAC =							1		1	x ,
S OAC			=	2		OA		OC sin(OA ; OC) =				2		1 1 sin x , Sсек.OAC =							2		2	x ,
				2								2									2		2
							S OBC =			1	OC BC =		1		1	tg x =	1		tg x .
							S OBC =				OC BC =				1	tg x =	2		tg x .
								2				2					2
Значит,	1	sin x <			1		x <	1	tg x sin x < x < tg x							x (0;			π	) .
Значит,		sin x <		2			x <	2	tg x sin x < x < tg x							x (0;		2		) .
2				2				2										2

Теперь докажем, что

<<< < Предыдущая 1 2 34 / 154 5 6 7 8 9 10 11 12 13 14 15 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015717.31 Кб37rabota_po_Boroviikovo_2012_Poslednyaya.doc
#
09.12.20181.45 Mб37RadioMeasurements.docx
#
23.11.20181.23 Mб17Raschet_kriticheskogo_polozhenia.doc
#
18.04.2015454.14 Кб12rastvory_metodichka.doc
#
18.04.2015993.48 Кб49razdel_1_konspekta_lektsy.pdf
#
18.04.2015626.88 Кб73razdel_2_konspekta_lektsy.pdf
#
18.04.2015972.79 Кб76razdel_3_konspekta_lektsy.pdf
#
01.03.2025110.59 Кб0ref-16579.doc
#
18.04.201535.79 Кб27Referat_1.docx
#
18.04.2015194.49 Кб6Rhtlbngjhnatkm.docx
#
18.04.2015228.19 Кб9Sankt.docx

Решение

2.1.4. Основные теоремы о пределах

Теорема 2.1.1. (Единственность предела)

Доказательство. (От противного)

Теорема 2.1.2. (Предельный переход в неравенстве)

Доказательство

Доказательство

Теорема 2.1.4. (О сжатой функции)

Доказательство

Теорема 2.1.5. (Первый замечательный предел)