Доказательство |
|
|
|
|
|
|
Найдем |
|
|
|
|
|
|
lim F(x) = lim (f (x) + g(x))= lim |
f (x) + lim g(x) = f (x0 ) + g(x0 ) = F(x0 ) |
|||||
x→х0 |
x→х0 |
|
|
x→х0 |
x→x0 |
|
функция F(x) = f (x) + g(x) |
― непрерывная в точке x0 . Аналогично доказываются |
|||||
теоремы для произведения и частного. |
|
|
||||
Теорема 2.2.1 |
|
|
|
|
|
|
Если функция g(x) |
непрерывна в точке x0 , а функция |
f (u) ― в точке u0 = g(x0 ) , |
||||
то сложная функция f (g(x)) непрерывна в точке x0 . |
|
|||||
Доказательство |
|
|
|
|
|
|
|
|
lim f (g(x)) = lim |
f (u) = f (u0 ) = f (g(u0 )) . |
|||
|
x→х0 |
|
u→u0 |
|
|
|
Определение 2.2.4 |
|
|
|
|
|
|
Функция y = f (x) |
называется непрерывной слева (справа) в точке x0 , если она |
|||||
определена в точке x0 |
и |
lim |
f (x) = f (x0 ) (или lim |
f (x) = f (x0 ) ). |
||
|
|
x→х0 −0 |
|
x→х0 +0 |
|
|
2.2.2. Классификация точек разрыва |
|
|
||||
Если функция |
f (x) |
не является непрерывной в точке x0 , то говорят, что она терпит в |
||||
этой точке разрыв.
Чтобы классифицировать точки разрыва функции дадим определение непрерывной в точке функции в развернутом виде.
Функция f (x) называется непрерывной в точке x0 , если:
1)f (x) определена в некоторой окрестности точки x0 ;Устранимый разрыв
2)существуют конечные односторонние пределы
lim f (x) = f (x0 − 0) и |
lim f (x) = f (x0 + 0) ; |
|
x→x0 −0 |
|
x→x0 +0 |
3) эти пределы равны значению функции в точке x0 , т.е. |
||
lim |
f (x) = lim |
f (x) = f (x0 ) . |
x→х0 −0 |
x→х0 +0 |
|
Если в точке x0 хотя бы одно из условий непрерывности нарушается, точка x0 является точкой разрыва данной функции.
1. Устранимый разрыв
Пусть существуют конечные односторонние пределы:
lim f (x) = f (x0 − 0) и |
lim |
f (x) = f (x0 + 0) . |
x→x0 −0 |
x→x0 +0 |
|
Если А= f (x0 − 0) = f (x0 + 0) ≠ f (x0 ) , то точка |
x0 называется точкой устранимого |
|
разрыва (рис. 2.1).
у
А= f (хо- 0) =
= f (хо+ 0)
|
|
|
х |
0 |
хо |
||
|
Рис. 2.1. |
|
|
23
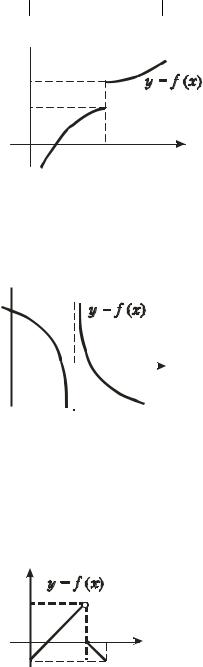
Для того, чтобы устранить разрыв, нужно доопределить (или переопределить) функцию в самой точке x0 , т.е. ввести новую функцию
f (x), если х ≠ x0 |
. |
||
у = |
|
х = x0 |
|
А, |
если |
|
|
2. Неустранимый разрыв первого рода |
|
|
|
Пусть существуют конечные односторонние пределы: |
|
||
lim f (x) = f (x0 − 0) |
и |
lim f (x) = f (x0 + 0) . |
|
x→x0 −0 |
x→x0 +0 |
|
|
Если f (x0 − 0) ≠ f (x0 + 0) , то точка x0 |
называется точкой неустранимого разрыва |
||
первого рода (рис. 2.2). Величина δ = f (x0 + 0) − f (x0 − 0) называется скачком функции f (x) в точке x0 .
у
f (хо+ 0) f (хо- 0)
0 |
хо |
х |
|
Рис. 2.2. |
|
3. Неустранимый разрыв второго рода
Если в точке x0 хотя бы один из односторонних пределов не существует или равен
∞, то точка x0 называется точкой неустранимого разрыва второго рода (рис. 2.3).
у
|
|
0 |
|
|
хо |
|
|
х |
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.3. |
|
|
||
Задача 2.2.1 |
|
|
|
|
|
|
|
|
Исследовать функцию |
|
x −1, |
если 0 ≤ х < 3, |
на непрерывность: |
||||
f (x) = |
3 − х, |
если |
3 ≤ х ≤ 4. |
|||||
|
|
|
|
|
||||
Решение
Изобразим график этой функции (рис. 2.4).
у |
|
2 |
|
0 |
3 4 |
- 1 |
х |
|
|
|
Рис. 2.4. |
Для функции f (x) точка х = 3 является точкой разрыва первого рода, так как
24
lim |
f (x) = |
lim |
(x |
−1) |
= 2 |
|
x→3−0 |
|
x→3−0 |
|
|
|
разрыв первого рода, скачок δ = 2 . |
lim |
f (x) = |
lim |
(3 |
|
|
|
− x) = 0 |
|
|||||
x→3+0 |
|
x→3+0 |
|
|
|
|
Следует отметить, что в точке х = 0 функция непрерывна справа, так как
|
lim |
f (x) = |
lim (x −1) = −1 = f (0) . |
||
|
x→0+0 |
|
|
x→0+0 |
|
А в точке х = 4 функция непрерывна слева, так как |
|||||
|
lim |
f (x) = |
lim (3 − x) = −1 = f (4) . |
||
|
x→4−0 |
|
|
x→4−0 |
|
Задача 2.2.2 |
|
|
|
|
|
Исследовать функцию |
y = |
sin x |
на непрерывность. |
||
|
|||||
|
|
x |
|
|
|
Решение
Функция f (х) не определена в точке x = 0 . Эта точка является точкой устранимого разрыва, так как
lim |
sin x |
= |
lim |
sin x |
=1 . |
|
x |
x |
|||||
x→0−0 |
|
x→0+0 |
|
у
1
|
|
|
|
0 |
х |
|
|
|
|
Рис. 2.5. |
|
График функции |
y = |
sin x |
изображен на рисунке 2.5. |
|
|
|
|
||||
|
|
|
x |
|
|
Доопределить функцию по непрерывности – это значит задать f (0) =1 , т.е. получить
sin x |
, x |
≠ 0 |
|
|
|
|||
|
x |
x = 0 . |
||||||
функцию y = |
|
, которая непрерывна в точке |
||||||
|
x = 0 |
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
||
Задача 2.2.3 |
|
|
|
|
|
|
|
|
Исследовать функцию y = sin |
1 |
на непрерывность. |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
Точка x = 0 |
является точкой разрыва второго рода, так как пределы lim sin |
1 |
не |
|||||
x→0±0 x
существуют.
у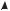
0 |
х |
|
Рис. 2.6.
25