1) |
если |
lim |
U (x) |
= ∞, |
то U (x) называется б.б. высшего порядка относительно |
||||||||
|
|
|
|||||||||||
|
x→x0 |
V (x) |
|
|
|
|
|
|
|
||||
V (x) , а V (x) – б.б. низшего порядка относительно U (x) . Очевидно lim |
V (x) |
= 0 . |
|
||||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x→x0 |
U (x) |
|
|
2) |
если |
lim |
|
U (x) |
= C , |
где |
C ≠ 0, C ≠ ∞ , то U (x) и V (x) называются |
б.б. |
|||||
|
V (x) |
||||||||||||
|
|
x→x0 |
|
|
|
|
|
|
|
||||
одинакового порядка. |
|
|
|
|
|
|
|
||||||
3) |
если / |
lim |
U (x) |
, то U (x) |
и V (x) называются несравнимыми. |
|
|
|
|||||
|
|
|
|
|
|||||||||
|
|
x→x0 |
V (x) |
|
|
|
|
|
|||||
4) |
если |
lim |
|
U (x) |
=1 , |
то U (x) и V (x) называются эквивалентными б.б. |
что |
||||||
|
V (x) |
||||||||||||
|
|
x→x0 |
|
|
|
|
|
|
|
||||
обозначается: U (x) ~ |
|
V (x) . |
|
|
|
|
|||||||
|
|
|
|
|
x→x0 |
|
|
|
|
|
|||
Свойства эквивалентных б.б. функций
1)Сумма б.б. функций разного порядка эквивалентна б.б. высшего порядка.
2)Предел отношения б.б. не изменится, если числитель и знаменатель заменить на
эквивалентные б.б. Иначе: если U (x) ~ U1 (x) |
и V (x) ~ V1 (x) , x → x0 , то |
|||||
lim |
U (x) |
= |
lim |
U1 (x) |
. |
|
V (x) |
V1 (x) |
|||||
x→x0 |
|
x→x0 |
|
|||
3) Сумма б.б. функций можно заменить на сумму эквивалентных б.б., если заданная сумма не является разностью эквивалентных б.б.
4) Если U (x) ~ U1(x) и V (x) ~ V1(x) , x → x0 , то U (x) V (x) ~ U1(x) V1(x) .
2.1.9. Главная часть б.м. и б.б. функций
Для каждой б.м. или б.б. функции существует бесконечное множество эквивалентных функций. Например, при x → 0 б.м. функция tg x ~ sin x; ~ arcsin x; ~ x и т. д.
Естественно при вычислении пределов использовать замену на простейшую эквивалентную функцию.
Определение 2.1.14
Пусть α(x) |
– простейшая |
б.м. в точке x0 , а β(x) – другая б.м. в той же точке x0 . |
|
Если β(x) |
~ |
C(α(x))k , где |
C, k – постоянные числа, C ≠ 0 , то бесконечно малую |
|
x→x0 |
|
|
C(α(x))k |
называют главной частью β(x) . Число k называют порядком функции β(x) |
||
относительно α(х) .
18
ЗАМЕЧАНИЕ
Вид главной части зависит от того, конечным или бесконечным является число x0 . Пусть
β(x) – б.м. в точке x0 , то |
|
|
|
|
|
1) Если x0 |
= a – конечное число, то главная часть функции β(x) |
имеет вид C (x − a)k . |
|||
|
|
β(x) |
1 |
k |
|
2) Если x0 |
= ∞, то главная часть функции |
имеет вид C |
|
. |
|
|
|||||
|
|
|
x |
|
|
Определение 2.1.15
Пусть U (x) – простейшая бесконечно большая в точке x0 , V (x)
большая в той же точке x0 . Если V (x) ~ C(U (x))k , где C, k x→x0
–другая бесконечно
-постоянные числа,
C ≠ 0 , k > 0 , то бесконечно большую |
C(U (x))k называют главной частью |
V (x) . |
|||
Число k называют порядком V (x) относительно U (х) . |
|
|
|
||
ЗАМЕЧАНИЕ. |
|
|
|
|
|
Пусть V (x) – б.б. в точке x0 . Тогда: |
|
|
|
|
|
1) если x0 |
= a – конечное число, то главная часть функции V (x) имеет вид |
1 |
k |
||
C |
|
. |
|||
|
|||||
|
|
|
x − a |
||
2) если x0 |
= ∞, то главная часть функции V (x) имеет вид C (x)k . |
|
|
|
|
Задача 2.1.8 |
|
|
|
|
|
Выделить |
главную часть функции |
f (x) = cos x − e3x при x → 0 и |
установить ее |
||
порядок относительно х. |
|
|
|
|
|
Решение |
|
|
|
|
|
lim (cos x − e3x )= 0 . Следовательно, |
функция f (x) является бесконечно малой и ее |
||||||||
x→0 |
|
|
|
|
|
|
|
|
|
главная часть при x → 0 имеет вид C (x − 0)k |
= С хk , где k – порядок функции f (x) |
||||||||
относительно |
х. |
Воспользуемся |
|
|
соотношениями |
|
|
эквивалентностей |
|
1 −cos α(х) ~ |
(α( х) )2 |
и eα( х) −1 ~ α(х) , для этого приведем |
f (x) к виду |
||||||
2 |
|||||||||
α( x)→0 |
|
α( x)→0 |
|
|
|
|
|
|
|
f (x) = cos x − e3x = cos x − e3x ±1 = −(1 − cos x) − (e3x −1) ~ |
− |
1 |
x2 − 3x . |
||||||
|
|||||||||
|
|
|
|
|
|
x→0 2 |
|||
Меньший порядок имеет слагаемое (−3х), поэтому |
|
|
|
||||||
|
|
f (x) = cos x − e3x |
~ |
− |
1 |
x2 − 3x ~ − 3х. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
x→0 |
2 |
x→0 |
|
|
|
|
Главная часть функции f (x) имеет вид − 3х1 , где k =1 – ее порядок относительно х.
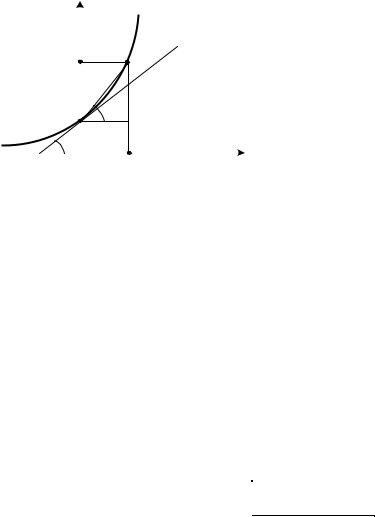
Определение 2.1.16 |
|
Числом «е» называют основание такой показательной |
функции f (x)= ax , |
касательная к графику которой, проведенная в точке с абсциссой x0 |
= 0 , составляет угол |
α = 45o с осью абсцисс (рис. 2.13). |
|
19
|
|
|
|
|
|
|
|
y |
|
|
|
|
}ex −1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
ex |
|
β |
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
1 x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рис. 2.13. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из определения следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
tgβ = |
ex |
−1 |
, limtgβ = lim |
ex −1 |
= tgα = tg45 |
o |
=1 (рис. 2.13). |
|||||||||||
|
x |
|
x |
|
|
|
||||||||||||
|
|
x→0 |
|
x |
→0 |
|
|
|
|
|
|
|
|
|||||
|
|
ex −1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, lim |
= |
=1 |
|
e |
x |
−1 ~ x |
. |
|
|
|
||||||||
x |
|
|
|
|
|
|
|
|||||||||||
x→0 |
|
|
0 |
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выяснено, что e ― это иррациональное число (оно называется числом Непера). |
Это |
|||||||||||||||||||||||||||||||||||||||||||||
число |
вычислено |
|
e 2,7182818284... Натуральными |
называются логарифмы, |
|
|
за |
|||||||||||||||||||||||||||||||||||||||
основание которых принято число е. Обозначение: ln x = loge x . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Пользуясь вычисленным пределом, докажем несколько эквивалентностей: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
lim ln(1 + x) |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1. |
= lim |
|
|
|
|
=1 |
|
ln(1+ x) ~ |
x |
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
−1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
x→0 |
|
x |
|
y→0 ey |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
loga (1 + x) |
|
|
|
|
|
|
|
ln(1+x) |
|
|
|
ln(1 + x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2. |
lim |
= lim |
|
|
ln a |
|
= lim |
|
=1 |
|
|
|
|
|
loga (1 + x) ~ |
x |
|
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x→0 |
|
|
|
x |
|
|
|
|
|
x→0 |
x |
|
|
|
|
x→0 |
|
x |
|
|
|
|
|
|
|
|
|
x→0 ln a |
|
||||||||||||||||
|
|
|
ln a |
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ах −1 = lim ex ln a −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3. |
lim |
=1 |
a x −1 |
|
~ x ln a |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x→0 |
хln a |
x→0 |
|
xln a |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
4. lim |
(1+ x)a −1 |
= lim |
ea ln(1+x) |
−1 |
|
= lim |
a ln(1+ x) |
= lim |
ax |
|
=1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ax |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x→0 |
|
ax |
|
|
|
x→0 |
|
|
|
|
|
ax |
|
|
|
|
|
x→0 |
|
ax |
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|||||||||||||
|
(1 + x)a −1 |
~ |
|
ax |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
ln(1+x) |
|
lim |
ln(1+x) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
5. |
lim(1 + x) |
x |
= limeln(1+x)x |
= limex |
|
|
|
|
|
= e x→0 |
x |
= e . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
x→0 |
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из последнего соотношения можно вывести: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
lim 1 + |
x |
|
|
|
= lim(1 + y)y = e – второй замечательный предел. |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
x→∞ |
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Полученные соотношения эквивалентности можно внести в таблицу. Этой таблицей пользуются при выделении главных частей б.м. и б.б. функций, а также при вычислении пределов.
Таблица 2.1.1.. Таблица эквивалентных бесконечно малых
1 |
sin x |
~ |
x |
5 |
|
1 |
−cos x |
~ |
x2 |
|||
|
|
x→0 |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
x→0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
2 |
tg x |
~ |
x |
6 |
|
loga (1 + x) |
~ |
x |
|
ln(1 + x) ~ x |
||
|
|
|||||||||||
|
x→0 |
|
|
|
x→0 ln a |
|
|
x→0 |
||||
|
|
|
|
|
20 |
|
|
|
|
|
|
|