Раздел 4. Основы цифровой и микропроцессорной техники

Логические функции. Описание логических функций с помощью таблиц истинности. Базовые логические функции. Логические вентили ТТЛ, ТТЛШ, МОП и КМОП структур; вентили с тремя состояниями.

Триггеры на логических элементах: RS,JK,Dи Т триггеры. Системы счисления. Счетчики импульсов. Микроконтроллеры: принципы организации микропроцессоров; архитектура микропроцессоров и их функционирование, структура микроконтроллеров.

Самостоятельное изучение: описание логических функций с помощью таблиц истинности; реализация триггеров на логических элементах: RS, JK, D и Т триггеры. двоичная и шестнадцатеричная системы счисления; преобразование из десятичной системы счисления в двоичную и шестнадцатеричную системы счисления и наоборот.

Лекция 7.

7.1. Логические функции. Описание логических функций с помощью таблиц истинности. Базовые логические функции.

Логические функции. Логической функцией называется функция, которая как и ее переменные может принимать только два значения – ноль или единицу. Логическая величина характеризует два взаимоисключающих понятия: есть и нет, включено и выключено и т.п. Если одно из значений логической величины обозначено через х, то второе обозначают через(не х). Логические функции выражают зависимость выходных переменных от входных. Эти функции, в зависимости от числа входных переменных, делятся на функции одной, двух или многих переменных. Логические функции и логические операции над ними – предмет алгебры логики (булевой алгебры).

Для операций с логическими выражениями используются законы алгебры логики. В качестве примера, приведем некоторые из часто используемых.

Закон нулевого множества:

0 + а = а; 0 · а = 0; 0· а ·в … · i= 0.

Закон универсального множества:

1 · а = а; 1 + а = 1; 1 + а + в … ·+i= 1.

Закон идемпотентности (повторения, тавтологии):

а ∙ а = а; а ∙ а…∙ а = аⁿ; а + а = а; а + а…+ а = а.

З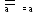акон двойной инверсии:

Законы дополнительности:

- логическое противоречие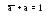

- закон исключенного третьего

Дистрибутивные (распределительные) законы:

а (в + с) = ав + ас; а + в с = (а + в) (а + с).

Законы поглощения:

а (а + в) = а; а (а + в) (а + с) = а; а + а ∙ в + а ∙ с …+ а ∙ w= а.

З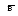аконы склеивания(распространения):

а ∙ в + а = а; (а + в) (а + ) = а.

Закон Де Моргана:

Другой способ определения логических функций основывается на задании логической функции с помощью таблицы истинности путем сопоставления каждому набору входных переменных определенного значения функции – логического нуля или логической единицы. Различные комбинации значений входных переменных в логических функциях называются наборами. Функция является полностью заданной, если указаны её значения на всех её наборах. Число наборовmдляnвходных переменных определяется выражениемm = 2ⁿ .

В таблице 6.1 в качестве примера показано задание логической функции fот двух логических переменныхаив.

		Таблица 6.1
а	в	f (a, b)
0	0	0
0	1	1
1	0	1
1	1	1

Базовые логические функции.

В булевой алгебре над переменными могут производиться три основных действия:

1. Логическое сложение — дизъюнкцияили функция ИЛИ: y = x₁+ x₂ или

y = x₁Vx_{2 .} Эта функция определяется так: y = 1, если x₁= 1 или x₂= 1, а также если

x₁= 1 и x₂= 1.

2. Логическое умножение — конъюнкцияили функция И: y = x₁· x₂или

y = x₁^ x₂Определяется так: y = 1, если толькоодновременноx₁= 1 и x₂= 1.

3. Логическое отрицание — инверсияили функция НЕ: если понятие «не x» обозначить буквой y, то y =.

Сочетание функций ИЛИ и И с инверсией приводит дополнительно еще к двум комбинированным функциям:

1. Функция отрицания логического сложения ИЛИ-НЕ: y = x₁+ x₂. Второе название - «стрелка Пирса» -y=x₁↓x₂.

2. Функция отрицания логического произведения И-НЕ: y = x₁∙ x₂. Второе название «штрих Шеффера»y=x₁∕x₂.

Последние две функции — самые распространенные, так как на их основе можно реализовать любуюлогическую функцию, в том числе и простейшие – ИЛИ, И, НЕ.

Кроме рассмотренных логических функций к базовым функциям можно отнести еще ряд функций, появление которых связано с развитием цифровой и микропроцессорной техники. Такой функцией, например, является логическая функция «исключающая ИЛИ». По другому – «сумма по модулю два» (сумма по mod2). Эта логическая функция находит применение в микропроцессорной технике для построенияn–разрядных сумматоров для проведения операций математического сложения и вычитания.

На рис. 7.1 приведено условное графическое обозначение базовых логических функций, а в таблице 7.2 – таблица истинности рассмотренных логических функций.

					Таблица 7.2.
x1	x2	y
		ИЛИ	И	ИЛИ-НЕ		И-НЕ	искл.ИЛИ
0	0	0	0	1		1	0
0	1	1	0	0		1	1
1	0	1	0	0		1	1
1	1	1	1	0		0	0