,

где x₁ = 1 - x.

Таким образом заполняются столбцы 3, 4 и 5 таблицы 2.6. В столбце 6 записываются ординаты линии влияния М₂, подсчитан­ные по формуле (2.41). На рис. 2.25, д приведена линия влияния М₂.

Для построения линий влияния изгибающих моментов и попе­речных сил в сечении неразрезной балки используются зависи­мости:

; (2.43)

(2.44)

где и- ординаты эпюр М_k и Q_k от внешней нагрузки в се­чении к балки пролетом l_n на двух шарнирных опорах; M_n и M_n-1 - линии влияния опорных моментов неразрезной балки.

Ординаты линии влияния опорной реакции R_n подсчитываются по формуле:

, (2.45)

где - линия влияния реакции шарнирной балки n, если эту эпюру рассматривать как общую для двух простых балок пролетом l_n и l_n+1.

На рис. 2.23, е, ж приведены линии влияния опорных реакций R₂ и для неразрезной балки, приведенной на рис. 2.23,а.

2.11. Расчет неразрезной балки на действие постоянных и временных нагрузок (задача 9)

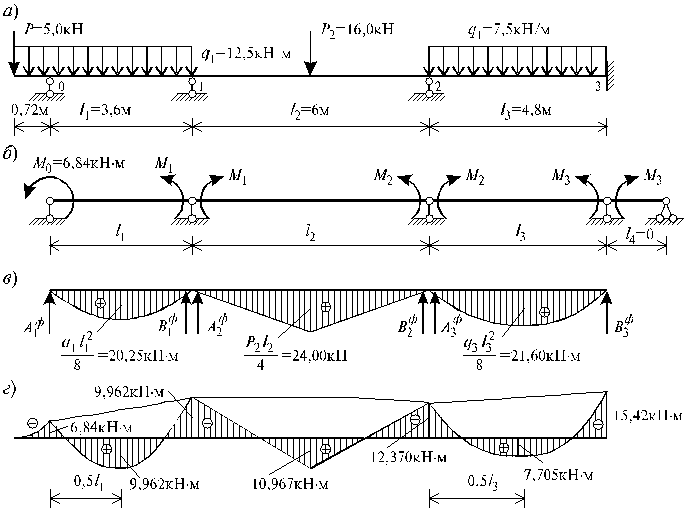
Для неразрезной балки постоянного поперечного сечения (рис. 2.26, а) требуется:

1. Построить эпюру изгибающих моментов от заданной посто­янной нагрузки с помощью уравнений трех моментов;

2. Построить линии влияния опорных изгибающих моментов М₁, М₂ и изгибающего момента в сечении, расположенном посере­дине пролета l₂ ;

3. По линиям влияния, полученным в п. 2 проверить ординаты эпюры М, полученной в п. 1;

4. От временной равномерно распределенной нагрузки интен­сивностью q = 10 кН/м (может располагаться с разрывами в не­скольких і пролетах балки) и заданной постоянной нагрузки по­строить объемлющую эпюру изгибающих моментов для пролета l₂.

Решение

1. Построение эпюры изгибающих моментов

Для составления уравнений трех моментов получим основную систему путем введения в заданную неразрезную балку шарниров над всеми промежуточными опорами, предварительно заменив за­делку дополнительным пролетом длиной l₄ =0.  Кроме того, заме­ним консоль с нагрузкой внешним сосредоточенным моментом М₀. Полученная основная система показана на рис. 2.26, б. Напишем уравнения трех моментов для промежуточных опор:

(2.46)

В этих уравнениях: M₀ = -5.0×0.72 -= 6.84 кН×м; M₄ = = 0; l₄ = 0.

Построим эпюру изгибающих моментов в основной системе от заданной внешней нагрузки. Она представляет собой сочетание эпюр изгибающих моментов для всех пролетов балки, если каждый из них рассматривать как балку на двух шарнирных опорах. Указанная эпюра показана на рис. 2.26, в. Используя эту эпюру, найдем фиктивные опорные реакции (увеличенные в EJ раз) для каждого пролета балки:

кН×м²;

кН×м²;

кН×м²;

.

Рис. 2.26

Подставляя все известные числовые величины в систему урав­нений (2.46), получим:

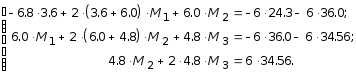
После несложных преобразований получим:

(2.47)

Умножив обе части второго уравнения на 2 и вычитая третье уравнение, получим:

12.0 M₁ + 38.4 M₂ = -639.36.

Учитывая первое уравнение системы (2.47), получим:

(2.48)

Решая полученную систему (2.7.3), найдем:

M₁ = -13.696 кН×м;    M₂ = -12.370 кН×м.

Подставляя значение М₂ в третье уравнение системы (2.47), найдем:

М₃ = -15.420 кН×м.

Для проверки решения подставим найденные величины М₁, М₂ и М₃  в каждое из уравнений системы (2.47):

Результаты проверки подтверждают правильность нахождения неизвестных М₁, М₂ и М₃ . По полученным данным построим эпю­ру опорных моментов (на рис. 2.26, г показана пунктиром). Отло­жив от пунктирной линии ординаты эпюры изгибающих моментов в основной системе, которая показана на рис. 2.26, в, получим эпюру изгибающих моментов от постоянной внешней нагрузки для заданной неразрезной балки (рис. 2.26, г).

2. Построение линий влияния опорных моментов м1 и м2 и изгибающего момента в сечении, расположенном посередине пролета l2

Согласно общей методике, изложенной в п. 2.10, для построе­ния линий влияния М₁ кинематическим методом, необходимо в балке нарушить ту связь, которая передает это усилие, и заменить нарушенную связь моментом М₁ .

Изобразив, примерный вид упругой линии основной системы от усилия М₁ = 1, получим модель линии влияния момента М₁ .

Запишем систему уравнений трех моментов (исключая для опо­ры 1) для определения изгибающих моментов на опорах от дейст­вия М₁ = 1:

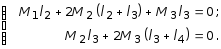
Учитывая, что l₄ = 0, а М₁ = 1, получим:

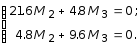
Из второго уравнения имеем: М₂ = -2М₃.

Подставим это значение в первое уравнение получим:

21.6×(-2М₃) + 4.8M₃ + 6 = 0, откуда кН×м. Далее кН×м.

    По данным рис. 2.23 подсчитаем взаимный угол поворота смеж­ных сечений основной системы на опоре 1: 

Расчеты будем вести в табличной форме (табл. 2.7, где ордина­ты линии влияния умножены на число EJ).

Таблица 2.7

Часть балки	Сече­ние	Момент на опоре при­ложен слева	Момент на опоре при­ложен справа	Момент на опоре приложен и слева и справа	Ординаты линии влияния, М1
Пролет 0-1	0 0.25 0.50 0.75 1.0	0 0 0 0 0	0 0.4925 0.7776 0.6739 0	0 0.4925 0.7776 0.6739 0	0 0.17533 0.28050 0.24542 0
Пролет 1-2	0 0.25 0.50 0.75 1.0	0 1.8720 2.1600 1.7280 0	0 -0.5400 -0.6750 -0.5850 0	0 1.3320 1.4850 1.1430 0	0 0.52927 0.53543 0.27386 0
Пролет 2-3	0 0.25 0.50 0.75 1.0	0 -0.3744 -0.4320 -0.2736 0	0 0.1728 0.2160 0.1872 0	0 -0.2016 -0.2160 -0.0864 0	0 0.08773 0.07800 -0.02927 0

Аналогично строим линию влияния опорного момента М₂. За­пишем систему уравнений трех моментов (исключая для опоры 2) для определения изгибающих моментов на опорах от действия М₂ = 1:

Учитывая, что l₄ = 0, а M₂ = 1, получим:

Решив эту систему, получим:

кН×м;    кН×м.

Взаимный угол поворота смежных сечений основной системы на опоре 2:

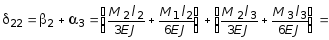
Расчеты будем вести в табличной форме (табл. 2.8, где ордина­ты линии влияния умножены на число EJ).

Таблица 2.8

Часть балки	Сече­ние	Момент на опоре прило­жен слева	Момент на опоре прило­жен справа	Момент на опоре приложен и слева и справа	Ординаты линии влияния, М2
Пролет 0-1	0 0.25 0.50 0.75 1.0	0 0 0 0 0	0 -0.1368 -0.2160 -0.1872 0	0 -0.1368 -0.2160 -0.1872 0	0 -0.05465 -0.08775 -0.07678 0
Пролет 1-2	0 0.25 0.50 0.75 1.0	0 -0.3120 -0.3600 -0.2280 0	0 1.3680 2.1600 1.8720 0	0 1.0560 1.8000 1.6440 0	0 0.27386 0.53643 0.52927 0
Пролет 2-3	0 0.25 0.50 0.75 1.0	0 1.1980 1.3824 0.8755 0	0 -0.4378 -0.6912 -0.5990 0	0 0.7602 0.6912 0.2765 0	0 0.26050 0.24938 0.09357 0

Ординаты линии влияния изгибающего момента в сечении, расположенном посередине второго пролета , определяем по формуле:

,

где - ординаты линии влияния изгибающего момента в сече­нии, расположенном посередине второго пролета, если этот пролет рассматривать как балку на двух шарнирных опорах; M₁ и M₂ - ор­динаты линий влияния опорных моментов M₁ и M₂ .

По полученным данным строим линии влияния опорных изги­бающих моментов M₁ и M₂ , а также линию влияния изгибающего момента (см. рис. 2.27).

Для дальнейших расчетов подсчитаем методом трапеций пло­щади линий влияния М₁, М₂  и для каждого из пролетов.

Линия влияния М₁:

м²;

м²;

м²;

м².

Линия влияния М₂:

м²;

м²;

м²;

м².

Линия влияния :

м²;

м²;

м²;

м².